Với giải Luyện tập 2 trang 107 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 3: Tiếp tuyến của đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 3: Tiếp tuyến của đường tròn
Luyện tập 2 trang 107 Toán 9 Tập 1: Cho đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại điểm I. Gọi d là tiếp tuyến của (O; R) tại điểm I. Chứng minh d là tiếp tuyến của (O’; R’).
Lời giải:
Vì đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại điểm I nên ba điểm O, I, O’ thẳng hàng và I nằm giữa O và O’.
Vì đường thẳng d là tiếp tuyến của đường tròn (O; R) tại I nên d ⊥ OI tại I.
Do đó d ⊥ O’I tại I, mà I thuộc đường tròn (O’; R’) nên d là tiếp tuyến của (O’; R’).
Lý thuyết Nhận biết tiếp tuyến của đường tròn
Nhận xét: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.
Dấu hiệu nhận biết tiếp tuyến
|
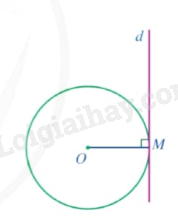
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn. |
Xem thêm lời giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
§2. Vị trí tương đối của đường thẳng và đường tròn
§5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
§1. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
