Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 9 Tiếp tuyến của đường tròn được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Tiếp tuyến của đường tròn. Mời các bạn đón xem:

Bài tập Toán 9 Tiếp tuyến của đường tròn

A. Bài tập Tiếp tuyến của đường tròn

Bài 1. Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA, MB là hai tiếp tuyến (A, B là hai tiếp điểm). Biết $\widehat{MAB}=70°,$ số đo $\widehat{AOM}$ bằng

A. 70°;

B. 140°;

C. 35°;

D. 110°.

Hướng dẫn giải

Đáp án đúng là: A

Ta có AM là tiếp tuyến của (O) tại A nên AM ⊥ OA.

Do đó $\widehat{OAB}+\widehat{BAM}=90°.$

Vì vậy $\widehat{OAB}=90°-\widehat{BAM}=90°-70°=20°.$

Ta có tam giác OAB cân tại O (do OA = OB = R) nên $\widehat{OBA}=\widehat{OAB}=20°.$

Tam giác OAB, có: $\widehat{AOB}+\widehat{OBA}+\widehat{OAB}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{AOB}=180°-\left(\widehat{OBA}+\widehat{OAB}\right)=180°-\left(20°+20°\right)=140°.$

Ta có MA, MB là hai tiếp tuyến của đường tròn (O) nên OM là tia phân giác của $\widehat{AOB}$ (tính chất hai tiếp tuyến cắt nhau).

Do đó $\widehat{AOM}=\frac{\widehat{AOB}}{2}=\frac{140°}{2}=70°.$

Vậy ta chọn phương án A.

Bài 2. Cho đường tròn (O; R). Từ một điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm) sao cho $\widehat{AMO}=30°.$

a) Chứng minh MO = 2R;

b) Tính AB theo R.

Hướng dẫn giải

Theo đề bài, ta có hình vẽ sau:

a) Xét ∆OAM có

Ta có $\sin \widehat{AMO}=\frac{OA}{OM}=\sin 30°=\frac{1}{2}$  suy ra OM = 2R.

b) Vì MA, MB là tiếp tuyến của (O) suy ra MA = MB.

Mà MO là tia phân giác của góc $\widehat{AMB}$ (tính chất hai tiếp tuyến cắt nhau).

Suy ra ∆MAB cân tại M, $\widehat{AMB}=2\widehat{AMO}=60°.$

Do đó AMB là tam giác đều, suy ra AB = AM.

Xét ∆OAM có $\widehat{OAM}=90°$ suy ra AM² = OM² – OA² (theo định lí Pythagore).

Vậy $AM=R\sqrt{3}=AB.$

Bài 3. Trong hình sau, AB = 6, BC = 6, AC = 10 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).

Hướng dẫn giải

Ta có: AB = 6, BC = 8, AC = 10 suy ra AC² = AB² + BC² nên tam giác ABC vuông tại B hay $\widehat{ABC}=90°.$  Suy ra AB ⊥ BC.

Mà O ∈ BC nên AB ⊥ BO.

Vậy AB đi qua B (B ∈ (O)) và AB ⊥ BO = R nên AB là tiếp tuyến của đường tròn (O).

Bài 4. Cho đường tròn tâm O, bán kính R. Từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC với đường tròn tâm O với B, C là tiếp điểm.

a) Chứng minh AO là đường trung trực của BC;

b) Kẻ đường kính CD của (O). Chứng minh BD song song với AO;

c) Kẻ OM vuông góc với OB (M thuộc AC). Chứng minh MO = MA.

Hướng dẫn giải

Theo đề bài, ta có hình vẽ sau:

a) Vì AB, AC là tiếp tuyến của (O) suy ra AC = AB (tính chất hai tiếp tuyến cắt nhau).

Suy ra A thuộc đường trung trực của BC.

Mặt khác OA = OB (cùng bằng bán kính) suy ra O thuộc đường trung trực của BC.

Do đó AO là đường trung trực của BC.

b) Vì BO là đường trung tuyến của ∆DBC, $BO=\frac{1}{2}CD.$

Suy ra ∆DBC vuông tại B hay BD ⊥ BC.

Mặt khác AO ⊥ BC (do AO là trung trực của BC) suy ra AO // BD.

c) Vì OM ⊥ OB suy ra $\widehat{MOA}+\widehat{AOB}=90°.$  (1)

Ta có $\widehat{MAO}=\widehat{BAO}$  (vì A là giao điểm của hai tiếp tuyến chung của (O)).

Vì $\widehat{OAB}+\widehat{AOB}=90°$  suy ra $\widehat{MAO}+\widehat{AOB}=90°.$  (2)

Từ (1) và (2) suy ra $\widehat{MAO}=\widehat{MOA}$  suy ra ∆AMO cân tại M hay MA = MO.

Bài 5. Cho đường tròn (O; R). Từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC với đường tròn (O), với B, C là tiếp điểm.

a) Chứng minh AO là đường trung trực của đoạn BC.

b) Kẻ đường kính CD của (O). Chứng minh BD // AO.

c) Kẻ OM vuông góc với OB (M thuộc AC). Chứng minh MO = MA.

Hướng dẫn giải

Vì AB, AC là tiếp tuyến của (O) nên AB = AC (tính chất hai tiếp tuyến cắt nhau)

Suy ra A thuộc đường trung trực của đoạn BC (1)

Lại có OA = OB = R.

Suy ra O thuộc đường trung trực của đoạn BC (2)

Từ (1), (2), ta thu được OA là đường trung trực của đoạn BC.

b) Tam giác BCD có OB = OC = OD = R và O là trung điểm CD (do CD là đường kính của (O)).

Do đó tam giác BCD vuông tại B hay BD ⊥ BC.

Mà AO ⊥ BC (do OA là đường trung trực của đoạn BC)

Vậy AO // BD.

c) Ta có OM ⊥ OB nên $\widehat{MOA}+\widehat{AOB}=90°$ (3)

Ta có AB, AC là hai tiếp tuyến của (O) nên AO là tia phân giác của $\widehat{BAC}$.

Do đó $\widehat{MAO}=\widehat{OAB}$ (4)

Ta có tam giác OAB vuông tại B (do AB là tiếp tuyến của (O)).

Suy ra $\widehat{AOB}+\widehat{OAB}=90°$ (5)

Từ (3), (4), (5), ta thu được $\widehat{MAO}=\widehat{MOA}.$

Do đó tam giác AMO cân tại M.

Vậy MA = MO.

B. Lý thuyết Tiếp tuyến của đường tròn

1. Vị trí tương đối của đường thẳng và đường tròn

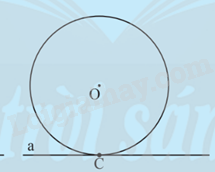
Đường thẳng a và đường tròn (O) có duy nhất một điểm chung C thì ta nói a tiếp xúc với (O) tại C, khi đó a là tiếp tuyến của đường tròn (O) tại C và C là tiếp điểm.

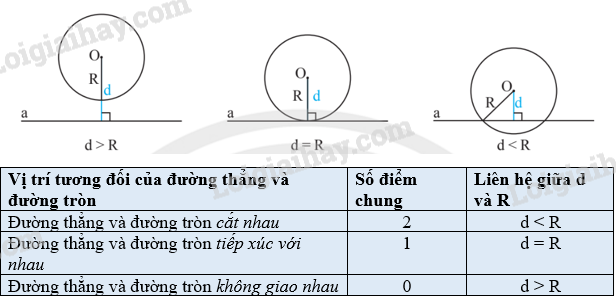
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Dấu hiệu nhận biết tiếp tuyến

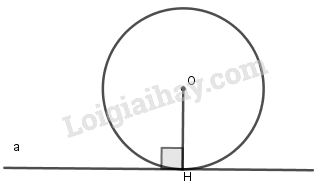
Tính chất của tiếp tuyến

3. Tính chất của hai tiếp tuyến cắt nhau

Định lí

Ví dụ: Cho đường tròn (O), B, C $\in$ (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.

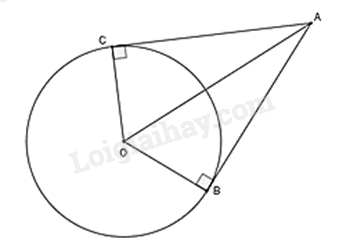
Khi đó:

- AB = AC

- Tia AO là tia phân giác của $\widehat{BAC}$.

- Tia OA là tia phân giác của $\widehat{BOC}$.

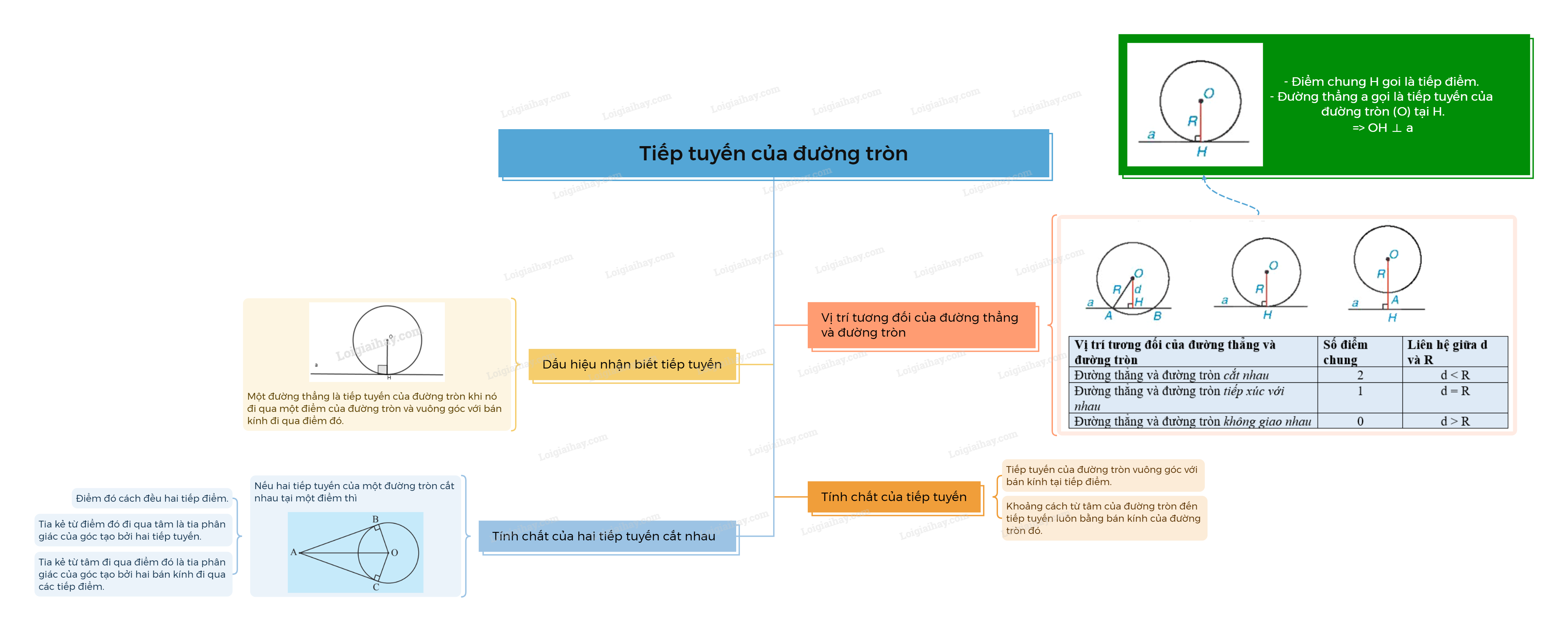
Sơ đồ tư duy Tiếp tuyến của đường tròn