Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn

Khởi động trang 101 Toán 9 Tập 1: Vị trí của Mặt Trời so với đường chân trời (Hình 19) gợi nên hình ảnh vị trí tương đối của đường thẳng và đường tròn.

Làm thế nào để xác định được vị trí tương đối của đường thẳng và đường tròn?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

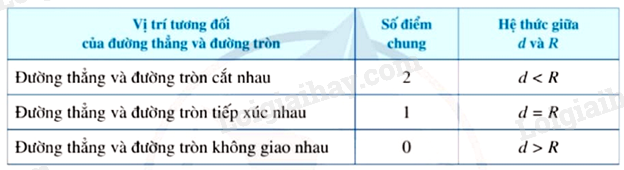
Ta có thể nhận biết vị trí tương đối của đường thẳng a và đường tròn (O; R) thông qua hệ thức giữa khoảng cách d từ tâm O đến đường thẳng a và bán kính R như bảng sau:

Hoạt động 1 trang 101 Toán 9 Tập 1: Quan sát Hình 20.

a) Cho biết đường thẳng a và đường tròn (O; R) có bao nhiêu điểm chung.

b) So sánh độ dài đoạn thẳng OH và R.

Lời giải:

a) Đường thẳng a và đường tròn (O; R) có 2 điểm chung.

b) Ta có OH và OM lần lượt là đường vuông góc và đường xiên kẻ từ O đến đường thẳng a.

Do đó OH < OM hay OH < d.

1. Đường thẳng và đường tròn cắt nhau

Luyện tập 1 trang 102 Toán 9 Tập 1: Hãy chỉ ra một số hiện tượng trong thực tiễn gợi nên hình ảnh của đường thẳng và đường tròn cắt nhau.

Lời giải:

Một số hiện tượng trong thực tiễn gợi nên hình ảnh của đường thẳng và đường tròn cắt nhau: biển báo giao thông (chẳng hạn biển cấm đường), đĩa có họa tiết kẻ caro, …

2.Đường thẳng và đường tròn tiếp xúc nhau

Hoạt động 2 trang 102 Toán 9 Tập 1: Trong bức ảnh ở Hình 22, đường ray và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?

Lời giải:

Đường thẳng và đường tròn đó có 1 điểm chung.

Luyện tập 2 trang 102 Toán 9 Tập 1: Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Đường thẳng AB có tiếp xúc với đường tròn (C; 4 cm) hay không? Vì sao?

Lời giải:

Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC²

Suy ra AC² = BC² – AB² = 5² – 3² = 16.

Do đó AC = 4 cm (do AC > 0).

Vì CA ⊥ AB tại A nên khoảng cách từ điểm C đến đường thẳng AB bằng CA.

Mà AC = 4 cm nên khoảng cách từ tâm C của đường tròn (C; 4 cm) đến đường thẳng AB bằng bán kính của đường tròn.

Vậy đường thẳng AB tiếp xúc với đường tròn (C; 4 cm).

3. Đường thẳng và đường tròn không giao nhau

Hoạt động 3 trang 103 Toán 9 Tập 1: Trong Hình 25, cột thẳng đứng và biển quảng cáo có dạng hình tròn gợi nên hình ảnh của đường thẳng và đường tròn không giao nhau. Theo em, đường thẳng và đường tròn không giao nhau thì chúng có điểm chung hay không?

Lời giải:

Đường thẳng và đường tròn không giao nhau thì chúng không có điểm chung.

Hoạt động 4 trang 103 Toán 9 Tập 1: Quan sát Hình 26.

a) Cho biết đường thẳng a và đường tròn (O; R) có bao nhiêu điểm chung.

b) So sánh độ dài đoạn thẳng OH và R.

Lời giải:

a) Đường thẳng a và đường tròn (O; R) không có điểm chung.

b) OH > R.

Luyện tập 3 trang 104 Toán 9 Tập 1: Cho điểm O và đường thẳng a thỏa mãn khoảng cách từ O đến đường thẳng a bằng 4 cm. Xác định vị trí tương đối của đường thẳng a và các đường tròn (O; 3 cm), (O; 4 cm), (O; 5 cm).

Lời giải:

– Vì 4 > 3 nên khoảng cách từ O đến đường thẳng a lớn hơn bán kính của đường tròn (O; 3 cm). Vậy đường thẳng a và đường tròn (O; 3 cm) không giao nhau.

– Vì khoảng cách từ O đến đường thẳng a bằng bán kính của đường tròn (O; 4 cm). Vậy đường thẳng a và đường tròn (O; 4 cm) tiếp xúc nhau.

– Vì 4 < 5 nên khoảng cách từ O đến đường thẳng a nhỏ hơn bán kính của đường tròn (O; 5 cm). Vậy đường thẳng a và đường tròn (O; 5 cm) cắt nhau.

Bài tập

Bài 1 trang 104 Toán 9 Tập 1: Đồng hồ treo tường trang trí ở Hình 29 gợi nên vị trí tương đối của đường thẳng và đường tròn.

Quan sát Hình 29 và chỉ ra một hình ảnh đường thẳng và đường tròn:

a) Cắt nhau;

b) Tiếp xúc nhau;

c) Không giao nhau.

Lời giải:

a) Đường thẳng màu đen cắt đường tròn màu cam.

b) Đường thẳng màu đen tiếp xúc với đường tròn màu xanh mạ non.

c) Đường thẳng màu vàng không giao nhau với đường tròn màu đỏ.

Bài 2 trang 104 Toán 9 Tập 1: Trong Hình 30, mép ngoài cửa ra vào có dạng một phần của đường tròn bán kính 1,6 m. Hãy tính chiều cao HK của cửa đó (làm tròn kết quả đến hàng phần mười của mét), biết AH = 0,9 m.

Lời giải:

Xét ∆OAH vuông tại H, theo định lý Pythagore ta có:

OA² = OH² + AH²

Suy ra OH² = OA² – AH² = 1,6² – 0,9² = 1,75.

Do đó OH = $\sqrt{1,75}=\sqrt{\frac{7}{4}}=\frac{\sqrt{7}}{2}\text{(m).}$

Khi đó, HK = OH + OK = $\frac{\sqrt{7}}{2}+1,6\approx$2,9 (m).

Vậy chiều cao của cửa là khoảng 2,9 mét.

Bài 3 trang 104 Toán 9 Tập 1: Trên mặt phẳng, một vật nhỏ chuyển động trên đường tròn tâm O bán kính 2 m, một vật khác chuyển động trên đường thẳng a sao cho khoảng cách từ điểm O đến đường thẳng a bằng 3 m. Hai vật nhỏ có bao giờ gặp nhau không?

Lời giải:

Vì 3 > 2 nên khoảng cách từ O đến đường thẳng a lớn hơn bán kính của đường tròn (O; 2 m).

Vậy đường thẳng a và đường tròn (O; 2 m) không giao nhau nên hai vật nhỏ không bao giờ gặp nhau.

Bài 4 trang 105 Toán 9 Tập 1: Cho bốn điểm O, M, N, P cùng nằm trên một đường thẳng sao cho điểm M nằm giữa hai điểm O và N; điểm N nằm giữa hai điểm M và P. Gọi a, b, c lần lượt là các đường thẳng đi qua M, N, P và vuông góc với đường thẳng OP. Xác định vị trí tương đối của mỗi đường thẳng a, b, c và đường tròn (O; ON).

Lời giải:

– Vì điểm M nằm giữa hai điểm O và N nên OM < ON suy ra khoảng cách từ O đến đường thẳng a nhỏ hơn bán kính của đường tròn (O; ON). Vậy đường thẳng a và đường tròn (O; ON) cắt nhau.

– Vì khoảng cách từ O đến đường thẳng b (là ON) bằng bán kính của đường tròn (O; ON). Vậy đường thẳng b và đường tròn (O; ON) tiếp xúc nhau.

– Vì điểm M nằm giữa hai điểm O và N; điểm N nằm giữa hai điểm M và P nên điểm N nằm giữa hai điểm O và P.

Suy ra OP > ON nên khoảng cách từ O đến đường thẳng c lớn hơn bán kính của đường tròn (O; ON). Vậy đường thẳng b và đường tròn (O; ON) không giao nhau.

Bài 5 trang 105 Toán 9 Tập 1: Cho điểm O và đường thẳng a không đi qua O.

a) Vẽ điểm H là hình chiếu của điểm O trên đường thẳng a.

b) Từ đó, vẽ ba đường tròn tâm O lần lượt: không giao với đường thẳng a; tiếp xúc với đường thẳng a; cắt đường thẳng a tại hai điểm phân biệt.

Lời giải:

a)

b)

Đường tròn (O; OM) không giao với đường thẳng a;

Đường tròn (O: OH) tiếp xúc với đường thẳng a;

Đường tròn (O; OK) cắt đường thẳng a tại hai điểm A và B phân biệt.

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

§1. Đường tròn. Vị trí tương đối của hai đường tròn

§2. Vị trí tương đối của đường thẳng và đường tròn

§3. Tiếp tuyến của đường tròn

§4. Góc ở tâm. Góc nội tiếp

§5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên

Bài tập cuối chương 5

Lý thuyết Vị trí tương đối của đường thẳng và đường tròn

1. Đường thẳng và đường tròn cắt nhau

Nếu đường thẳng và đường tròn cắt nhau thì mỗi điểm chung được gọi là một giao điểm.

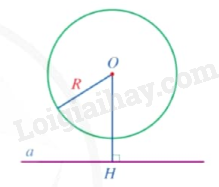
Nhận xét: Đường thẳng a cắt đường tròn (O;R) khi khoảng cách từ tâm O đến đường thẳng a nhỏ hơn R và ngược lại.

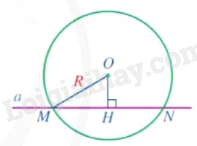
2. Đường thẳng và đường tròn tiếp xúc nhau

Nếu đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn, điểm chung được gọi là tiếp điểm.

Nhận xét: Đường thẳng a tiếp xúc với đường tròn (O;R) khi khoảng cách từ tâm O đến đường thẳng a bằng R và ngược lại.

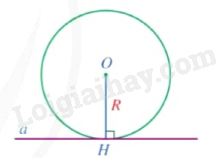
3. Đường thẳng và đường tròn không giao nhau

Nhận xét: Đường thẳng a và đường tròn (O;R) không giao nhau khi khoảng cách từ tâm O đến đường thẳng a lớn hơn R và ngược lại.

Nhận xét: Ta có thể nhận biết vị trí tương đối của đường thẳng a và đường tròn (O;R) thông qua hệ thức giữa khoảng cách d từ tâm O đến đường thẳng a và bán kính R được tóm tắt trong bảng sau: