Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
Khởi động trang 118 Toán 9 Tập 1: Hình 65 mô tả một chiếc quạt giấy.
Hình phẳng được tô màu đỏ ở Hình 65 được gọi là hình gì và diện tích của hình đó được tính như thế nào?
Lời giải:
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Hình phẳng được tô màu đỏ ở Hình 65 được gọi là hình quạt tròn (hình quạt), hình này là một phần hình tròn giới hạn bởi cung tròn AB và hai bán kính OA, OB.
Giả sử hình quạt tròn AOB, tâm O, bán kính R và cung tương ứng với hình quạt có số đo n°.
Diện tích của hình quạt đó là: (đơn vị diện tích).
Đo chiều dài sợi dây đó.
Ta nói chiều dài sợi dây bằng chu vi của đường tròn.
Lời giải:
HS thực hiện hoạt động theo hướng dẫn của GV và SGK.
Lời giải:
Chu vi của đường tròn là: C = 2π.5 = 10π ≈ 31,4 (cm).
1. Độ dài cung tròn
Đo chiều dài sợi dây đó.
Ta nói chiều dài sợi dây bằng độ dài của cung tròn AB.
b) Ta coi mỗi đường tròn bán kính R là một cung tròn có số đo 360°. Chia đường tròn đó thành 360 phần bằng nhau, mỗi phần là cung tròn có số đo bằng 1°; chu vi của đường tròn khi đó cũng được chia thành 360 phần bằng nhau. Tính theo R:
⦁ Độ dài của cung có số đo 1°;
⦁ Độ dài của cung có số đo n°.
Lời giải:
a) HS thực hiện hoạt động theo hướng dẫn của GV và SGK.
b) Độ dài của cung tròn có số đo 360° chính là chu vi của đường tròn bán kính R và bằng 2πR.
Độ dài của cung có số đo 1° là:
Độ dài của cung có số đo n° là
Lời giải:
Ta có là số đo của cung AB.
Độ dài quãng đường AB mà con lắc đó đã di chuyển là:
2. Diện tích hình quạt tròn
Lời giải:
Ta có:
⦁ OA < 2 cm nên A nằm trong đường tròn (O; 2 cm);
⦁ OB = 2 cm nên B nằm trên đường tròn (O; 2 cm).
Lời giải:
Phần hình tròn (O) tô màu xanh được giới hạn bởi hai bán kính OA, OB và cung AmB.
Lời giải:
Xét ∆OCD có OC = OD = CD nên ∆OCD là tam giác đều, do đó
Vì góc COD là góc ở tâm chắn cung nhỏ CD nên
Do đó
a) 1°;
b) n° (Hình 75).
Lời giải:
a) Diện tích của hình tròn bán kính R là S = πR2.
Cả đường tròn có số đo là 360° nên diện tích hình quạt tròn tâm O, bán kính R cung số đo 1° là:
b) Diện tích hình quạt tròn tâm O, bán kính R cung số đo n° là:
a) Tính diện tích của hình quạt đó.
b) Tính chiều dài cung tương ứng với hình quạt tròn đó.
Lời giải:
a) Diện tích hình quạt đó là:
b) Ta có suy ra
Vậy độ dài cung tương ứng với hình quạt tròn đó là:
3. Diện tích hình vành khuyên
b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn (O; 2 cm) và (O; 3 cm). Tính hiệu diện tích của hai hình tròn đó.
Lời giải:
a) Hình chi tiết máy được giới hạn bởi hai đường tròn cùng tâm.
b)
Diện tích hình tròn tâm O bán kính 3 cm là: π.32 = 9π (cm2).
Diện tích hình tròn tâm O bán kính 2 cm là: π.22 = 4π (cm2).
Hiệu diện tích của hai hình tròn đó là: 9π – 4π = 5π (cm2).
Lời giải:
Hình vành khuyên giới hạn bởi hai đường tròn cùng tâm O và có bán kính lần lượt là 2,5 cm; 2 cm được tô màu xanh như hình vẽ dưới đây:
Diện tích của hình vành khuyên tô màu xanh là:
Bài tập
Bài 1 trang 122 Toán 9 Tập 1: Quan sát các hình 83, 84, 85, 86.
a) Tính diện tích phần được tô màu mỗi hình đó.
b) Tính độ dài cung tròn được tô màu xanh ở mỗi hình 83, 84.
Lời giải:
a) ⦁ Hình 83: Diện tích hình quạt tròn có bán kính 2 cm, số đo cung 40° là:
Vậy diện tích phần được tô màu là:
⦁ Hình 84: Diện tích hình tròn có bán kính 2 cm là S1 = π.22 = 4π (cm2).
Diện tích hình quạt tròn có bán kính 2 cm, số đo cung 72° là:
Vậy diện tích phần được tô màu là:
⦁ Hình 85: Diện tích phần được tô màu chính là diện tích hình vành khuyên được giới hạn bởi hai đường tròn cùng tâm bán kính 24 cm và 6 cm, và bằng:
S = π.(242 – 62) = 540π (cm2).
⦁ Hình 86: Đường tròn nhỏ bên trong có bán kính là 19 cm. Đường tròn to bên ngoài có bán kính là 2.19 = 38 cm.
Diện tích phần được tô màu chính là nửa diện tích hình vành khuyên được giới hạn bởi hai đường tròn cùng tâm có bán kính 38 cm và 19 cm, và bằng:
b) Cách 1: Tính độ dài cung tròn theo công thức
⦁ Hình 83: Số đo cung tròn được tô màu xanh là: 360° – 40° = 320°.
Độ dài cung tròn được tô màu xanh là:
⦁ Hình 84: Độ dài cung tròn được tô màu xanh là:
Cách 2: Tính độ dài cung tròn theo diện tích của cung đó.
Ta có do đó
⦁ Hình 83: Diện tích của hình tròn bán kính 2 cm là π.22 = 4π (cm2).
Diện tích của phần không tô màu là:
Độ dài cung tròn được tô màu xanh là:
⦁ Hình 84: Độ dài cung tròn được tô màu xanh là:
Lời giải:
Diện tích hình vành khuyên bên trong là: S1 = π(182 – 152) = 99π (cm2).
Diện tích hình vành khuyên bên ngoài là S1 = π(242 – 212) = 135π (cm2).
Lời giải:
Tổng diện tích hai nửa hình tròn đường kính 2 cm (bán kính 1 cm) chính là diện tích của một hình tròn bán kính 1 cm, và bằng: S1 = π.12 = π (cm2).
Tổng diện tích hai hình chữ nhật kích thước 2 cm × 8 cm là: S2 = 2.(2.8) = 32 (cm2).
Diện tích một phần tư hình vành khuyên giới hạn bởi hai đường tròn cùng tâm có bán kính lần lượt là 4 cm và 6 cm là:
Diện tích của mặt cắt của khung gỗ đó là:
S = S1 + S2 + S3 = π + 32 + 5π = 6π + 32 (cm2).
a) Diện tích của nêm cong là bao nhiêu centimét vuông (lấy 1 ft = 30,48 cm, 1 in = 2,54 cm và làm tròn kết quả đến hàng đơn vị)?
b) Cần phải biết những kích thước nào của nêm góc để tính được diện tích của nêm đó?
Lời giải:
Đổi 3ft = 91,44 cm; 6 in = 15,24 cm.
a) Bán kính IQ là 91,44 + 15,24 = 106,68 (cm).
Diện tích của nêm cong MNPQ là:
S = π(106,682 – 15,242) = 11148,3648π (cm2) ≈ 35 024 (cm2).
b) Diện tích nêm góc ABCD là:
Xét ∆OAE vuông tại A, ta có: AE = OA.tan
Do đó
Vậy để tính được diện tích của nêm góc ABCD, ta cần biết những kích thước: OB, OA và số đo góc AOE.
Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
§5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
§1. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
§3. Tần số ghép nhóm. Tần số tương đối ghép nhóm
Lý thuyết Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
1. Độ dài cung tròn
Tỉ số giữa chi vi C của mỗi đường tròn với đường kính d của đường tròn đó là một hằng số, kí hiệu là . Số là số vô tỉ, cụ thể:
- Chu vi đường tròn đường kính d là .
- Chu vi đường tròn bán kính R là .
Công thức tính độ dài cung tròn
|
Trong một đường tròn bán kính R, độ dài của cung tròn có số đo là . |
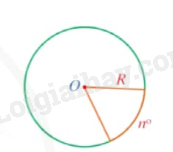
Ví dụ:
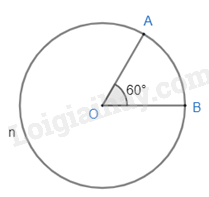
Đường tròn (O; 2cm), .
- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.
Do đó sđ
Độ dài của cung AB là:
Cung lớn AnB có số đo là:
sđ.
Độ dài của cung AnB là:
2. Diện tích hình quạt tròn
Chú ý:
- Hình tròn tâm O bán kính R bao gồm đường tròn (O;R) và tất cả các điểm nằm trong đường tròn đó.
- Diện tích của hình tròn bán kính R là .
Khái niệm hình quạt tròn
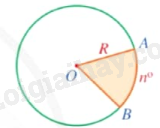
|
Hình quạt tròn (hay còn gọi tắt là hình quạt) là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó. |
Diện tích hình quạt tròn
|
Diện tích hình quạt tròn bán kính R ứng với cung :
|
Nhận xét: Gọi là độ dài của cung tròn có số đo thì diện tích hình quạt tròn bán kính R, cung tròn có số đo là:
.
Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là cm, bán kính là R = 5cm là:
3. Diện tích hình vành khuyên
Khái niệm hình vành khuyên
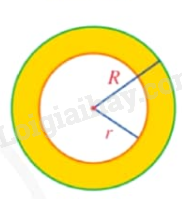
|
Hình giới hạn bởi hai đường tròn cùng tâm được gọi là hình vành khuyên. |
Diện tích hình vành khuyên
|
Hình vành khuyên giới hạn bởi hai đường tròn (O;R) và (O;r) (với R > r) có diện tích là: |
|
. |
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là: