Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 3: Tiếp tuyến của đường tròn chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 3: Tiếp tuyến của đường tròn

Khởi động trang 106 Toán 9 Tập 1: Quan sát máy cắt sắt đang hoạt động (Hình 32), ta thấy các mảnh vụn sắt chuyển động và văng ra theo phương tiếp tuyến với đường tròn mép đĩa cắt.

Tiếp tuyến của đường tròn có tính chất và được nhận biết như thế nào?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

– Tính chất của tiếp tuyến của đường tròn: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.

– Nhận biết tiếp tuyến của đường tròn: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn.

Hoạt động 1 trang 106 Toán 9 Tập 1: Cho đường thẳng a là tiếp tuyến của đường tròn (O; R). Gọi H là hình chiếu của tâm O trên đường thẳng a (Hình 33).

a) So sánh khoảng cách OH từ tâm O đến đường thẳng a và bán kính R.

b) Điểm H có thuộc đường tròn (O; R) hay không?

c) Điểm H có phải là tiếp điểm của đường thẳng a và đường tròn (O; R) hay không?

d) Đường thẳng a có vuông góc với bán kính đi qua tiếp điểm hay không?

Lời giải:

a) Vì đường thẳng a là tiếp tuyến của đường tròn (O; R) nên khoảng cách OH từ tâm O đến đường thẳng a bằng bán kính R.

Vậy OH = R.

b) Vì OH = R nên điểm H có thuộc đường tròn (O; R).

c) Điểm H là điểm chung của đường thẳng a và đường tròn (O; R) nên H là tiếp điểm của đường thẳng a và đường tròn (O; R).

d) Đường thẳng a vuông góc với bán kính OH đi qua tiếp điểm H.

1. Nhận biết tiếp tuyến của đường tròn

Luyện tập 1 trang 107 Toán 9 Tập 1: Cho ba điểm A, B, C thẳng hàng, trong đó B nằm giữa A và C. Đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C. Chứng minh AO² + BC² = BO² + AC².

Lời giải:

Vì đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C nên OC ⊥ AC tại C.

Xét ∆OAC vuông tại C, ta có: AO² = AC² + CO² (định lí Pythagore).

Suy ra CO² = AO² – AC².

Xét ∆OBC vuông tại C, ta có: BO² = BC² + CO² (định lí Pythagore).

Suy ra CO² = BO² – BC².

Do đó AO² – AC² = BO² – BC²

Hay AO² + BC² = BO² + AC².

Hoạt động 2 trang 107 Toán 9 Tập 1: Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O; R) và a ⊥ OH (Hình 35).

a) So sánh khoảng cách từ điểm O đến đường thẳng a và bán kính R.

b) Giả sử N là điểm thuộc đường thẳng a và N khác H. So sánh ON và R. Điểm N có thuộc đường tròn (O; R) hay không?

c) Đường thẳng a có phải là tiếp tuyến của đường tròn (O; R) hay không?

Lời giải:

a) Vì OH ⊥ a tại H nên khoảng cách từ điểm O đến đường thẳng a là OH = R.

b) Ta có ON, OH lần lượt là đường xiên và đường vuông góc kẻ từ O đến đường thẳng a nên ON > OH hay ON > R.

Do đó điểm N nằm ngoài đường tròn (O; R).

c) Ta có a vuông góc với bán kính OH tại điểm H nên a là tiếp tuyến của đường tròn (O; R) tại tiếp điểm H.

Luyện tập 2 trang 107 Toán 9 Tập 1: Cho đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại điểm I. Gọi d là tiếp tuyến của (O; R) tại điểm I. Chứng minh d là tiếp tuyến của (O’; R’).

Lời giải:

Vì đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại điểm I nên ba điểm O, I, O’ thẳng hàng và I nằm giữa O và O’.

Vì đường thẳng d là tiếp tuyến của đường tròn (O; R) tại I nên d ⊥ OI tại I.

Do đó d ⊥ O’I tại I, mà I thuộc đường tròn (O’; R’) nên d là tiếp tuyến của (O’; R’).

Luyện tập 3 trang 108 Toán 9 Tập 1: Cho hai đường tròn (O), (O’) cắt nhau tại hai điểm A, B sao cho đường thẳng OA là tiếp tuyến của đường tròn (O’). Chứng minh đường thẳng O’B là tiếp tuyến của đường tròn (O).

Lời giải:

Vì hai đường tròn (O), (O’) cắt nhau tại hai điểm A, B nên OA = OB và O’A = O’B.

Xét ∆OAO’ và ∆OBO’ có:

OA = OB; O’A = O’B; OO’ là cạnh chung

Do đó ∆OAO’ = ∆OBO’ (c.c.c).

Suy ra $\widehat{OA{O}^{\text{'}}}=\widehat{OB{O}^{\text{'}}}$ (hai góc tương ứng).

Mặt khác, OA là tiếp tuyến của đường tròn (O’) nên OA ⊥ AO’ tại A hay $\widehat{OA{O}^{\text{'}}}=90°.$

Do đó $\widehat{OB{O}^{\text{'}}}=90°,$ hay OB ⊥ BO’ tại B nên O’B là tiếp tuyến của đường tròn (O).

2. Tính chất của hai tiếp tuyến cắt nhau

Hoạt động 3 trang 108 Toán 9 Tập 1: Cho đường tròn (O; R). Các đường thẳng c, d lần lượt tiếp xúc với đường tròn (O; R) tại A, B và cắt nhau tại M (Hình 38).

a) Các tam giác MOA và MOB có bằng nhau hay không?

b) Hai đoạn thẳng MA và MB có bằng nhau hay không?

c) Tia MO có phải là tia phân giác của góc AMB hay không?

d) Tia OM có phải tia phân giác của góc AOB hay không?

Lời giải:

a) Xét ∆MOA (vuông tại A) và ∆MOB (vuông tại B) có:

OA = OB = R (A, B cùng thuộc đường tròn (O; R));

OM là cạnh chung.

Do đó ∆MOA = ∆MOB (cạnh huyền – cạnh góc vuông).

b) Vì ∆MOA = ∆MOB (câu a) nên MA = MB (hai cạnh tương ứng).

c) Vì ∆MOA = ∆MOB (câu a) nên $\widehat{OMA}=\widehat{OMB}$ (hai góc tương ứng)

Do đó MO là phân giác của $\widehat{AMB}.$

d) Vì ∆MOA = ∆MOB (câu a) nên $\widehat{MOA}=\widehat{MOB}$ (hai góc tương ứng)

Do đó OM là phân giác của $\widehat{AOB}.$

Luyện tập 4 trang 109 Toán 9 Tập 1: Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d qua M lần lượt tiếp xúc với (O) tại A, B. Biết $\widehat{AMB}=120°.$ Chứng minh AB = R.

Lời giải:

Vì MA, MB là hai tiếp tuyến của đường tròn (O; R) nên OA = OB = R và OA ⊥ AM tại A, OB ⊥ BM tại B hay $\widehat{OAM}=90°;\widehat{OBM}=90°.$

Xét tứ giác OAMB có: $\widehat{AOB}+\widehat{OAM}+\widehat{OBM}+\widehat{AMB}=360°$ (định lí tổng các góc của một tứ giác).

Suy ra $\widehat{AOB}=360°-\left(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}\right)$

Nên $\widehat{AOB}=360°-\left(90°+90°+120°\right)=60°.$

Xét tam giác OAB có OA = OB = R và $\widehat{AOB}=60°$ nên là tam giác đều.

Do đó AB = OA = OB = R.

Vậy AB = R.

Bài tập

Bài 1 trang 109 Toán 9 Tập 1: Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong Hình 41a, có một sợi dây không dãn vắt qua ròng rọc.

Giả sử ròng rọc được minh họa bởi đường tròn (O), sợi dây vắt qua ròng rọc được minh họa bởi nửa đường tròn MtN và hai tiếp tuyến Ma, Nb của đường tròn (O) (Hình 41b). Chứng minh Ma // Nb.

Lời giải:

Do Ma, Nb là các tiếp tuyến của đường tròn (O) tại M nên Ma ⊥ OM tại M và Nb ⊥ ON tại N.

Mà MtN là nửa đường tròn nên MN là đường kính đi qua tâm O.

Do đó Ma ⊥ MN và Nb ⊥ MN, suy ra Ma // Nb.

Bài 2 trang 109 Toán 9 Tập 1: Cho đường tròn (O) và dây AB. Điểm M nằm ngoài đường tròn (O) thỏa mãn điểm B nằm trong góc MAO và $\widehat{MAB}=\frac{1}{2}\widehat{AOB}.$ Chứng minh đường thẳng MA là tiếp tuyến của đường tròn (O).

Lời giải:

Kẻ OH ⊥ AB tại H và OH cắt BM tại N.

Xét ∆OAB có OA = OB (bán kính đường tròn (O)) nên ∆OAB cân tại A.

∆OAB cân tại A có đường cao OH nên OH đồng thời là đường phân giác của $\widehat{AOB}.$

Suy ra $\widehat{AOH}=\frac{1}{2}\widehat{AOB}.$

Theo bài, $\widehat{MAB}=\frac{1}{2}\widehat{AOB}$ nên $\widehat{AOH}=\widehat{MAB}.$

Xét ∆OAH vuông tại H, ta có: $\widehat{AOH}+\widehat{OAH}=90°$ (tổng hai góc nhọn trong tam giác vuông)

Suy ra $\widehat{MAB}+\widehat{OAH}=90°$ hay $\widehat{OAM}=90°.$

Do đó MA ⊥ OA tại A, mà OA là bán kính của đường tròn (O) nên MA là tiếp tuyến của đường tròn (O).

Bài 3 trang 110 Toán 9 Tập 1: Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d đi qua M lần lượt tiếp xúc với (O) tại A, B. Tia phân giác của góc MAB cắt MO tại I. Chứng minh điểm I cách đều ba đường thẳng MA, MB và AB.

Lời giải:

Gọi H, K và N lần lượt là hình chiếu của I lên MA, MA và AB.

Theo cách vẽ, ta có IH ⊥ MA, IK ⊥ MB, IN ⊥ AB nên $\widehat{IHA}=\widehat{IHM}=\widehat{IKM}=\widehat{ANI}=90°.$

Xét ∆ANI (vuông tại N) và ∆AHI (vuông tại H) có:

AI là cạnh chung; $\widehat{NAI}=\widehat{HAI}$ (do AI là phân giác của $\widehat{MAB}$).

Do đó ∆ANI = ∆AHI (cạnh huyền – góc nhọn).

Suy ra IN = IH (hai cạnh tương ứng). (1)

Vì MA, MB là hai tiếp tuyến của đường tròn (O) cắt nhau tại M với A, B là các tiếp điểm nên MO là tia phân giác của $\widehat{AMB}$ hay MI là tia phân giác của $\widehat{HMK}.$

Xét ∆MHI (vuông tại H) và ∆MKI (vuông tại K) có:

MI là cạnh chung và $\widehat{HMI}=\widehat{KMI}$ (do MI là tia phân giác của $\widehat{HMK}$).

Do đó ∆MHI = ∆MKI (cạnh huyền – góc nhọn).

Suy ra IH = IK (hai cạnh tương ứng). (2)

Từ (1) và (2) suy ra IN = IH = IK.

Vậy điểm I cách đều ba đường thẳng MA, MB và AB.

Bài 4 trang 110 Toán 9 Tập 1: Một người quan sát đặt mắt ở vị trí A có độ cao cách mực nước biển là AB = 5 m. Cắt bề mặt Trái Đất bởi một mặt phẳng đi qua điểm A và tâm Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm O. Tầm quan sát tối đa từ vị trí A là đoạn thẳng AC, trong đó C là tiếp điểm của tiếp tuyến đi qua A với đường tròn (O) (minh họa như Hình 42). Tính độ dài của đoạn thẳng AC (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là OB = OC ≈ 6 400 km.

(Nguồn: Toán 9 – Tập một, NXB Giáo dục Việt Nam, năm 2017)

Lời giải:

Theo bài, ta có: AB = 5 m = 0,005 km.

Khi đó, OA = OB + AB ≈ 6 400 + 0,005 = 6 400,005 (km).

Vì AC là tiếp tuyến của đường tròn (O) nên AC ⊥ OC tại C, hay $\widehat{OCA}=90°.$

Do đó ∆OAC vuông tại C.

Theo định lí Pythagore, ta có:

OA² = OC² + AC²

Suy ra AC² = OA² – OC² ≈ 6 400,005² – 6 400² = 64,000025.

Do đó $AC=\sqrt{64,000025}\approx 8,0\text{(km).}$

Vậy AC ≈ 8,0 km.

Bài 5 trang 110 Toán 9 Tập 1: Cho đường tròn (O; R) đường kính AB và các đường thẳng m, n, p lần lượt tiếp xúc với đường tròn tại A, B, C (Hình 43).

Chứng minh:

a) AD + BE = DE;

b) $\widehat{COD}=\frac{1}{2}\widehat{COA}$ và $\widehat{COE}=\frac{1}{2}\widehat{COB}.$

c) Tam giác ODE vuông.

d) $\frac{OD\cdot OE}{DE}=R.$

Lời giải:

a) Vì DA, DC là hai tiếp tuyến của đường tròn (O) cắt nhau tại D nên DA = DC (tính chất hai tiếp tuyến cắt nhau).

Vì EB, EC là hai tiếp tuyến của đường tròn (O) cắt nhau tại E nên EB = EC (tính chất hai tiếp tuyến cắt nhau).

Do đó DA + EB = DC + EC hay AD + BE = DE.

b) Vì DA, DC là hai tiếp tuyến của đường tròn (O) cắt nhau tại D nên OA là tia phân giác của $\widehat{COA}$ (tính chất hai tiếp tuyến cắt nhau).

Do đó $\widehat{COD}=\frac{1}{2}\widehat{COA}$ (tính chất tia phân giác).

Vì EB, EC là hai tiếp tuyến của đường tròn (O) cắt nhau tại E nên OE tia phân giác của $\widehat{COB}$ (tính chất hai tiếp tuyến cắt nhau).

Do đó $\widehat{COE}=\frac{1}{2}\widehat{COB}$ (tính chất tia phân giác).

c) Ta có: $\widehat{DOE}=\widehat{COD}+\widehat{COE}$

Mà $\widehat{COD}=\frac{1}{2}\widehat{COA}$ và $\widehat{COE}=\frac{1}{2}\widehat{COB}$ (chứng minh ở câu b)

Do đó $\widehat{DOE}=\frac{1}{2}\left(\widehat{COA}+\widehat{COB}\right)=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 180°=90°.$

Vậy tam giác ODE vuông tại O.

d) Vì DE là tiếp tuyến của đường tròn (O) tại C nên OC ⊥ DE tại C.

Xét ∆ODE và ∆CDO có:

$\widehat{DOE}=\widehat{DCO}=90°$ và $\widehat{ODE}$ là góc chung

Do đó ∆ODE ᔕ ∆CDO (g.g)

Suy ra $\frac{OE}{CO}=\frac{DE}{DO}$ (tỉ số các cạnh tương ứng)

Nên CO = $\frac{OD\cdot OE}{DE}$ hay $\frac{OD\cdot OE}{DE}$= R.

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

§2. Vị trí tương đối của đường thẳng và đường tròn

§3. Tiếp tuyến của đường tròn

§4. Góc ở tâm. Góc nội tiếp

§5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên

Bài tập cuối chương 5

§1. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ

Lý thuyết Tiếp tuyến của đường tròn

1. Nhận biết tiếp tuyến của đường tròn

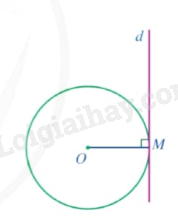
Nhận xét: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.

Dấu hiệu nhận biết tiếp tuyến

2. Tính chất của hai tiếp tuyến cắt nhau

Định lí

Ví dụ: Cho đường tròn (O), B, C $\in$ (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.

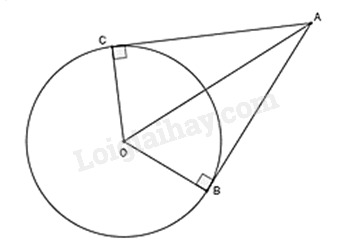
Khi đó:

- AB = AC

- Tia AO là tia phân giác của $\widehat{BAC}$.

- Tia OA là tia phân giác của $\widehat{BOC}$.