Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 3: Giải tam giác và ứng dụng thực tế chi tiết sách Toán 10 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 3: Giải tam giác và ứng dụng thực tế
Video bài giảng Giải tam giác và ứng dụng thực tế - Chân trời sáng tạo
Giải toán lớp 10 trang 74 Tập 1 Chân trời sáng tạo

Phương pháp giải:
Áp dụng định lí cosin:
Lời giải:
Kí hiệu 3 điểm A, B, C như hình dưới.
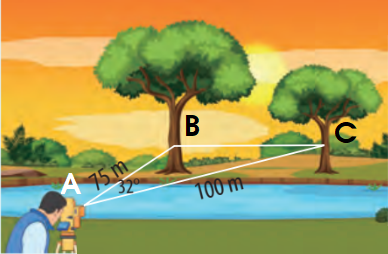
Áp dụng định lí cosin trong tam giác ABC, ta có:
Mà
Vậy khoảng cách giữa hai cây bên bờ sông là 54m.
1. Giải tam giác
Giải toán lớp 10 trang 75 Tập 1 Chân trời sáng tạo
Thực hành trang 75 Toán lớp 10: Giải tam giác ABC trong các trường hợp sau:
a)
b)
Phương pháp giải:
a) Áp dụng định lí sin:
b) Áp dụng hệ quả của định lí cosin:
Lời giải:
a) Ta cần tính góc và hai cạnh
Ta có:
Áp dụng định lí sin, ta có:
b) Ta cần tính số đo ba góc
Áp dụng hệ quả của định lí cosin, ta có:
2. Áp dụng giải tam giác vào thực tế
Giải toán lớp 10 trang 76 Tập 1 Chân trời sáng tạo
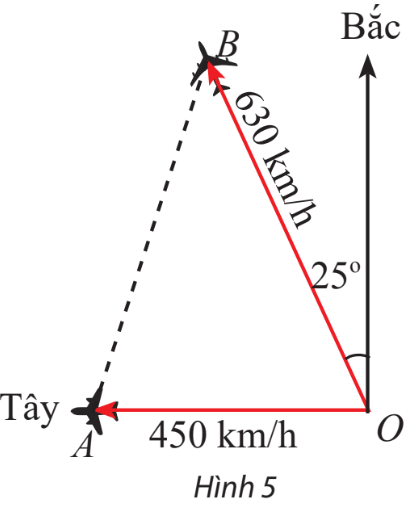
Phương pháp giải:
Bước 1. Tính góc
Bước 2: Áp dụng định lí cosin:
Lời giải:
Ta có:
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là:
Máy bay thứ hai đi được quãng đường (OB) là:
Áp dụng định lí cosin trong tam giác OAB, ta có:
Vậy sau 90 phút, hai máy bay cách nhau khoảng 1009,2 km.
Giải toán lớp 10 trang 77 Tập 1 Chân trời sáng tạo
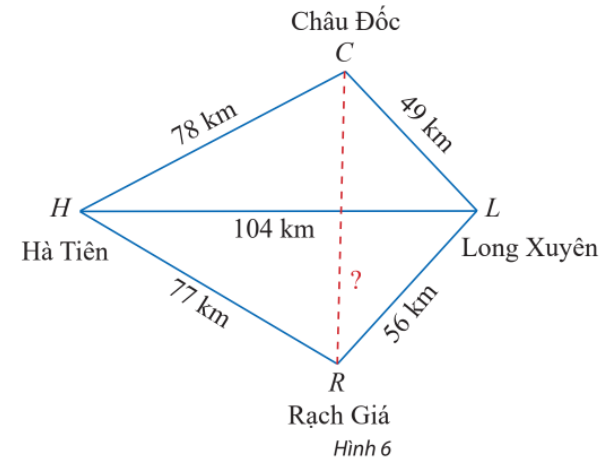
Phương pháp giải:
Bước 1: Áp dụng hệ quả của định lí cosin để tính các góc
Bước 2: Áp dụng định lí cosin
Lời giải:
Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:
Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:
Bước 2: Áp dụng định lí cosin
Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.
Bài tập
Lời giải:
a)
Ta cần tính cạnh BC và hai góc
Áp dụng định lí cosin, ta có:
Áp dụng định lí sin, ta có:
b)
Ta cần tính góc A và hai cạnh AB, AC.
Ta có:
Áp dụng định lí sin, ta có:
c)
Ta cần tính góc A và hai cạnh AB, BC.
Ta có:
Áp dụng định lí sin, ta có:
d)
Ta cần tính số đo ba góc
Áp dụng hệ quả của định lí cosin, ta có:
Phương pháp giải:
Bước 1: Tính cạnh AB: Áp dụng định lí cosin:
Bước 2: Tính chiều dài tăng thêm, bằng
Lời giải:
Áp dụng định lí cosin, ta có:
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
Phương pháp giải:
Kí hiệu các điểm A, B, C như hình dưới.
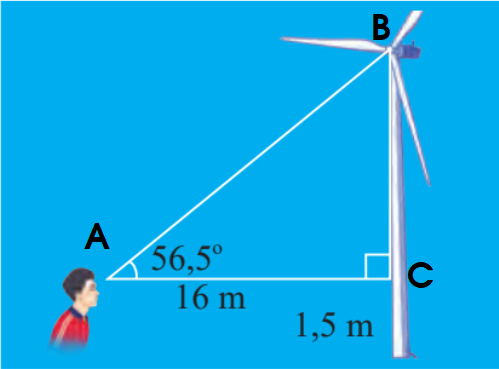
Cách 1:
Tính góc B rồi áp dụng định lí sin để tính BC:
Cách 2:
Lời giải:
Kí hiệu các điểm A, B, C như hình dưới.

Cách 1:
Ta có:
Áp dụng định lí sin, ta có:
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là
Cách 2:
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là
Giải toán lớp 10 trang 78 Tập 1 Chân trời sáng tạo
Phương pháp giải:
Bước 1: Tính AB theo tan góc đối bằng 2 cách (đưa vào hai tam giác ABC và ADB)
Bước 2: Giải phương trình ẩn x, từ đó suy ra AB.
Lời giải:
Tam giác ABC vuông tại B nên ta có:
Tam giác ADB vuông tại B nên ta có:
Vậy chiều cao của ngọn núi là 2,45 km.
Phương pháp giải:
Kí hiệu điểm A là vị trí khinh khí cầu.
Bước 1: Tính góc P, Q, A trong tam giác APQ.
Bước 2: Áp dụng định lí sin, tính QA
Lời giải:
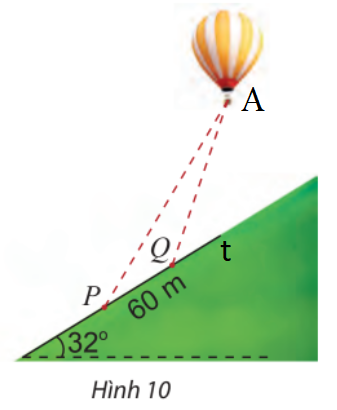
Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình.
Ta có:
Tại P, góc nâng của khinh khí cầu là
Tại Q, góc nâng của khinh khí cầu là
và
Áp dụng định lí sin trong tam giác APQ, ta có:
Vậy khoảng cách từ Q đến khinh khí cầu là 215,56 m.
Phương pháp giải:
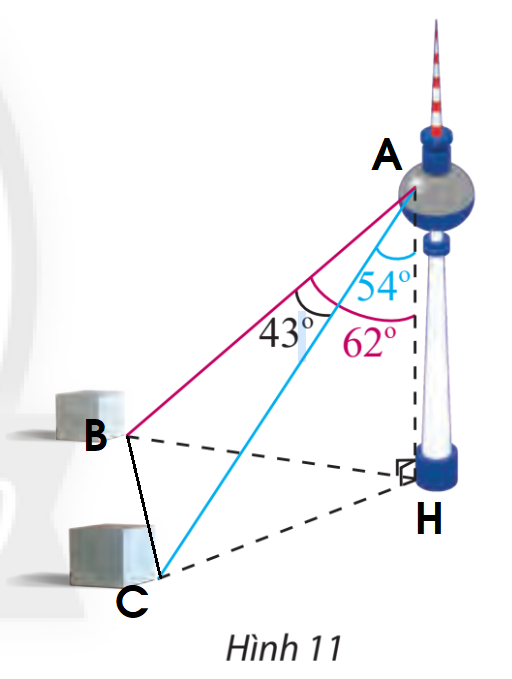
Bước 1: Kí hiệu các điểm A, B, C, H như hình trên.
Bước 2: Tính AB, AC bằng cách gắn vào tam giác ABH và ACH.
Bước 3: Áp dụng định lí cosin cho tam giác ABC:
Lời giải:
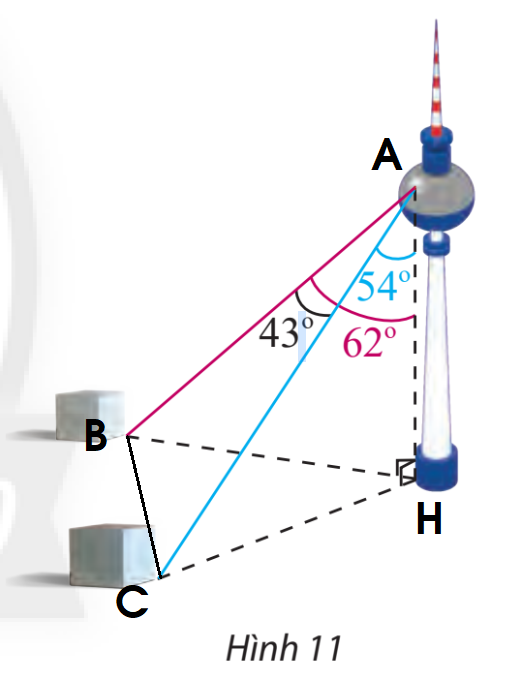
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
Mà
Tương tự, ta có:
Áp dụng định lí cosin cho tam giác ABC, ta có:
Vậy khoảng cách giữa hai cột mốc này là 141,8 m.
Lý thuyết Giải tam giác và ứng dụng thực tế
1. Giải tam giác
Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.
Để giải tam giác, ta thường sử dụng một cách hợp lí các hệ thức lượng như: định lí sin, định lí côsin và các công thức tính diện tích tam giác.
Ví dụ 1. Giải tam giác ABC biết AB = 45, AC = 32 và
Hướng dẫn giải
+) Theo định lí côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA = 452 + 322 – 2.45.32.cos60°
Þ BC2 = 1609.
Þ BC ≈ 40,11.
+) Theo định lí sin ta có:
44° (không thể xảy ra trường hợp do )
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Vậy BC ≈ 40,11; và
2. Áp dụng giải tam giác vào thực tế
Vận dụng giải tam giác giúp ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
Ví dụ 2. Một khung thành bóng đá rộng 5 mét. Một cầu thủ đứng ở vị trí cách cột dọc khung thành 26 mét và cách cột còn lại 23 mét, sút vào khung thành. Tính góc nhìn của cầu thủ tới hai cột khung thành trên.
Hướng dẫn giải
Vị trí cầu thủ C và khung thành AB được mô tả như hình vẽ dưới đây:
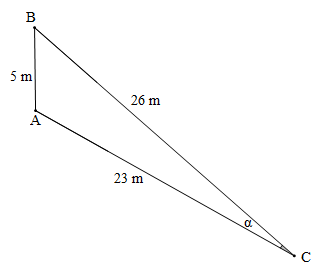
Gọi α là góc nhìn của cầu thủ C tới hai cột khung thành A và B, tức là
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
Suy ra α ≈ 9°23'.
Vậy góc nhìn của cầu thủ tới hai cột khung thành là khoảng 9°23'.
Ví dụ 3. Từ hai vị trí A và B của một toà nhà, người ta quan sát đỉnh C của một ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Tính độ cao của ngọn núi.
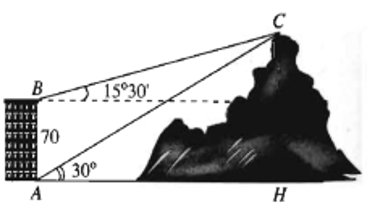
Hướng dẫn giải
Ta có .
Xét tam giác ABC ta có:
(định lí tổng ba góc trong tam giác)
Áp dụng định lí sin ta có:
Þ AC ≈ 269,4 (m)
Tam giác ACH vuông tại H ta có:
Vậy ngọn núi cao khoảng 134,7 m.
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác: