Với giải Bài 5 trang 59 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 3 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài tập cuối chương 3
Bài 5 trang 59 Toán lớp 10: Biết rằng hàm số giảm trên khoảng tăng trên khoảng và có tập giá trị là . Xác định giá trị của m và n.
Phương pháp giải:
Từ tập giá trị suy ra GTNN của hàm số bằng 9.
Lập bảng biến thiên, xác định giá trị nhỏ nhất của hàm số.
Lời giải:
Đỉnh S có tọa độ:
Vì hàm số bậc hai có nên ta có bảng biến thiên sau:

Hàm số đạt giá trị nhỏ nhất bằng
Hàm số giảm trên và tăng trên
Theo giả thiết, ta có:
Hàm số giảm trên khoảng
Tương tự hàm số tăng trên khoảng
Do đó: hay
Lại có: Tập giá trị là Giá trị nhỏ nhất của hàm số bằng 9.
Vậy
Bài tập vận dụng:
Bài 1. Tìm tập xác định của các hàm số sau:
a) ;
b) .
c)
Hướng dẫn giải
a) Biểu thức có nghĩa ⇔ 2x + 1 ≥ 0 ⇔ 2x ≥ ‒ 1 ⇔ x ≥ .
Vậy tập xác định D của hàm số này là D = .
b) Biểu thức có nghĩa ⇔ x + 3 ≠ 0 ⇔ x ≠ ‒3.
Vậy tập xác định D của hàm số này là D = ℝ\ {‒3}.
c) Biểu thức có nghĩa khi và chỉ khi:
Vậy tập xác định của hàm số này là D = [‒2022; +¥) \{0}.
Bài 2. Trong các hàm số sau đây, hàm số nào là đồng biến, nghịch biến? Tại sao?
a) y = f(x) = ‒ 2x + 2.
b) y = f(x) = x2.
Hướng dẫn giải
a) Hàm số y = f(x) = ‒2x + 2 xác định trên ℝ.
Xét hai giá trị x1 = 1 và x2 = 2 đều thuộc ℝ, ta có:
f(x1) = f(1) = ‒2. 1 + 2 = 0.
f(x2) = f(2) = ‒2. 2 + 2 = ‒2.
Ta thấy x1 < x2 và f(x1) > f(x2) nên hàm số y = f(x) = ‒2x + 2 là hàm số nghịch biến trên ℝ.
b) Hàm số y = f(x) = x2 xác định trên ℝ.
Xét hai giá trị x1 = 1 và x2 = 2 đều thuộc ℝ, ta có:
f(x1) = f(1) = 12 = 1.
f(x2) = f(2) = 22 = 4.
Ta thấy x1 < x2 và f(x1) < f(x2) nên hàm số y = f(x) = x2 là hàm số đồng biến trên ℝ.
Bài 3. Tìm tập xác định và vẽ đồ thị hàm số:
y = f(x) = |2x + 3|.
Hướng dẫn giải
Tập xác định của hàm số D = ℝ.
Ta có: y = |2x + 3| =
Ta vẽ đồ thị y = 2x + 3 với (d1)
Ta có bảng sau:
|
x |
0 |
|
|
y = f(x) |
3 |
0 |
Suy ra đồ thị hàm số y = f(x) = 2x + 3 với là phần đồ thị nằm bên trên trục Ox và đi qua các điểm A( ; 0) và B(0; 3).
Ta có đồ thị như sau:
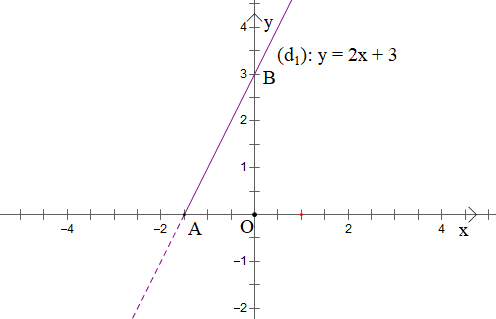
Tương tự ta có đồ thị hàm số y = f(x) = - 2x - 3 với x < - là phần đồ thị nằm bên trên trục Ox và đi qua các điểm C(-2; 1) và D(-3; 3).
Kết hợp 2 đồ thị ta có đồ thị hàm số y = |2x + 3| là phần đồ thị nét liền nằm trên trục Ox.
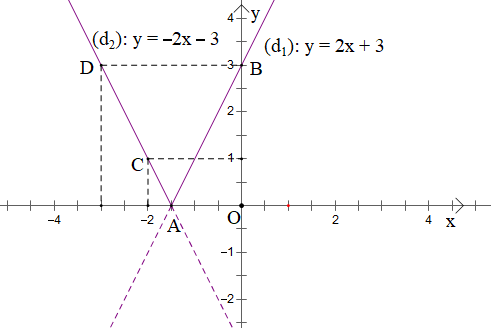
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 59 Toán lớp 10: Tìm tập xác định của các hàm số sau:...
Bài 2 trang 59 Toán lớp 10: Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:...
Bài 3 trang 59 Toán lớp 10: Vẽ đồ thị các hàm số sau:...
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của một góc từ 00 đến 1800
Bài 2: Định lí cosin và định lí sin
Bài 3: Giải tam giác và ứng dụng thực tế