Với giải HĐ 2 trang 6 Toán lớp 7 Kết nối tri thức với cuộc sống chi tiết trong Bài 1: Tập hợp các số hữu tỉ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ
HĐ 2 trang 6 Toán lớp 7: Ta có thể viết
Tương tự, em hãy viết ba phân số bằng nhau và bằng:
a) 2,5; b)
Phương pháp giải:
a) + Viết số thập phân dưới dạng phân số
+ Nhân cả tử và mẫu với một số nguyên khác 0, ta được phân số mới bằng phân số đã cho.
b) + Viết hỗn số dưới dạng phân số
+ Nhân cả tử và mẫu với một số nguyên khác 0, ta được phân số mới bằng phân số đã cho.
Lời giải:
Lý thuyết Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số
• Số hữu tỉ là số viết được dưới dạng phân số với a, b ∈ , b ≠ 0.
Tập hợp các số hữu tỉ được kí hiệu là .
• Cách biểu diễn số hữu tỉ trên trục số:
+ Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.
+ Điểm biểu diễn số hữu tỉ cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).
Ví dụ 1:
+ Các số – 7; 0,3; – 2 là các số hữu tỉ vì chúng viết được dưới dạng phân số: – 7 = ; 0,3 = ; – 2 = .
+ Biểu diễn số hữu tỉ trên trục số ta làm như sau:
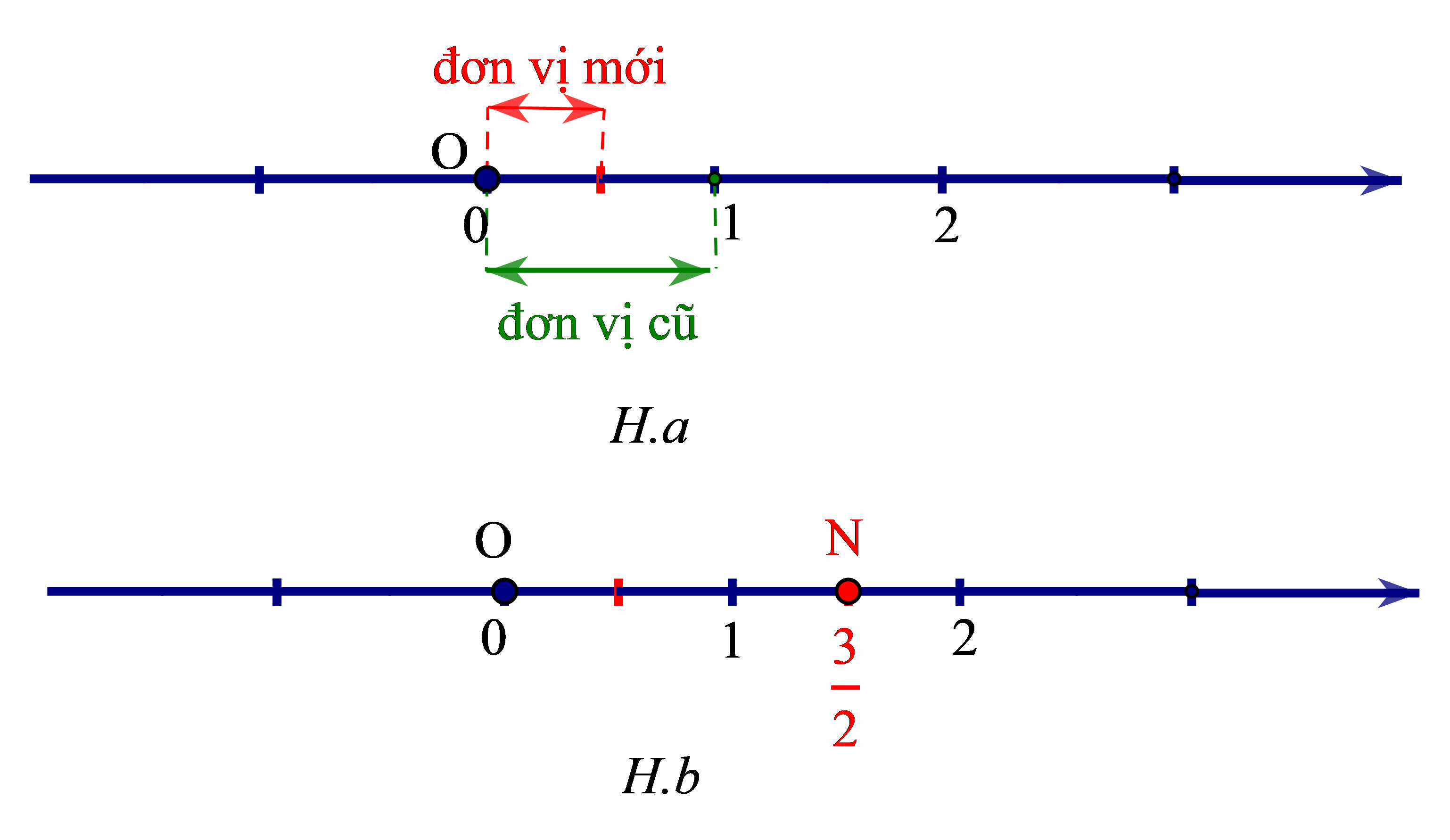
Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).
Số hữu tỉ được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)
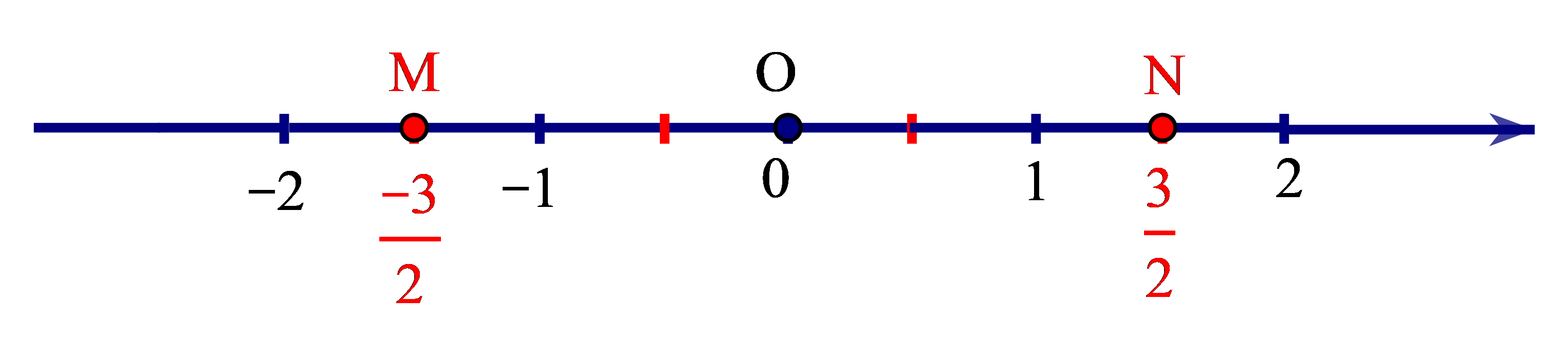
+ Số đối của số hữu tỉ là số hữu tỉ được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.
Chú ý:
• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ – m.
• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.
• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.
Ví dụ 2: Số đối của các số hữu tỉ sau:
Hướng dẫn giải
Số đối của 0 – 9,7 là – (– 9,7) = 9,7;
Số đối của là ;
Số đối của là ;
Số đối của 6 là – 6.
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 2: Cộng, trừ, nhân, chia số hữu tỉ