Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ sách Kết nối tri thức. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài 1: Tập hợp các số hữu tỉ. Mời các bạn đón xem:

Bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ

A. Bài tập Tập hợp các số hữu tỉ

A1. Bài tập tự luận

Bài 1. So sánh:

a) – 1,25 và – 1,125;

b) 0,8 và $\frac{8}{15}$ ;

c) $-\frac{2}{19}$ và $-\frac{10}{19}$ ;

d) $2\frac{2}{3}$ và $\frac{17}{6}$ ;

e) $\frac{1}{2022}$và $\frac{1}{2023}$ ;

f) – 5,6 và $\frac{1}{2}$ ;

g) $\frac{7}{9}$  và 1,5.

Hướng dẫn giải

a) Có 1,25 > 1,125 nên – 1,25 < – 1,125

b) Có  $0,8=\frac{8}{10}=\frac{4}{5}=\frac{12}{15}$ , vì  $\frac{12}{15}>\frac{8}{15}$ . Nên $0,8 >\frac{8}{15}$

c) Có  $\frac{2}{19}<\frac{10}{19}$ nên  $-\frac{2}{19}<-\frac{10}{19}$

d) Có $2\frac{2}{3}=\frac{8}{3}=\frac{16}{6}$ , vì $\frac{16}{6}<\frac{17}{6}$. Nên $2\frac{2}{3}<\frac{17}{6}$

e) $\frac{1}{2022}>\frac{1}{2023}$

f) Có – 5,6 < 0 và  $\frac{1}{2}$> 0. Nên – 5,6 < $\frac{1}{2}$

g) Có $\frac{7}{9}$< 1 và 1,5 > 1. Nên $\frac{7}{9}$< 1,5.

Bài 2. Điền kí hiệu (∈, ∉) thích hợp vào chỗ chấm:

a) 0,15 … $\mathrm{\mathbb{Q}}$ ;

b) $-\frac{5}{0}$  … $\mathrm{\mathbb{Q}}$ ;

c) 1,0 … $\mathrm{\mathbb{Q}}$ ;

d) $\frac{1,2}{8}$  … $\mathrm{\mathbb{Q}}$ .

Hướng dẫn giải

a) Vì 0,15 = $\frac{15}{100}=\frac{3}{20}$  (trong đó 3; 20 ∈ ℤ và 20 ≠ 0) nên 0,15 $\in \mathrm{\mathbb{Q}}$   

b) Ta có: $-\frac{5}{0}$  (trong đó 5; 0 ∈ ℤ và 0 = 0) nên $-\frac{5}{0}\notin \mathrm{\mathbb{Q}}$

c) Vì 1, 0 = $\frac{1}{1}$ (trong đó 1; 1 ∈ ℤ và 1 ≠ 0) nên 1,0 $\in \mathrm{\mathbb{Q}}$

d) Vì $\frac{1,2}{8}=1,2:8=\frac{12}{10}:8=\frac{12}{10}.\frac{1}{8}=\frac{3}{10}$ (trong đó 3; 10 ∈ ℤ và 10 ≠ 0) nên $\frac{1,2}{8}\in \mathrm{\mathbb{Q}}$.

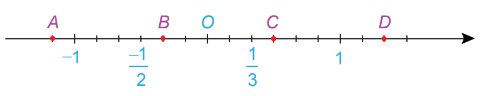
Bài 3. Cho trục số sau:

a) Các điểm A, B, C, D biểu diễn những số hữu tỉ nào?

b) Tìm số đối của các số hữu tỉ trên và biểu diễn chúng trên trục số.

Hướng dẫn giải

a) Ta thấy đoạn thẳng đơn vị cũ (ví dụ đoạn từ 0 đến 1) được chia thành 5 phần bằng nhau nên đoạn đơn vị mới bằng $\frac{1}{5}$  đơn vị cũ. Do đó:

Điểm A nằm trước gốc O và cách gốc O một khoảng bằng 7 đơn vị nên nó biểu diễn số hữu tỉ $-\frac{7}{5}$ .

Tương tự, ta có được:

Điểm B biểu diễn số hữu tỉ $-\frac{2}{5}$ .

Điểm C biểu diễn số hữu tỉ $\frac{4}{5}$ .

Điểm D biểu diễn số hữu tỉ $\frac{9}{5}$ .

b) Số đối của $-\frac{7}{5}$là $-\left(-\frac{7}{5}\right)=\frac{7}{5}$

Số đối của $-\frac{2}{5}$là $-\left(-\frac{2}{5}\right)=\frac{2}{5}$

Số đối của $\frac{4}{5}$là $-\frac{4}{5}$

Số đối của $\frac{9}{5}$là $-\frac{9}{5}$

Biểu diễn trên trục số:

A2. Bài tập trắc nghiệm

Bài 4. Trong các số hữu tỉ: $-1\frac{1}{2}$; -5; 0,75; $\frac{4}{5}$ . Số đối của số hữu tỉ lớn nhất là

A. $\frac{4}{5}$ ;

B. 5;

C. – 0,75;

D. $-\frac{4}{5}$.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: $-1\frac{1}{2}=\frac{-3}{2}$; $-5=\frac{-10}{2}$mà $\frac{-10}{2}<\frac{-3}{2}<0$ nên $-5<-1\frac{1}{2}<0$

$0,75=\frac{3}{4}=\frac{15}{20}$; $\frac{4}{5}=\frac{16}{20}$ mà $\frac{16}{20}>\frac{15}{20}>0$ nên $\frac{4}{5}>0,75>0$

Do đó: $-5<-1\frac{1}{2}<0,75<\frac{4}{5}$

Suy ra số lớn nhất là $\frac{4}{5}$ .

Vậy số đối của $\frac{4}{5}$là $-\frac{4}{5}$ .

Bài 5. Điểm biểu diễn số đối của của số hữu tỉ $\frac{-1}{2}$  là

A. điểm A;

B. điểm B;

C. điểm C;

D. điểm D.

Hướng dẫn giải

Đáp án đúng là: C

Điểm biểu diễn số hữu tỉ đối của $\frac{-1}{2}$  nằm khác phía với $\frac{-1}{2}$  so với điểm O. Như vậy điểm này nằm sau O.

Khoảng cách tử O đến $\frac{-1}{2}$  là 3 đoạn nên khoảng cách từ O đến điểm đó cũng là 3 đoạn.

Vậy điểm biểu diễn số hữu tỉ đối của $\frac{-1}{2}$ là điểm C.

Bài 6. Tập hợp số hữu tỉ được kí hiệu là

A. ℕ;

B. ℤ;

C. ℚ;

D. ℝ.

Hướng dẫn giải

Đáp án đúng là: C

Tập hợp số hữu tỉ được kí hiệu là ℚ.

Câu 7. Dãy các số hữu tỉ được sắp xếp theo chiều tăng dần là

A. $\frac{-1}{9}, \frac{-5}{27}, \frac{7}{25}, \frac{8}{125}$;

B. $\frac{7}{25}, \frac{8}{125}, \frac{-1}{9}, \frac{-5}{27}$;

C. $\frac{-5}{27}, \frac{-1}{9}, \frac{8}{125}, \frac{7}{25}$;

D. $\frac{8}{125}, \frac{7}{25}, \frac{-1}{9}, \frac{-5}{27}$;

Hướng dẫn giải

Câu 8. So sánh đúng là

A. $\frac{2020}{2021}>\frac{2021}{2022}$;

B. $\frac{2020}{2021}=\frac{2021}{2022}$;

C. $\frac{2020}{2021}<\frac{2021}{2022}$;

D. Không so sánh được.

Hướng dẫn giải

Câu 9. Phân số biểu diễn số hữu tỉ -0,625

A. $-\frac{6}{25}$;

B. $-\frac{5}{8}$;

C. $\frac{6}{25}$;

D. $-\frac{625}{100}$;

Hướng dẫn giải

B. Lý thuyết Tập hợp các số hữu tỉ

1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số

• Số hữu tỉ là số viết được dưới dạng phân số $\frac{\mathrm{a}}{\mathrm{b}}$  với a, b ∈ , b ≠ 0.

Tập hợp các số hữu tỉ được kí hiệu là $\mathrm{\mathbb{Q}}$ .

• Cách biểu diễn số hữu tỉ $\frac{\mathrm{a}}{\mathrm{b}}$  trên trục số:

 + Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.

 + Điểm biểu diễn số hữu tỉ $\frac{\mathrm{a}}{\mathrm{b}}$  cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).

Ví dụ 1:

+  Các số – 7; 0,3; – 2$\frac{3}{4}$ là các số hữu tỉ vì chúng viết được dưới dạng phân số: – 7 = $\frac{-7}{1}$ ; 0,3 = $\frac{3}{10}$ ; – 2  = $\frac{-11}{4}$ .

+ Biểu diễn số hữu tỉ  trên trục số ta làm như sau:

Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).

Số hữu tỉ $\frac{3}{2}$  được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)

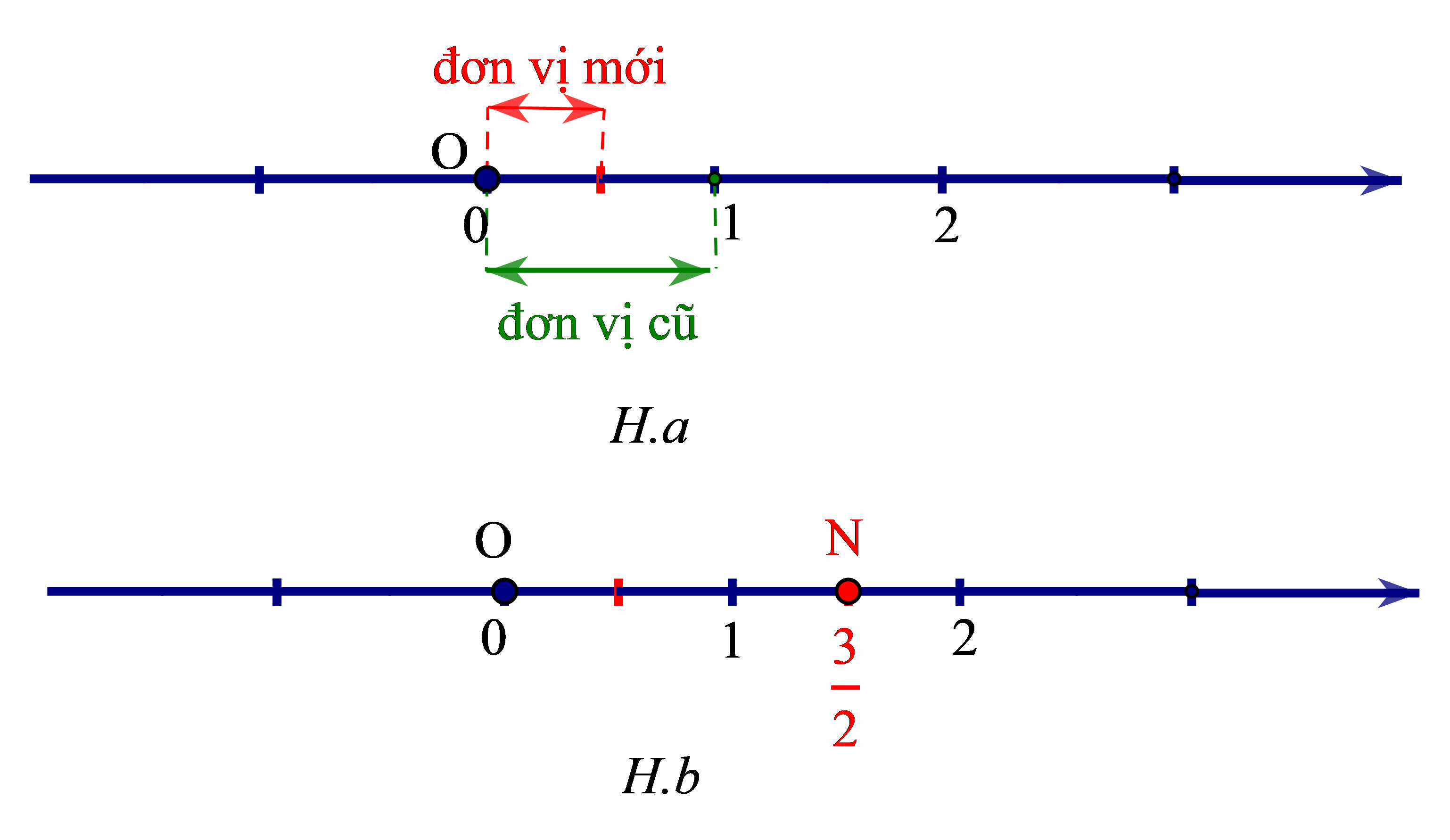
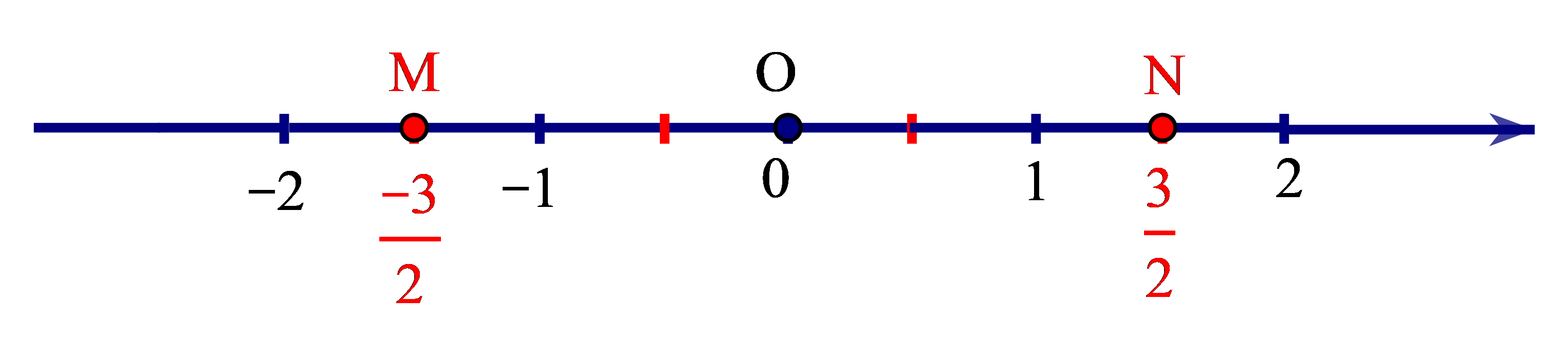
+ Số đối của số hữu tỉ $\frac{3}{2}$  là số hữu tỉ $-\frac{3}{2}$  được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.

Chú ý:

• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ – m.

• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.

• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.

Ví dụ 2: Số đối của các số hữu tỉ sau: $-9,7;3\frac{5}{8};-\frac{1}{2};6.$

Hướng dẫn giải

Số đối của 0 – 9,7 là – (– 9,7) = 9,7;

Số đối của $3\frac{5}{8}$ là $-3\frac{5}{8}$ ;

Số đối của $-\frac{1}{2}$ là $-\left(-\frac{1}{2}\right)=\frac{1}{2}$ ;

Số đối của 6 là  – 6.

2. Thứ tự trong tập hợp các số hữu tỉ

• Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

• Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số, nếu a < b thì điểm a nằm trước điểm b.

Ví dụ:

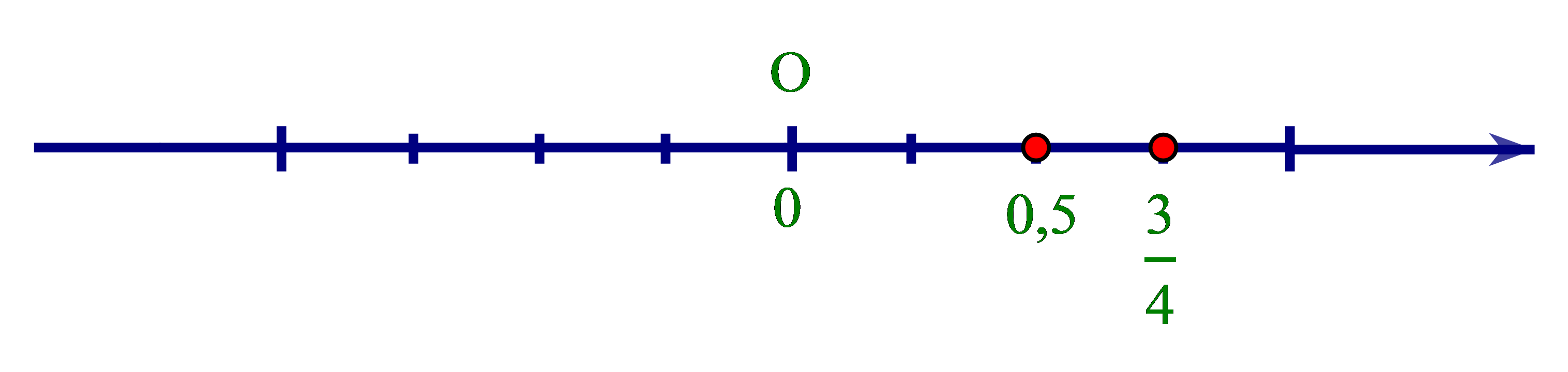
+ So sánh 0,5 và $\frac{3}{4}$  ta làm như sau:

Ta có 0,5 =  $\frac{5}{10}=\frac{1}{2}=\frac{2}{4}$

Vì 2 < 3 nên $\frac{2}{4}$  <  $\frac{3}{4}$hay 0,5 < $\frac{3}{4}$ .

+ 0,5 < $\frac{3}{4}$  nên 0,5 nằm trước $\frac{3}{4}$  trên trục số.

+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ $\frac{5}{6}$  và $\frac{6}{5}$  như sau:

Vì $\frac{5}{6}<\frac{6}{6}=1$ và $1=\frac{5}{5}<\frac{6}{5}$ nên $\frac{5}{6}$ < 1 < $\frac{6}{5}$ .

Vậy $\frac{5}{6}<\frac{6}{5}$ .

Chú ý:

• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.

A. Phương pháp giải

1. Số hữu tỉ

·        Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}$ với $a,b\in Z,b\ne 0$.

·        Tập hợp các số hữu tỉ được kí hiệu là Q.

2. Biểu diễn các số hữu tỉ trên trục số.

·        Mọi số hữu tỉ đều có thể biểu diễn trên trục số.

·        Trên trục số, điểm biểu diễn số hữu tỉ x được gọi là điểm x.

3. So sánh hai số hữu tỉ

·        Để so sánh hai số hữu tỉ, ta viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

·        Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương;

·        Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm;

·        Số hữu tỉ 0, không là số hữu tỉ dương cũng không là số hữu tỉ âm.

·        Số hữu tỉ $\frac{a}{b}$ là số hữu tỉ dương nếu a và b cùng dấu, là số hữu tỉ âm nếu a, b khác dấu, bằng 0 nếu a = 0.

B. Một số ví dụ

Ví dụ 1: Điền các kí hiệu N, Z, Q vào ô trống cho hợp nghĩa (điền tất cả các khả năng có thể):

$-9\in \boxed{}$;                $2020\in \boxed{}$ ;                  $\frac{9}{205}\in \boxed{}$;          $\frac{-21}{10}\in \boxed{}$      

Giải

Tìm cách giải. Khi điền vào ô trống, ta căn cứ vào định nghĩa tập hợp:

·   $N=\left\{0;1;2;3;\mathrm{...}\right\}$     .

·   $Z=\left\{\mathrm{...};-3;-2;-1;0;1;2;3;\mathrm{...}\right\}$    

·  $Q=\left\{x/x=\frac{a}{b};a,b\in Z,b\ne 0\right\}$     

Trình bày lời giải.

·  $-9\in Z;-9\in Q$     

·   $2020\in N;2020\in Z;2020\in Q$    

·   $\frac{9}{205}\in Q$    

·   $-\frac{21}{10}\in Q$    

Nhận xét. Chúng ta lưu ý rằng $N\subset Z\subset Q$, nếu không ý thứ nhất và ý thứ hai của ví dụ dễ bị sót.

Ví dụ 2: Cho số hữu tỉ $x=\frac{a-10}{2020}$. Với giá trị nào của a thì:

a) x là số dương;

b) x là số âm;

c) x không là số dương cũng không là số âm.

Giải

Tìm cách giải. Khi xác định dấu của số hữu tỉ, ta lưu ý $\frac{a}{b}$ là số hữu tỉ dương nếu a và b cùng dấu, là số hữu tỉ âm nếu a, b khác dấu. Chú ý rằng $2020>0$, ta có lời giải sau:

Trình bày lời giải.

a) $x=\frac{a-10}{2020}>0\iff a-10$ và 2020 cùng dấu.

Mà $2020>0$ nên $a-10>0$ suy ra $a>10$. Vậy với $a>10$ thì x là số hữu tỉ dương.

b) $x=\frac{a-10}{2020}>0\iff a-10$ và 2020 khác dấu.

Mà $2020>0$ nên $a-10>0$ suy ra $a<10$. Vậy với $a<10$ thì x là số hữu tỉ âm.

c) x không là số dương cũng không là số âm tức là $x=0$ hay $\frac{a-10}{2020}=0$ suy ra $a=10$.

Vậy với $a=10$ thì x không là số dương cũng không là số âm.

Ví dụ 3. So sánh các số hữu tỉ sau:

a) $x=\frac{-25}{35}$ hay $y=\frac{444}{-777}$;                        

b) $x=-2\frac{1}{5}$ và $y=\frac{110}{-50}$;

c) $x=\frac{17}{20}$ và $y=0,75$.