Với giải sách bài tập Toán 7 Bài 1: Tập hợp các số hữu tỉ sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ

Giải SBT Toán 7 trang 7 Tập 1

Bài 1.1 trang 7 sách bài tập Toán lớp 7 Tập 1:Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;

b) Số hữu tỉ âm nhỏ hơn số tự nhiên;

c) Số 0 là số hữu tỉ dương;

d) Số nguyên âm không phải số hữu tỉ âm;

e) Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm.

Lời giải:

a) Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.

Đây là một khẳng định đúng vì số hữu tỉ âm luôn nhỏ hơn số hữu tỉ dương.

b) Số hữu tỉ âm nhỏ hơn số tự nhiên.

Đây là khẳng định đúng vì số tự nhiên cũng là số hữu tỉ dương mà số hữu tỉ dương luôn lớn hơn số hữu tỉ âm.

c) Số 0 là số hữu tỉ dương.

Đây là khẳng định sai vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

d) Số nguyên âm không phải số hữu tỉ âm.

Đây là khẳng định sai vì số nguyên âm cũng là số hữu tỉ âm.

e) Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm.

Đây là khẳng định sai vì tập hợp ℚ gồm các số hữu tỉ âm, các số hữu tỉ dương và số 0.

Bài 1.2 trang 7 sách bài tập Toán lớp 7 Tập 1: Điền kí hiệu (∈, ∉) thích hợp vào ô vuông:

$-7\boxed{}\mathbb{N};-7\boxed{}\mathbb{Z};-7\boxed{}\mathbb{Q};\frac{-3}{5}\boxed{}\mathbb{Z};\frac{-3}{5}\boxed{}\mathbb{Q}$

Lời giải:

$-7\boxed{\notin }\mathbb{N};-7\boxed{\in }\mathbb{Z};-7\boxed{\in }\mathbb{Q};\frac{-3}{5}\boxed{\notin }\mathbb{Z};\frac{-3}{5}\boxed{\in }\mathbb{Q}$

Bài 1.3 trang 7 sách bài tập Toán lớp 7 Tập 1: Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng:

Lời giải:

Bài 1.4 trang 7 sách bài tập Toán lớp 7 Tập 1: So sánh các số hữu tỉ sau:

a) $-\frac{57}{2021}$ và $\frac{1}{6345}$;

b) $\frac{-19}{35}$ và $\frac{-13}{21}$;

c) $\frac{6}{73}$ và $\frac{9}{82}$.

Lời giải:

a) $-\frac{57}{2021}$ và $\frac{1}{6345}$

Vì $-\frac{57}{2021}$ là số hữu tỉ âm và $\frac{1}{6345}$ là số hữu tỉ dương nên $-\frac{57}{2021}$<$\frac{1}{6345}$.

b) $\frac{-19}{35}$ và $\frac{-13}{21}$

Ta có:

$\frac{-19}{35}=\frac{\left(-19\right).3}{35.3}=\frac{-57}{105}$; $\frac{-13}{21}=\frac{\left(-13\right).5}{21.5}=\frac{-65}{105}$

Vì -57 > -65 nên $\frac{-57}{105}>\frac{-65}{105}$. Do đó $\frac{-19}{35}>\frac{-13}{21}$.

c) $\frac{6}{73}$ và $\frac{9}{82}$

Ta có:

$\frac{6}{73}=\frac{6.82}{73.82}=\frac{492}{5986}$; $\frac{9}{82}=\frac{9.73}{82.73}=\frac{657}{5986}$

Vì 657 > 492 nên $\frac{657}{5986}>\frac{492}{5986}$. Do đó, $\frac{6}{73}<\frac{9}{82}$.

Bài 1.5 trang 7 sách bài tập Toán lớp 7 Tập 1: Máy ảnh thường có nhiều tốc độ màn trập (tức khoảng thời gian mà màn trập mở cửa). Tốc độ màn trập tính bằng giây, thường là $\frac{1}{125};\frac{1}{15};0,125;\frac{1}{60};0,004$ và $\frac{1}{4}$. Hãy sắp xếp các tốc độ này từ nhanh nhất đến chậm nhất.

(Theo imaging.nikon.com)

Lời giải:

Tốc độ trập nhanh nhất nghĩa là thời gian mà màn hình mở cửa là nhỏ nhất.

Ta đi so sánh các số với nhau:

Ta có:

$0,125=\frac{125}{1000}=\frac{1}{8}$; $0,004=\frac{4}{1000}=\frac{1}{250}$.

Ta có: $\frac{1}{125}=\frac{1.48}{125.48}=\frac{48}{6000}$

$\frac{1}{15}=\frac{1.400}{15.400}=\frac{400}{6000}$

$\frac{1}{8}=\frac{1.750}{8.750}=\frac{750}{6000}$

$\frac{1}{60}=\frac{1.100}{60.100}=\frac{100}{6000}$

$\frac{1}{250}=\frac{1.24}{250.24}=\frac{24}{6000}$

$\frac{1}{4}=\frac{1.1500}{4.1500}=\frac{1500}{6000}$

Vì 24 < 48 < 100 < 400 < 750 < 1500 nên

$\frac{24}{6000}<\frac{48}{6000}<\frac{100}{6000}<\frac{400}{6000}<\frac{750}{6000}<\frac{1500}{6000}$

Vậy tốc độ được sắp sếp từ nhanh nhất đến châm nhất là:

0,004; $\frac{1}{125};\frac{1}{60};\frac{1}{15};\frac{1}{8};\frac{1}{4}$.

Giải SBT Toán 7 trang 8 Tập 1

Bài 1.6 trang 8 sách bài tập Toán lớp 7 Tập 1:Các điểm A, B, C, D (H. 1.3) lần lượt biểu diễn các số hữu tỉ nào?

Lời giải:

Ta thấy đoạn thẳng đơn vị từ điểm 0 đến điểm 1 được chia thành 6 phần bằng nhau nên mỗi đơn vị mới bằng $\frac{1}{6}$ đơn vị cũ.

Điểm A nằm về bên trái điểm 0 và cách điểm 0 ba đơn vị mới nên điểm A biểu diễn số hữu tỉ $\frac{-3}{6}$ hay $\frac{-1}{2}$.

Điểm B nằm về bên trái điểm 0 và cách điểm 0 hai đơn vị mới nên điểm B biểu diễn số hữu tỉ $\frac{-2}{6}$ hay $\frac{-1}{3}$.

Điểm C nằm về bên phải điểm 0 và cách điểm 0 hai đơn vị mới nên điểm C biểu diễn số hữu tỉ $\frac{2}{6}$ hay $\frac{1}{3}$.

Điểm D nằm về bên phải điểm 0 và cách điểm 0 bảy đơn vị mới nên điểm D biểu diễn số hữu tỉ $\frac{7}{6}$.

Bài 1.7 trang 8 sách bài tập Toán lớp 7 Tập 1: Hãy biểu diễn hai số hữu tỉ $-\frac{4}{5}$ và $\frac{1}{2}$ trên cùng một trục số.

Lời giải:

Ta có:

$-\frac{4}{5}=-\frac{8}{10}$; $\frac{1}{2}=\frac{5}{10}$.

Ta chia đoạn thẳng đơn vị thành 10 phần bằng nhau. Khi đó, đoạn thẳng đơn vị mới bằng 1 phần mười đoạn thẳng đơn vị cũ.

Điểm biểu diễn phân số $\frac{-8}{10}$ nằm về phía bên trái điểm 0 và cách 0 tám đơn vị mới.

Điểm biểu diễn phân số $\frac{5}{10}$ nằm về phía bên phải điểm 0 và cách 0 năm đơn vị mới.

Bài 1.8 trang 8 sách bài tập Toán lớp 7 Tập 1:Chỉ ra hai phân số có mẫu bằng 7, lớn hơn $\frac{-3}{8}$ và nhỏ hơn $\frac{-1}{8}$.

Lời giải:

Gọi tử số của phân số cần tìm là x ta có:

$\frac{-3}{8}<\frac{x}{7}<\frac{-1}{8}$.

Quy đồng mẫu số ta được:

$\frac{\left(-3\right).7}{8.7}<\frac{x.8}{7.8}<\frac{\left(-1\right).7}{8.7}$ hay $\frac{-21}{56}<\frac{8x}{56}<\frac{-7}{56}$

Mà 8x chia hết cho 8 nên 8x∈ {-16; -8}

Với 8x = -16 thì x = -2.

Với 8x = -8 thì x = -1.

Vậy hai phân số cần tìm là $\frac{-2}{7}$ và $\frac{-1}{7}$

Bài 1.9 trang 8 sách bài tập Toán lớp 7 Tập 1:Bảng sau thống kê thành tích ghi bàn của cầu thủ bóng đá Lionel Messi cho câu lạc bộ FC Barcelona tại giải bóng đá vô địch quốc gia La Liga của Tây Ban Nha trong 5 mùa giải gần đây.

Biết hiệu suất ghi bàn được tính bằng tỉ số giữa số bàn thắng và số trận đấu. Em hãy sắp xếp hiệu suất ghi bàn của Messi từ bé đến lớn và cho biết mùa giải nào thì Messi ghi bàn tốt nhất.

Lời giải:

Hiệu suất ghi bàn của mùa giải 2020 – 2021 là $\frac{30}{35}=\frac{6}{7}$

Hiệu suất ghi bàn của mùa giải 2019 – 2020 là $\frac{25}{33}$

Hiệu suất ghi bàn của mùa giải 2018 – 2019 là $\frac{36}{34}=\frac{18}{17}$

Hiệu suất ghi bàn của mùa giải 2017 – 2018 là $\frac{34}{36}=\frac{17}{18}$

Hiệu suất ghi bàn của mùa giải 2016 – 2017 là $\frac{37}{34}$

Ở đây ta thấy có hai tỉ số có tử số lớn hơn mẫu số và hai tỉ số có mẫu sô lớn hơn tử số nên ta chia thành hai nhóm để so sánh:

Nhóm 1: Tử số lớn hơn mẫu số $\frac{18}{17}$ và $\frac{37}{34}$.

Vì tử số lớn hơn mẫu số nên hai phân số này đều lớn hơn 1.

Ta có: $\frac{18}{17}=\frac{18.2}{17.2}=\frac{36}{34}$.

Vì 36 < 37 nên $\frac{36}{34}<\frac{37}{34}$. Hay $\frac{18}{17}<\frac{37}{34}$.

Nhóm 2: Tử số bé hơn mẫu số $\frac{6}{7}$; $\frac{25}{33}$ và $\frac{17}{18}$

Quy đồng mẫu số:

$\frac{6}{7}=\frac{6.198}{7.198}=\frac{1188}{1386}$

$\frac{25}{33}=\frac{25.42}{33.42}=\frac{1050}{1368}$

$\frac{17}{18}=\frac{17.76}{18.76}=\frac{1292}{1368}$

Vì 1050 < 1188 < 1292 nên

$\frac{1050}{1368}<\frac{1188}{1386}<\frac{1292}{1368}$ hay $\frac{25}{33}<\frac{6}{7}<\frac{17}{18}$

Sắp xếp hiệu xuất ghi bàn từ bé đến lớn là:

$\frac{25}{33}<\frac{6}{7}<\frac{17}{18}<\frac{18}{17}<\frac{37}{34}$.

Mùa giải 2016 – 2017 Messi ghi bàn tốt nhất.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 1: Tập hợp các số hữu tỉ

Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Bài 3: Luỹ thừa với số mũ tự nhiên của một số hữu tỉ

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

SBT Toán 7: Ôn tập chương 1

Lý thuyết Tập hợp các số hữu tỉ

1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số

• Số hữu tỉ là số viết được dưới dạng phân số $\frac{\mathrm{a}}{\mathrm{b}}$  với a, b ∈ , b ≠ 0.

Tập hợp các số hữu tỉ được kí hiệu là $\mathrm{\mathbb{Q}}$ .

• Cách biểu diễn số hữu tỉ $\frac{\mathrm{a}}{\mathrm{b}}$  trên trục số:

 + Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.

 + Điểm biểu diễn số hữu tỉ $\frac{\mathrm{a}}{\mathrm{b}}$  cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).

Ví dụ 1:

+  Các số – 7; 0,3; – 2$\frac{3}{4}$ là các số hữu tỉ vì chúng viết được dưới dạng phân số: – 7 = $\frac{-7}{1}$ ; 0,3 = $\frac{3}{10}$ ; – 2  = $\frac{-11}{4}$ .

+ Biểu diễn số hữu tỉ  trên trục số ta làm như sau:

Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).

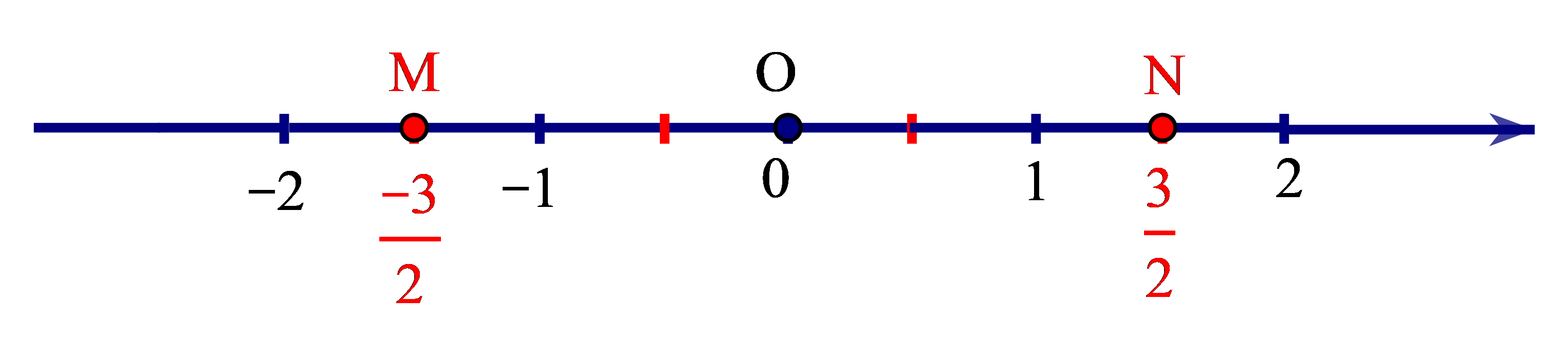
Số hữu tỉ $\frac{3}{2}$  được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)

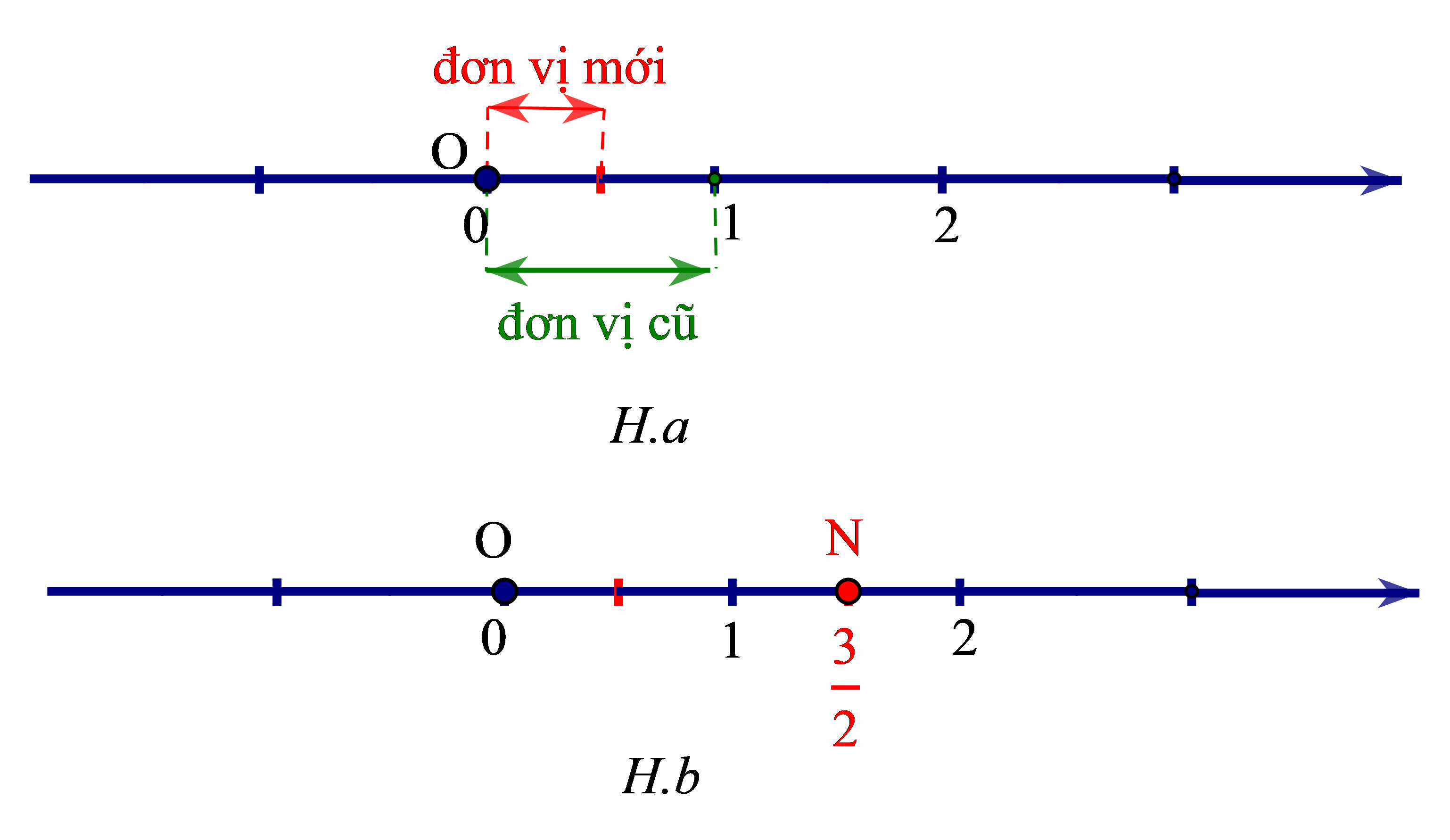
+ Số đối của số hữu tỉ $\frac{3}{2}$  là số hữu tỉ $-\frac{3}{2}$  được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.

Chú ý:

• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ – m.

• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.

• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.

Ví dụ 2: Số đối của các số hữu tỉ sau: $-9,7;3\frac{5}{8};-\frac{1}{2};6.$

Hướng dẫn giải

Số đối của 0 – 9,7 là – (– 9,7) = 9,7;

Số đối của $3\frac{5}{8}$ là $-3\frac{5}{8}$ ;

Số đối của $-\frac{1}{2}$ là $-\left(-\frac{1}{2}\right)=\frac{1}{2}$ ;

Số đối của 6 là  – 6.

2. Thứ tự trong tập hợp các số hữu tỉ

• Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

• Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số, nếu a < b thì điểm a nằm trước điểm b.

Ví dụ:

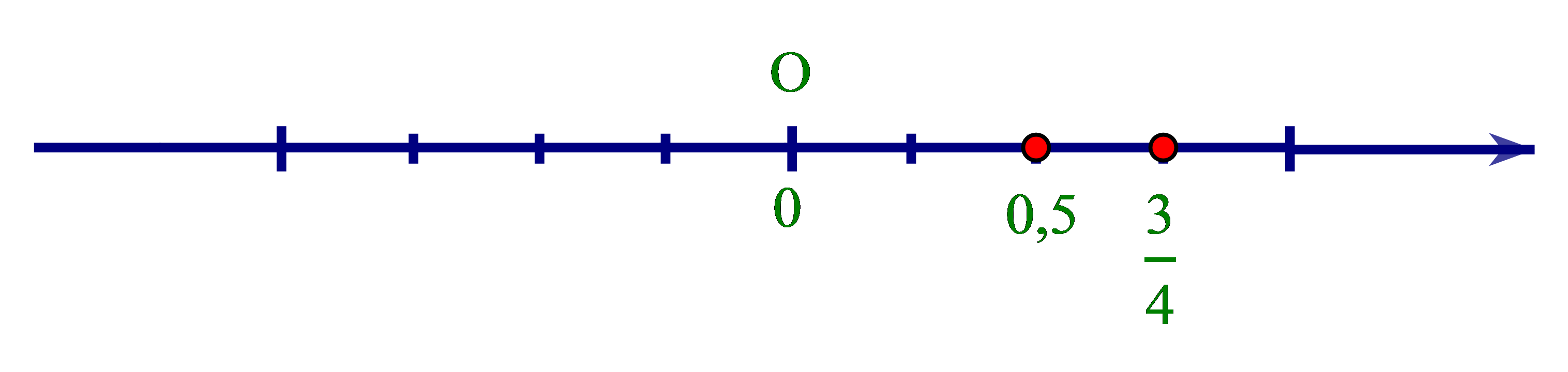
+ So sánh 0,5 và $\frac{3}{4}$  ta làm như sau:

Ta có 0,5 =  $\frac{5}{10}=\frac{1}{2}=\frac{2}{4}$

Vì 2 < 3 nên $\frac{2}{4}$  <  $\frac{3}{4}$hay 0,5 < $\frac{3}{4}$ .

+ 0,5 < $\frac{3}{4}$  nên 0,5 nằm trước $\frac{3}{4}$  trên trục số.

+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ $\frac{5}{6}$  và $\frac{6}{5}$  như sau:

Vì $\frac{5}{6}<\frac{6}{6}=1$ và $1=\frac{5}{5}<\frac{6}{5}$ nên $\frac{5}{6}$ < 1 < $\frac{6}{5}$ .

Vậy $\frac{5}{6}<\frac{6}{5}$ .

Chú ý:

• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.