Tailieumoi.vn giới thiệu Giải bài tập Toán 9 Bài 2: Tỷ số lượng giác của góc nhọn chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Tỷ số lượng giác của góc nhọn 9.
Giải bài tập Toán 9 Bài 2: Tỷ số lượng giác của góc nhọn
Trả lời câu hỏi giữa bài
a)
b)
Phương pháp giải:
a) Sử dụng tính chất tam giác cân
b) Sử dụng tính chất tam giác cân và sử dụng định lý Pytago
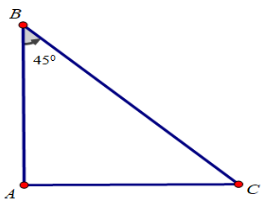
Tam giác ABC vuông tại A có vuông cân tại A
b)
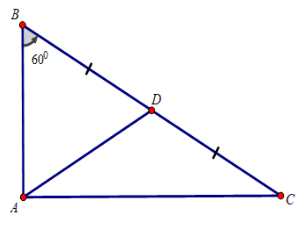
Kẻ trung tuyến AD của tam giác vuông ABC
Tam giác ABD có:
là tam giác đều
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
Lời giải chi tiết
Các tỉ số lượng giác của góc là:
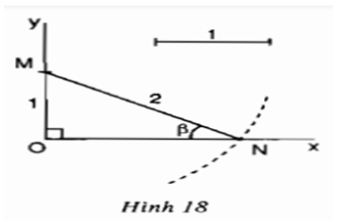
Lời giải:
Cách dựng
- Dựng góc bằng
- Dựng đoạn OM trên trục Oy sao cho OM=1
- Dựng đường tròn tâm M bán kính bằng 2, đường tròn giao với tia Ox tại N
- Khi đó góc MNO là góc cần dựng
Chứng minh:
Tam giác MON vuông tại O có:
Khi đó:
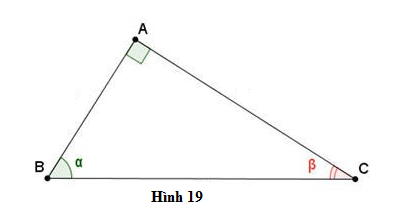
Phương pháp giải:
Sử dụng tổng hai góc nhọn trong tam giác vuông bằng
Sử dụng định nghĩa tỉ số lượng giác của góc nhọn.
+ Các tỉ số lượng giác của góc là
+ Các tỉ số lượng giác của góc là
Suy ra các cặp tỉ số bằng nhau là
Bài tập ( trang 76, 77 SGK Toán 9)
+) Vẽ tam giác thỏa mãn yêu cầu đề bài.
+) Áp dụng công thức tính tỉ số lượng giác của một góc nhọn:
;
Lời giải:
Vẽ tam giác vuông tại với .
Để vẽ được tam giác đề yêu cầu, chúng ta thực hiện các bước như sau:
B1. Vẽ đoạn thẳng với độ dài bất kì.
B2. Từ dựng tia vuông góc với đoạn thẳng
B3. Từ dùng thước đo góc vẽ tia sao cho góc bằng độ.
B4. và cắt nhau tại .
B5. Nối các điểm lại với nhau ta được tam giác cần dựng.
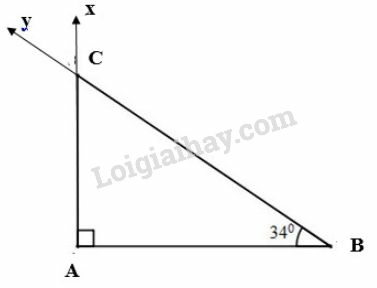
Tỉ số lượng giác của góc là:
Phương pháp giải:
+) Dùng định lí Pytago để tính độ dài cạnh huyền.
+) Dựa vào định nghĩa tỉ số lượng giác để tính các tỉ số lượng giác của góc .
;
+) Dựa vào định lí về tỉ số lượng giác của hai góc phụ nhau: " Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tan góc này bằng cotang góc kia" để từ các tỉ số lượng giác của góc tính tỉ số lượng giác của góc
Lời giải:
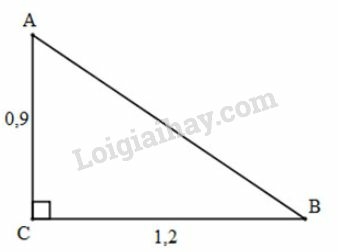
Xét vuông tại , áp dụng định lí Pytago, ta có:
Vì vuông tại nên góc và là hai góc phụ nhau. Do vậy, ta có:
Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tan góc này bằng cotan góc kia!
; ; ; ;
Phương pháp giải:
Nếu và là hai góc phụ nhau (tức thì ta có:
;
;
;
.
Lời giải:
Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:
.
Cách khác:
Vì nên
Vì nên
Vì nên
Vì nên
Vì nên
a)
b)
c)
d)
Phương pháp giải:
+) Dựng một tam giác vuông có hai cạnh là và (trong đó là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền)
+) Vận dụng định nghĩa các tỷ số lượng giác để tìm ra góc .
Lời giải:
a) Ta thực hiện các bước sau:
- Dựng góc vuông . Lấy một đoạn thẳng làm đơn vị.
- Trên tia lấy điểm bất kỳ sao cho: .
- Dùng compa dựng cung tròn tâm , bán kính . Cung tròn này cắt tại điểm .
- Nối với . Góc là góc cần dựng.
Thật vậy, xét vuông tại , theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
.
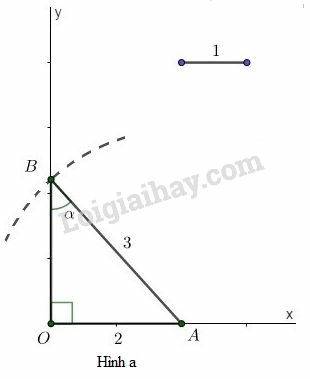
b) Ta có:
- Dựng góc vuông . Lấy một đoạn thẳng làm đơn vị.
- Trên tia lấy điểm bất kỳ sao cho .
- Dùng compa dựng cung tròn tâm bán kính . Cung tròn này cắt tia tại .
- Nối với . Góc là góc cần dựng.
Thật vậy, Xét vuông tại , theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
.
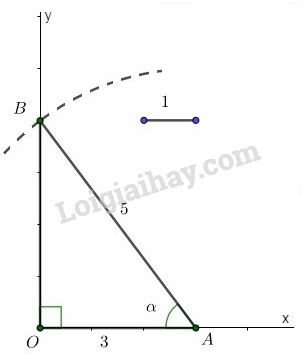
c) - Dựng góc vuông . Lấy một đoạn thẳng làm đơn vị.
- Trên tia lấy điểm sao cho .
Trên tia lấy điểm sao cho .
- Nối với . Góc là góc cần dựng.
Thật vậy, xét vuông tại , theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
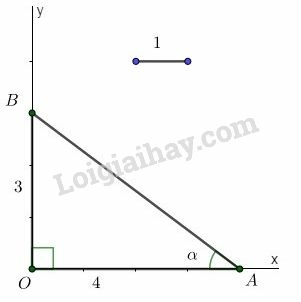
d)- Dựng góc vuông . Lấy một đoạn thẳng làm đơn vị.
- Trên tia lấy điểm sao cho .
Trên tia lấy điểm sao cho .
- Nối với . Góc là góc cần dựng.
Thật vậy, xét vuông tại , theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
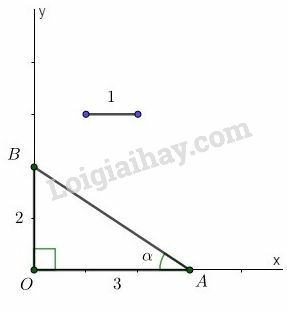
a) ;
b)
Gợi ý: Sử dụng định lý Py-ta-go.
Phương pháp giải:
+) Áp dụng công thức tính tỉ số lượng giác của một góc nhọn:
;
+) Sử dụng định lí Pytago trong tam giác vuông: vuông tại , khi đó:
Lời giải:
Xét vuông tại , có .
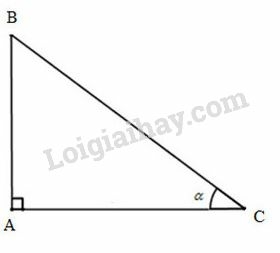
+) , vuông tại , theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
,
, .
* Chứng minh .
(Trong đó VT là vế trái của đẳng thức; VP là vế phải của đẳng thức)
* Chứng minh .
* Chứng minh .
Ta có:
b) vuông tại , áp dụng định lí Pytago, ta được:
(1)
Xét
Như vậy (điều phải chứng minh)
Nhận xét: Ba hệ thức:
; và là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.
Gợi ý: Sử dụng bài tập 14.
Phương pháp giải:
+) Nếu và là hai góc phụ nhau, biết , sử dụng công thức: . Ta tính được .
+) Biết , dùng công thức tính được .
+) Dùng công thức , biết và tính được .
+) Dùng công thức:, biết tính được .
Lời giải:
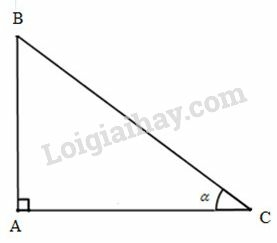
Xét tam giác vuông tại nên góc nhọn. Vì thế:
; ; ; .
Vì hai góc và phụ nhau .
Áp dụng công thức bài 14, ta có:
Lại có:
.
Nhận xét: Nếu biết (hay ) thì ta có thể tính được ba tỷ số lượng giác còn lại.
Phương pháp giải:
Dựa vào định nghĩa tỷ số lượng giác của góc nhọn:
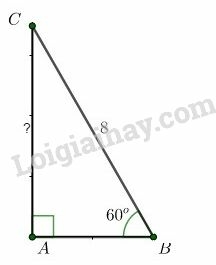
Xét vuông tại có , theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
Vậy cạnh đối diện với góc là .
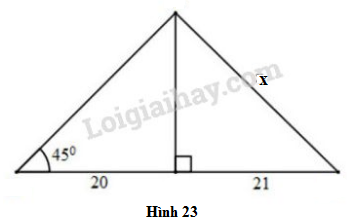
Phương pháp giải:
+) Sử dụng tỷ số lượng giác: .
+) Dùng định lí Pytago trong tam giác vuông biết hai cạnh góc vuông, tính được cạnh huyền.
Lời giải:
Vẽ lại hình và đặt tên các góc như hình sau:
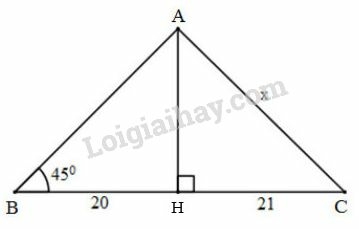
Cách 1:
Xét tam giác vuông tại có , nên:
Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Vậy
Cách 2:
Tam giác ABH vuông tại H có 1 góc bằng nên tam giác ABH vuông cân tại H
, mà BH = 20 nên AH = 20
Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Vậy
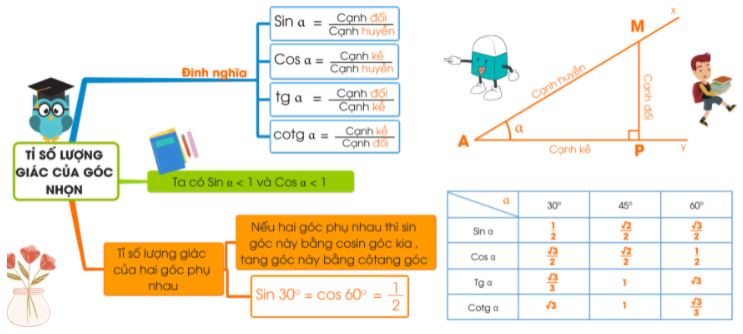
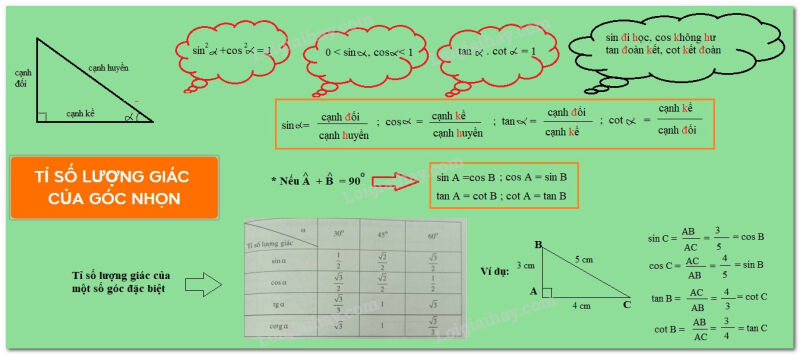
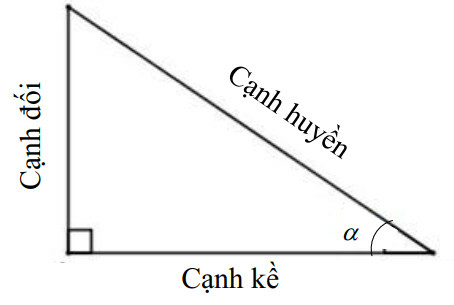
1. Kiến thức cần nhớ
.
Tính chất 1:
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Tức là: Cho hai góc có
Khi đó:
.
Tính chất 2:
+ Nếu hai góc nhọn và có hoặc thì
Tính chất 3:
+ Nếu là một góc nhọn bất kỳ thì
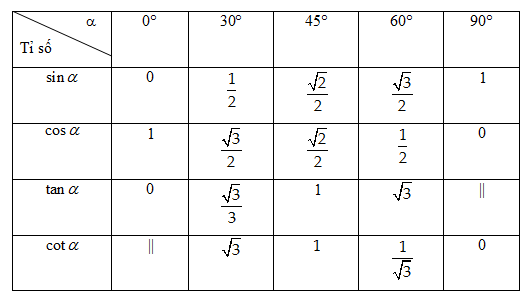
Bảng tỉ số lượng giác các góc đặc biệt
2. Các dạng toán thường gặp
Dạng 1: Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp:
Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Dạng 2: So sánh các tỉ số lượng giác giữa các góc
Phương pháp:
Bước 1 : Đưa các tỉ số lượng giác về cùng loại (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")
Bước 2: Với góc nhọn ta có:
.
Dạng 3: Rút gọn, tính giá trị biểu thức lượng giác
Phương pháp:
Ta thường sử dụng các kiến thức
+ Nếu là một góc nhọn bất kỳ thì
, ,
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.