Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng

Thanh Trà Ngày: 17-10-2022 Lớp 9

1 K

Với giải Bài 14 trang 77 Toán lớp 9 chi tiết trong Bài 2: Tỷ số lượng giác của góc nhọn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 2: Tỷ số lượng giác của góc nhọn

Bài 14 trang 77 SGK Toán 9 Tập 1 :Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn

α

tùy ý, ta có:

a) $\tan α = \frac{\sin α}{\cos α};$ $\cot α = \frac{\cos α}{\sin α};$ $\tan α . \cot α = 1$ ;

b) $\sin^{2} α + \cos^{2} α = 1$

Gợi ý: Sử dụng định lý Py-ta-go.

Phương pháp giải:

+) Áp dụng công thức tính tỉ số lượng giác của một góc nhọn:

$\sin α = \frac{c ạ n h đ ố i}{c ạ n h h u y ề n};$ $\cos α = \frac{c ạ n h k ề}{c ạ n h h u y ề n}$ ;

$\tan α = \frac{c ạ n h đ ố i}{c ạ n h k ề};$ $\cot α = \frac{c ạ n h k ề}{c ạ n h đ ố i} .$

+) Sử dụng định lí Pytago trong tam giác vuông: $Δ A B C$ vuông tại $A$ , khi đó:

$B C^{2} = A B^{2} + A C^{2}$

Lời giải:

Xét $Δ A B C$ vuông tại $A$ , có $\hat{A C B} = α$ .

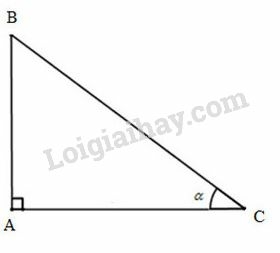
Giải Toán 9 Bài 2: Tỷ số lượng giác của góc nhọn (ảnh 14)

+) $Δ A B C$ , vuông tại $A$ , theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:

$\sin α = \frac{A B}{B C}$ , $\cos α = \frac{A C}{B C}$

$\tan α = \frac{A B}{A C}$ , $\cot α = \frac{A C}{A B}$ .

* Chứng minh $\tan α = \frac{\sin α}{\cos α}$ .

$V P = \frac{\sin α}{\cos α} = \frac{A B}{B C} : \frac{A C}{B C} = \frac{A B}{B C} . \frac{B C}{A C} = \frac{A B}{A C} = \tan α = V T$

(Trong đó VT là vế trái của đẳng thức; VP là vế phải của đẳng thức)

* Chứng minh $\cot α = \frac{\cos α}{\sin α}$ .

$V P = \frac{\cos α}{\sin α} = \frac{A C}{B C} : \frac{A B}{B C} = \frac{A C}{B C} . \frac{B C}{A B} = \frac{A C}{A B} = \cot α = V T$

* Chứng minh $\tan α . \cot α = 1$ .

Ta có: $V T = \tan α . \cot α$

$= \frac{A B}{A C} . \frac{A C}{A B} = 1 = V P$

b) $Δ A B C$ vuông tại $A$ , áp dụng định lí Pytago, ta được:

$B C^{2} = A C^{2} + A B^{2}$ (1)

Xét $\sin^{2} α + \cos^{2} α$

$= {(\frac{A B}{B C})}^{2} + {(\frac{A C}{B C})}^{2} = \frac{A B^{2}}{B C^{2}} + \frac{A C^{2}}{B C^{2}} = \frac{B C^{2}}{B C^{2}} = 1$

Như vậy $\sin^{2} α + \cos^{2} α = 1$ (điều phải chứng minh)

Nhận xét: Ba hệ thức:

$\tan α = \frac{\sin α}{\cos α}$ ; $\cot α = \frac{\cos α}{\sin α}$ và $\sin^{2} α + \cos^{2} α = 1$ là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập