Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9 Bài 2: Tỉ số lượng giác của góc nhọn chọn lọc, có đáp án. Tài liệu có 24 trang gồm 40 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Tỉ số lượng giác của góc nhọn có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.
Giới thiệu về tài liệu:
- Số trang: 24 trang
- Số câu hỏi trắc nghiệm: 40 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Tỉ số lượng giác của góc nhọn có đáp án – Toán lớp 9:
Tỉ số lượng giác của góc nhọn
Câu 1: Cho tam giác MNP vuông tại M. Khi đó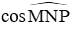 
bằng:
Lời giải:
Đáp án cần chọn là: A
Câu 2: Cho tam giác MNP vuông tại M. Khi đó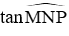 
bằng:
Lời giải:
Đáp án cần chọn là: D
Câu 3: Cho là góc nhọn bất kỳ. Chọn khẳng định đúng.
A. sinα + cosα = 1
B. sin2α + cos2α = 1
C. sin3α + cos3α = 1
D. sinα − cosα = 1
Lời giải:
Cho α là góc nhọn bất kỳ. Khi đó sin2α + cos2α = 1
Đáp án cần chọn là: B
Câu 4: Cho α là góc nhọn bất kỳ. Chọn khẳng định sai:
Lời giải:
Cho α là góc nhọn bất kỳ, khi đó:
Đáp án cần chọn là: D
Câu 5: Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90o. Khẳng định nào sau đây là đúng?
A. tanα = sinβ
B. tanα = cotβ
C. tanα = cosβ
D. tanα = tanβ
Lời giải:
Với hai góc α và β mà α + β = 90o. Ta có:
sinα = cosβ ; cosα = sinβ
tanα = cotβ ; cotα = tanβ
Đáp án cần chọn là: B
Câu 6: Khẳng định nào sau đây là đúng? Cho hai góc phụ nhau thì:
A. sin góc nọ bằng cosin góc kia.
B. sin hai góc bằng nhau
C. tan góc nọ bằng cotan góc kia
D. Cả A và C đều đúng.
Lời giải:
Với hai góc phụ nhau thì sin góc nọ bằng sin góc kia và tan góc nọ bằng cotan góc kia
Đáp án cần chọn là: D
Câu 7: Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác sinB và cosB.
A. sin B = 0,6; cos B = 0,8
B. sin B = 0,8; cos B = 0,6
C. sin B = 0,4; cos B = 0,8
D. sin B = 0,6; cos B = 0,4
Lời giải:
Đáp án cần chọn là: A
Câu 8: Cho tam giác vuông ABC vuông tại C có AC = 1cm, BC = 2cm. Tinh các tỉ số lượng giác sin B, cos B
Lời giải:
Đáp án cần chọn là: B
Câu 9: Cho tam giác ABC vuông tại A có AC = 3; AB = 4. Khi đó cosB bằng:
Lời giải:
Tam giác ABC vuông tại A, áp dụng định lý Py-ta-go ta có:
BC2 = AB2 + AC2 = 42 + 32 = 25 ⇒ BC = 5
Đáp án cần chọn là: D
Câu 10: Cho tam giác ABC vuông tại A có BC = 8cm, AC = 6cm. Tính tỉ số lượng giác tanC. (làm tròn đến chữ số thập phân thứ 2)
A. tan C ≈ 0,87
B. tan C ≈ 0,86
C. tan C ≈ 0,88
D. tan C ≈ 0,89
Lời giải:
Đáp án cần chọn là: C
Câu 11: Cho tam giác ABC vuông tại A có BC = 9cm; AC = 5cm. Tính tỉ số lượng giác tan C (làm tròn đến chữ số thập phân thứ 1)
A. tan C ≈ 0,67
B. tan C ≈ 0,5
C. tan C ≈ 1,4
D. tan C ≈ 1,5
Lời giải:
Đáp án cần chọn là: D
Câu 12: Cho tam giác ABC vuông tại A, đường cao AH có AB = 13cm, BH = 0,5dm. Tính tỉ số lượng giác sinC (làm tròn đến chữ số thập phân thứ 2)
A. sin C ≈ 0,35
B. sin C ≈ 0,37
C. sin C ≈ 0,39
D. sin C ≈ 0,38
Lời giải:
Đổi 0,5dm = 5cm
Xét tam giác ABC vuông tại A, theo hệ thức lượng trong tam giác vuông ta có:
Đáp án cần chọn là: D
Câu 13: Cho tam giác ABC vuông tại A, đường cao AH có AC = 15cm, CH = 6cm. Tính tỉ số lượng giác cos B.
Lời giải:
Xét tam giác AHC vuông tại H, theo định lý Py-ta-go ta có
Mà tam giác ABC vuông tại A nên là hai góc phụ nhau.
Đáp án cần chọn là: B
Câu 14: Cho tam giác ABC vuông tại A, ∠ABC = 60o, cạnh AB = 5cm. Độ dài cạnh AC là:
Lời giải:
Đáp án cần chọn là: C
Câu 15: Cho tam giác ABC vuông tại A, đường cao AH có CH = 4cm, BH = 3cm. Tính tỉ số lượng giác cos C (làm tròn đến chữ số thập phân thứ 2)
A. cos C ≈ 0,76
B. cos C ≈ 0,77
C. cos C ≈ 0,75
D. cos C ≈ 0,78
Lời giải:
Xét tam giác ABC vuông tại A có BC = BH + CH = 7cm
Theo hệ thức lượng trong tam giác vuông ta có:
Đáp án cần chọn là: A
Câu 16: Cho tam giác ABC vuông tại A, đường cao AH có CH = 11cm, BH = 12cm. Tính tỉ số lượng giác cos C (làm tròn đến chữ số thập phân thứ 2)
A. cos C ≈ 0,79
B. cos C ≈ 0,69
C. cos C ≈ 0,96
D. cos C ≈ 0,66
Lời giải:
Xét tam giác ABC vuông tại A có BC = BH + CH = 11 + 12 = 23cm
Theo hệ thức lượng trong tam giác vuông ta có:
Đáp án cần chọn là: B
Câu 17: Cho tam giác ABC vuông tại A. Hãy tính tan C biêt rằng cot B = 2
Lời giải:
Vì tam giác ABC vuông tại A nên:
Đáp án cần chọn là: C
Câu 18: Cho tam giác ABC vuông tại A. Hãy tính tan C biết rằng tan B = 4
Lời giải:
Đáp án cần chọn là: A
Câu 19: Cho tam giác ABC vuông tại A có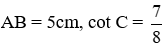 
. Tính độ dài các đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ 2)
A. AC ≈ 4,39 (cm); BC ≈ 6,66 (cm)
B. AC ≈ 4,38 (cm); BC ≈ 6,65 (cm)
C. AC ≈ 4,38 (cm); BC ≈ 6,64 (cm)
D. AC ≈ 4,37 (cm); BC ≈ 6,67 (cm)
Lời giải:
Theo định lý Pytago ta có BC2 = AB2 + AC2 = 52 + 4,382 ⇒ BC ≈ 6,65
Vậy AC ≈ 4,38 (cm); BC ≈ 6,65 (cm)
Đáp án cần chọn là: B
Câu 20: Cho tam giác ABC vuông tại A có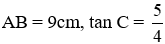 
. Tính độ dài cac đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ hai)
A. AC = 11,53; BC = 7,2
B. AC = 7; BC ≈ 11,53
C. AC = 5,2; BC ≈ 11
D. AC = 7,2; BC ≈ 11,53
Lời giải:
Đáp án cần chọn là: D
Câu 21: Cho α là góc nhọn bất kỳ. Khi đó C = sin6α + cos6α + 3sin2αcos2α bằng:
A. C = 1 − 3sin2α. cos2α
B. C = 1
C. C = sin2α. cos2α
D. C = 3sin2α. cos2α − 1
Lời giải:
Ta có:
sin6α + cos6α + 3sin2αcos2α = sin6α + cos6α + 3sin2αcos2α .1
= sin6α + cos6α + 3sin2αcos2α . (sin2α + cos2α) (vì sin2α + cos2α = 1)
= (sin2α)3 + 3(sin2α)2cos2α + 3 sin2α .( cos2α)2 + (cos2α)3
= (sin2α + cos2α)3 = 1 (vì sin2α + cos2α = 1)
Đáp án cần chọn là: B
Câu 22: Cho α là góc nhọn bất kỳ. Rút gọn P = (1 – sin2α) . cot2 + 1 – cot2 ta được:
A. P = sin2α
B. P = cos2α
C. P = tan2
D. P = 2 sin2
Lời giải:
Đáp án cần chọn là: A
Câu 23: Cho α là góc nhọn bất kỳ. Cho P = (1 – sin2α) . tan2 + (1 – cos2α)cot2α, chọn kết luận đúng.
A. P > 1
B. P < 1
C. P = 1
D. P = 2sin2α
Lời giải:
Đáp án cần chọn là: C
Câu 24: Cho α là góc nhọn bất kỳ. Biểu thức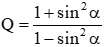 
bằng:
A. Q = 1 + tan2α
B. Q = 1 + 2tan2α
C. Q = 1 − 2tan2α
D. Q = 2tan2α
Lời giải:
Đáp án cần chọn là: B
Câu 25: Cho α là góc nhọn bất kỳ. Biểu thức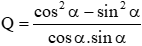 
bằng:
A. Q = cotα − tanα
B. Q = cotα + tanα
C. Q = tanα − cotα
D. Q = 2tanα
Lời giải:
Đáp án cần chọn là: A
Câu 26: Cho tanα = 2. Tính giá trị của biểu thức 
Lời giải:
Đáp án cần chọn là: D
Câu 27: Cho tanα = 4. Tính giá trị của biểu thức 
Lời giải:
Vì tanα = 2 nên cosα ≠ 0, chia cả tử và mẫu của P cho cosα ta được:
Đáp án cần chọn là: A
Câu 28: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD : HA = 1 : 2. Khi đó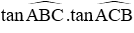 
bằng?
A. 2
B. 3
C. 1
D. 4
Lời giải:
Đáp án cần chọn là: B
Câu 29: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD : HA = 3 : 2. Khi đó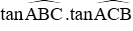 
bằng?
Lời giải:
Đáp án cần chọn là: D
Câu 30: Cho α là góc nhọn. Tính cotα biết 
Lời giải:
Đáp án cần chọn là: A
Câu 31: Tính các giá trị lượng giác còn lại của góc α biết sinα = 
Lời giải:
Đáp án cần chọn là: B
Câu 32: Tính giá trị biểu thức B = tan 1o. tan 2o. tan 3o……. tan 88o. tan 89o.
A. B = 44
B. B = 1
C. B = 45
D. B = 2
Lời giải:
Ta có tan 89o = cot 1o; tan 88o = cot 2o; …; tan 46o = cot 44o và tanα.cotα = 1
Nên B = (tan 1o. tan 89o).(tan 2o.tan 88o) … (tan 46o.tan 44o). tan 45o
= (tan 1o. cot 1o).( tan 2o. cot 2o) . (tan 3o. cot 3o) … (tan 44o. cot 44o). tan 45o
= 1.1.1….1.1 = 1
Vậy B = 1
Đáp án cần chọn là: B
Câu 33: Tính giá trị biểu thức B = tan 10o. tan 20o. tan 30o……. tan 80o.
A. B = 44
B. B = 1
C. B = 45
D. B = 2
Lời giải:
Ta có tan 80 = cot 10o; tan 70o = cot 20o; tan 50o = cot 40o; tan 60o = cot 30o và
tanα.cotα = 1
Nên B = tan 10o. tan 20o. tan 30o. tan 40o. tan 50o. tan 60o. tan 70o. tan 80o
= tan 10o. tan 20o. tan 30o. tan 40o. cot 40o. cot 30o. cot 20o. cot 10o
= (tan 10o. cot 10o) . (tan 20o. cot 20o) . (tan 30o. cot 30o) . (tan 40o. cot 40o)
= 1.1.1.1 = 1
Vậy B = 1
Đáp án cần chọn là: B
Câu 34: Chọn kết luận đúng về giá trị biểu thức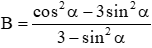 
biết tanα = 3
A. B > 0
B. B < 0
C. 0 < B < 1
D. B = 1
Lời giải:
Vì tanα ≠ 0 cosα ≠ 0. Chia cả tử và mẫu của B cho cos2α ta được:
Đáp án cần chọn là: B
Câu 35: Cho tam giác ABC cân tại A có AB = AC = 13cm; BC = 10cm. Tính sin A
Lời giải:
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
⇒ E là trung điểm BC ⇒ EB = EC = 5
Xét ΔABE vuông tại E có:
Đáp án cần chọn là: A
Câu 36: Tính diện tích hình bình hành ABCD biết AD = 12cm; DC = 15cm; ∠ADC = 70o
A. 139,3cm2
B. 129,6cm2
C. 116,5cm2
D. 115,8cm2
Lời giải:
Xét ADE vuông tại E có:
Đáp án cần chọn là: A
Câu 37: Tính số đo góc nhọn α biết 10sin2α + 6 cos2α = 8
A. α = 30o
B. α = 45o
C. α = 60o
D. α = 120o
Lời giải:
Đáp án cần chọn là: B
Câu 38: Tính giá trị của các biểu thức sau:
A = sin215o + sin225o + sin235o + sin245o + sin255o + sin265o + sin275o
Lời giải:
A = sin215o + sin225o + sin235o + sin245o + sin255o + sin265o + sin275o
Ta có:
A = sin215o + sin225o + sin235o + sin245o + sin255o + sin265o + sin275o
= sin215o + sin225o + sin235o + sin245o + cos235o + cos225o + cos215o
= (sin215o + cos215o) + (sin225o + cos225o) + (sin235o + cos235o) + sin245o
Đáp án cần chọn là: B
Câu 39: Cho hai tam giác vuông OAB và OCD như hình vẽ. Biết OB = OD = a, AB = OD = b. Tính cos ∠AOC theo a và b
Lời giải:
Đáp án cần chọn là: A
Câu 40: Biết 0o < α < 90o. Giá trị của biểu thức:
[sinα + 3cos(90o − α)] : [sinα − 2cos(90o − α)] bằng:
Lời giải:
Đáp án cần chọn là: A
Bài giảng Toán 9 Bài 2: Tỉ số lượng giác của góc nhọn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
