Bài 4.15 trang 59 Toán 10 tập 1 | Kết nối tri thức Giải Toán lớp 10

Bài 4.15 trang 59 Toán 10 tập 1 | Kết nối tri thức Giải Toán lớp 10

Thảo Ngày: 28-03-2023 Lớp 10

6.9 K

Với giải Bài 4.15 trang 59 Toán lớp 10 Kết nối tri thức với cuộc sống trong Bài 9: Tích của một vecto với một số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 9: Tích của một vecto với một số

Bài 4.15 trang 59 Toán lớp 10: Chất điểm A chịu tác động của ba lực $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ như hình 4.30 và ở trạng thái cân bằng (tức là $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{0}$ ). Tính độ lớn của các lực $\vec{F_{2}}, \vec{F_{3}}$ biết $\vec{F_{1}}$ có độ lớn là 20N.

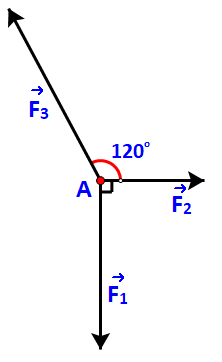
Phương pháp giải:

Bước 1: Xác định vecto $\vec{u} = \vec{F_{1}} + \vec{F_{2}}$ . Từ trạng thái của chất điểm suy ra mối liên hệ (phương, chiều, độ lớn) giữa $\vec{u}$ và $\vec{F_{3}}$ .

Bước 2: Tính độ lớn của $\vec{F_{2}}, \vec{F_{3}}$ .

Lời giải:

Bước 1: Đặt $\vec{u} = \vec{F_{1}} + \vec{F_{2}}$ . Ta xác định các điểm như hình dưới.

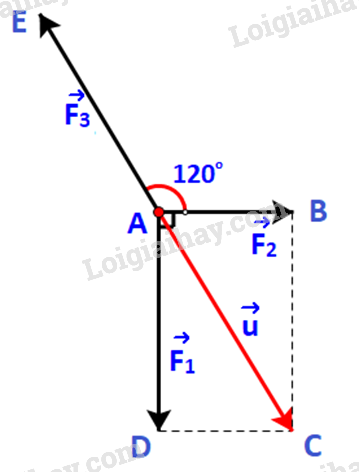
Bài 4.14 trang 58 Toán lớp 10 Tập 1 | Kết nối tri thức (ảnh 2)

Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto $\vec{u}$ chính là vecto $\vec{A C}$

Vì chất điểm A ở trang thái cân bằng nên $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{0}$ hay $\vec{u} + \vec{F_{3}} = \vec{0}$

$\Leftrightarrow \vec{u}$ và $\vec{F_{3}}$ là hai vecto đối nhau.

$\Leftrightarrow A$ là trung điểm của EC.

Bước 2:

Ta có: $| \vec{F_{1}} | = A D = 20, | \vec{F_{2}} | = A B, | \vec{F_{3}} | = A C .$

Do A, C, E thẳng hàng nên $\hat{C A B} = 180^{o} - \hat{E A B} = 60^{o}$

$\begin{array}{l} \Rightarrow \hat{C A D} = 90^{o} - 60^{o} = 30^{o} \\ \Rightarrow {\begin{cases} A C = \frac{A D}{\cos 30^{o}} = \frac{40 \sqrt{3}}{3}; \\ A B = D C = A C . \sin 30^{o} = \frac{20 \sqrt{3}}{3} . \end{cases} \end{array}$

Vậy $| \vec{F_{2}} | = \frac{20 \sqrt{3}}{3}, | \vec{F_{3}} | = \frac{40 \sqrt{3}}{3} .$

Xem thêm các bài giải Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

HĐ1 trang 55 Toán lớp 10: Cho vecto $\vec{A B} = \vec{a}$ . Hãy xác định điểm C sao cho $\vec{B C} = \vec{a}$ ...

Câu hỏi trang 55 Toán lớp 10: $1 \vec{a}$ và $\vec{a}$ có bằng nhau hay không?...

HĐ2 trang 56 Toán lớp 10: Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số $0; 1; \sqrt{2}; - \sqrt{2}$ . Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto $\vec{O M}, \vec{O N}$ với vecto $\vec{a} = \vec{O A}$ . Viết đẳng thức thể hiện mối quan hệ giữa hai vecto $\vec{O M}$ và $\vec{O A}$ ...

Câu hỏi trang 56 Toán lớp 10: $- \vec{a}$ và $- 1 \vec{a}$ có mối quan hệ gì?...

Luyện tập 1 trang 56 Toán lớp 10: Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?...

HĐ3 trang 57 Toán lớp 10: Với $\vec{u} \neq \vec{0}$ và hai số thực k, t, những khẳng định nào sau đây là đúng?...

HĐ4 trang 57 Toán lớp 10: Hãy chỉ ra trên Hình 4.26 hai vecto $3 (\vec{u} + \vec{v})$ và $3 \vec{u} + 3 \vec{v}$ . Từ đó, nêu mối quan hệ giữa $3 (\vec{u} + \vec{v})$ và $3 \vec{u} + 3 \vec{v}$ ...

Luyện tập 2 trang 57 Toán lớp 10: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có

$\vec{O B} + \vec{O A} + \vec{O C} = 3 \vec{O G}$ ...

Luyện tập 3 trang 57 Toán lớp 10: Trong hình 4.27, hãy biểu thị mỗi vecto $\vec{u}, \vec{v}$ theo hai vecto $\vec{a}, \vec{b}$ , tức là tìm các số $x, y, z, t$ để $\vec{u} = x \vec{a} + y \vec{b}, \vec{v} = t \vec{a} + z \vec{b} .$ ..

Bài 4.11 trang 58 Toán lớp 10: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị $\vec{A M}$ theo hai vecto $\vec{A B}$ và $\vec{A D}$ ...

Bài 4.12 trang 58 Toán lớp 10: Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh $\vec{B C} + \vec{A D} = 2 \vec{M N} = \vec{A C} + \vec{B D} .$ ..

Bài 4.13 trang 58 Toán lớp 10: Cho hai điểm phân biệt A và B...

Bài 4.14 trang 58 Toán lớp 10: Cho tam giác ABC...

Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto

Bài tập cuối chương 4

Từ khóa :

Giải bài tập toán 10 Tích của một vecto với một số

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Cho tập hợp A = [0; 6]; B = (a - 2; a + 3]. Có bao nhiêu giá trị nguyên của a để A giao B khác ∅

Cho tập hợp A = [0; 6]; B = (a - 2; a + 3]. Có bao nhiêu giá trị nguyên của a để A giao B khác ∅ Nguyễn Mạnh Tài

11

Toán Tổng hợp kiến thức

Cho tanα + cotα = m. Tìm m để tan^2α + cot^2α = 7

Cho tanα + cotα = m. Tìm m để tan^2α + cot^2α = 7 Nguyễn Mạnh Tài

11

Toán Tổng hợp kiến thức

Cho tan x + cot x = 4. Tính sin x, cos x, tan x, cot x

Cho tan x + cot x = 4. Tính sin x, cos x, tan x, cot x Nguyễn Mạnh Tài

10

Toán Tổng hợp kiến thức

Cho tanα = 2. Tính tan(α-pi/4)

Cho tanα = 2. Tính tan(α-pi/4) Nguyễn Mạnh Tài

10

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack57. All Rights Reserved.