Với giải HĐ1 trang 55 Toán lớp 10 Kết nối tri thức với cuộc sống trong Bài 9: Tích của một vecto với một số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 9: Tích của một vecto với một số
HĐ1 trang 55 Toán lớp 10: Cho vecto . Hãy xác định điểm C sao cho
a) Tìm mối quan hệ giữa và
b) Vecto có mối quan hệ như thế nào về hướng và độ dài đối với vecto
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải:
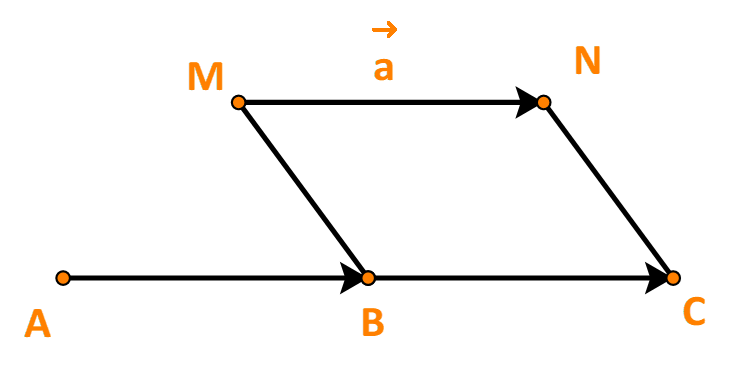
Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto .
Từ B, M, N ta dựng hình bình hành BMNC.
Khi đó: hay .
a) Vì nên A, B, C thẳng hàng và B là trung điểm của AC.
Vậy và cùng hướng,
b) Ta có: và cùng hướng,
Mà nên: và cùng hướng, .
Lý thuyết Tích của một vectơ với một số
• Tích của một vectơ với một số thực k > 0 là một vectơ, kí hiệu là k , cùng hướng với vectơ và có độ dài bằng k .
Ví dụ: Cho hình vẽ sau:
– Vectơ cùng hướng với vectơ và =
– Vectơ cùng hướng với vectơ và = .
• Tích của một vectơ với một số thực k < 0 là một vectơ, kí hiệu là k , ngược hướng với vectơ và có độ dài bằng (–k) ||.
Ví dụ: Cho hình sau:
– Vectơ –2 ngược hướng với vectơ và =
– Vectơ ngược hướng với vectơ và = .
Chú ý: Ta quy ước k = nếu = hoặc k = 0.
Nhận xét: Vectơ k có độ dài bằng |k||| và cùng hướng với nếu k ≥ 0, ngược hướng với nếu ≠ và k < 0.
Chú ý: Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với một số (hay phép nhân một số với vectơ).
Xem thêm các bài giải Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Câu hỏi trang 55 Toán lớp 10: và có bằng nhau hay không?...
Câu hỏi trang 56 Toán lớp 10: và có mối quan hệ gì?...
HĐ3 trang 57 Toán lớp 10: Với và hai số thực k, t, những khẳng định nào sau đây là đúng?...
Bài 4.13 trang 58 Toán lớp 10: Cho hai điểm phân biệt A và B...
Bài 4.14 trang 58 Toán lớp 10: Cho tam giác ABC...
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vecto với một số
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vecto