Sách bài tập Toán 10 Bài 9 (Kết nối tri thức): Tích của một vectơ với một số

Nguyễn Thị Thuỳ Linh Ngày: 24-09-2024 Lớp 10

5 K

Với giải sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 9: Tích của một vectơ với một số

Giải SBT Toán 10 trang 54 Tập 1

Bài 4.13 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC. Gọi D, E tương ứng là trung điểm của BC, CA. Hãy biểu thị các vectơ $\vec{A B}, \vec{B C}, \vec{C A}$ theo hai vectơ $\vec{A D}$ và $\vec{B E}$

Lời giải:

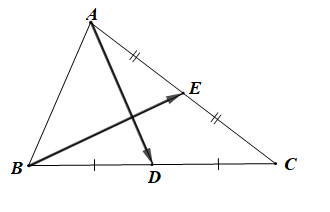
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Ta có:

+) D là trung điểm của BC nên $\vec{A B} + \vec{A C} = 2 \vec{A D}$

+) E là trung điểm của AC nên $\vec{A C} = 2 \vec{A E}$

Do đó

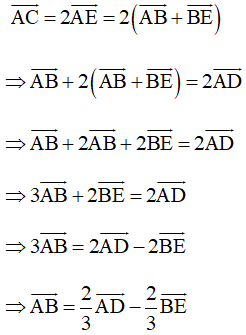
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

+) Vì $\vec{A B} + \vec{A C} = 2 \vec{A D}$ nên $\vec{A C} = 2 \vec{A D} - \vec{A B}$

Mà

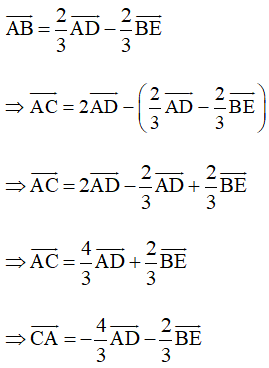
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

+) $\vec{B C} = \vec{A C} - \vec{A B}$ (quy tắc hiệu)

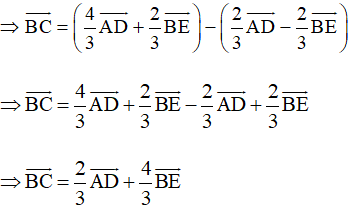
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Vậy $\vec{A B} = \frac{2}{3} \vec{A D} - \frac{2}{3} \vec{B E};$ $\vec{B C} = \frac{2}{3} \vec{A D} + \frac{4}{3} \vec{B E}$ và $\vec{C A} = - \frac{4}{3} \vec{A D} - \frac{2}{3} \vec{B E} .$

Bài 4.14 trang 54 SBT Toán 10 Tập 1: Cho tam giác OAB vuông cân, với OA = OB = a. Hãy xác định độ dài của các vectơ sau $\vec{O A} + \vec{O B},$ $\vec{O A} - \vec{O B},$ $\vec{O A} - \vec{O B},$ $2 \vec{O A} - 3 \vec{O B} .$

Lời giải:

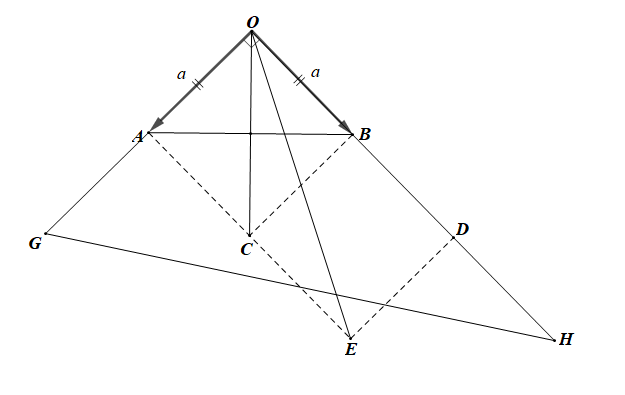
Gọi C là điểm thoả mãn OACB là hình bình hành

Mà ∆OAB vuông cân có OA = OB nên OACB là hình vuông

Þ OC = AB

Mà AB² = OA² + OB²(định lí Pythagoras)

Þ AB² = a² + a² = 2a²

$\Rightarrow O C = A B = a \sqrt{2}$

+) Có: $\vec{O A} + \vec{O B} = \vec{O C}$ (quy tắc hình bình hành)

$\Rightarrow |\vec{O A} + \vec{O B}| = |\vec{O C}| = O C = a \sqrt{2}$

+) Có:

$\vec{O A} - \vec{O B} = \vec{O A} + \vec{B O} = \vec{B O} + \vec{O A} = \vec{B A}$

$\Rightarrow |\vec{O A} + \vec{O B}| = |\vec{O C}| = O C = a \sqrt{2}$

+) Lấy điểm D sao cho $\vec{O D} = 2 \vec{O B}$ nên hai vectơ $\vec{O D}$ , $\vec{O B}$ cùng hướng và OD = 2OB.

Có: $\vec{O A} + 2 \vec{O B} = \vec{O A} + \vec{O D}$

Vẽ hình chữ nhật OAED, khi đó $\vec{O A} + \vec{O D} = \vec{O E}$

$\Rightarrow |\vec{O A} + 2 \vec{O B}| = |\vec{O E}| = O E$

Mà OE² = OD² + DE² (định lí Pythagoras)

Þ OE² = (2OB)² + OA²

Þ OE² = (2a)² + a² = 5a²

$\Rightarrow O E = a \sqrt{5}$

Do đó $|\vec{O A} + 2 \vec{O B}| = a \sqrt{5}$

+) Lấy điểm G sao cho $\vec{O G} = 2 \vec{O A}, \vec{O H} = 3 \vec{O B}$

Khi đó: hai vectơ $\vec{O G}$ , $\vec{O A}$ cùng hướng và OG = 2OA;

Và hai vectơ $\vec{O H}$ , $\vec{O B}$ cùng hướng và OH = 3OB.

Có: $2 \vec{O A} - 3 \vec{O B} = \vec{O G} - \vec{O H}$

$= \vec{O G} + \vec{H O}$ $= \vec{H O} + \vec{O G}$

$= \vec{H G}$

$\Rightarrow |2 \vec{O A} - 3 \vec{O B}| = |\vec{H G}| = H G$

Mà HG² = OG² + OH² (định lí Pythagoras)

Þ HG² = (2OA)² + (3OB)²

Þ HG² = (2a)² + (3a)²

Þ HG² = 13a²

$\Rightarrow H G = a \sqrt{13}$

Do đó $|2 \vec{O A} - 3 \vec{O B}| = a \sqrt{13} .$

Vậy $|\vec{O A} + \vec{O B}| = a \sqrt{2};$ $|\vec{O A} - \vec{O B}| = a \sqrt{2};$ $|\vec{O A} + 2 \vec{O B}| = a \sqrt{5}$ và $|2 \vec{O A} - 3 \vec{O B}| = a \sqrt{13} .$

Bài 4.15 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O.

a) Gọi M là trung điểm của BC. Chứng minh rằng $\vec{A H} = 2 \vec{O M} .$

b) Chứng minh rằng $\vec{O A} + \vec{O B} + \vec{O C} = \vec{O H} .$

c) Chứng minh rằng ba điểm G, H, O cùng thuộc một đường thẳng.

Lời giải:

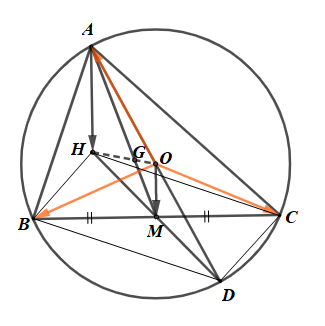
a) Kẻ đường kính AD.

Hai điểm B, C thuộc đường tròn đường kính AD nên $\hat{A B D} = \hat{A C D} = 90 °$

Hay BD ⊥ AB, CD ⊥ AC

Lại có H là trực tâm ∆ABC nên BH ⊥ AC, CH ⊥ AB

Þ BH /// CD và CH // BD

Þ BHCD là hình bình hành (dấu hiệu nhận biết)

Þ Hai đường chéo cắt nhau tại trung điểm của mỗi đường (tính chất hình bình hành)

Mà M là trung điểm của BC

Þ M là trung điểm của HD

Mà O là trung điểm của AD

Khi đó OM là đường trung bình của ∆AHD

Þ OM // AH và $A H = 2. O M$ (tính chất đường trung bình)

Do đó hai vectơ $\vec{A H}$ và $\vec{O M}$ có:

+ Cùng phương, cùng hướng

+ Độ dài: $|\vec{A H}| = 2 |\vec{O M}|$

$\Rightarrow \vec{A H} = 2 \vec{O M} .$

Vậy $\vec{A H} = 2 \vec{O M} .$

b) Vì M là trung điểm của BC nên $\vec{O B} + \vec{O C} = 2 \vec{O M}$

Mà $\vec{A H} = 2 \vec{O M}$ (câu a)

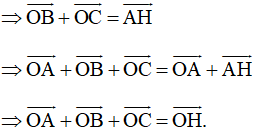
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Vậy $\vec{O A} + \vec{O B} + \vec{O C} = \vec{O H} .$

c) Vì G là trọng tâm tam giác ABC nên $\vec{O A} + \vec{O B} + \vec{O C} = 3 \vec{O G} .$

Mà $\vec{O A} + \vec{O B} + \vec{O C} = \vec{O H}$ (câu b)

Suy ra $\vec{O H} = 3 \vec{O G}$

Khi đó $\vec{O H}$ và $\vec{O G}$ cùng phương, cùng hướng

Þ O, H, G thẳng hàng.

Vậy ba điểm O, H, G thẳng hàng.

Bài 4.16 trang 54 SBT Toán 10 Tập 1: Cho tứ giác ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD và gọi I là trung điểm của MN. Chứng minh rằng với điểm O bất kì đều có

$\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = 4 \vec{O I} .$

Lời giải:

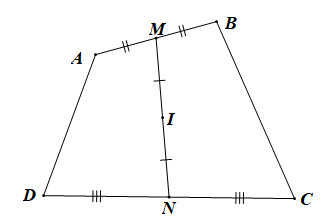
Với điểm O bất kì ta có:

+) $\vec{O A} + \vec{O B} = 2 \vec{O M}$ (do M là trung điểm của AB)

+) $\vec{O C} + \vec{O D} = 2 \vec{O N}$ (do N là trung điểm của CD)

+) $\vec{O M} + \vec{O N} = 2 \vec{O I}$ (do I là trung điểm của MN)

Þ $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = 2 \vec{O M} + 2 \vec{O N}$

$= 2 (\vec{O M} + \vec{O N}) = 2.2 \vec{O I} = 4 \vec{O I}$

Vậy với điểm O bất kì đều có: $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = 4 \vec{O I} .$

Bài 4.17 trang 54 SBT Toán 10 Tập 1: Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Lời giải:

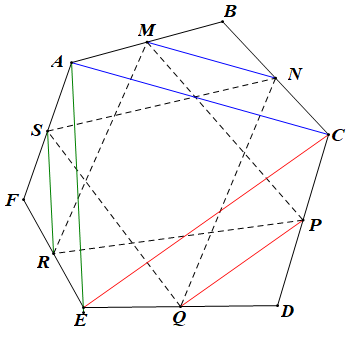
+) Vì M, N lần lượt là trung điểm của AB, BC

Nên MN là đường trung bình của tam giác ABC.

Þ MN // AC và $M N = \frac{1}{2} A C$ (tính chất đường trung bình)

Do đó $\vec{M N} = \frac{1}{2} \vec{A C}$ (1)

Chứng minh tương tự ta cũng có: $\vec{P Q} = \frac{1}{2} \vec{C E}$ (2)

Và $\vec{R S} = \frac{1}{2} \vec{E A}$ (3)

Từ (1), (2) và (3) ta có:

$\vec{M N} + \vec{P Q} + \vec{R S} = \frac{1}{2} \vec{A C} + \frac{1}{2} \vec{C E} + \frac{1}{2} \vec{E A}$

$= \frac{1}{2} (\vec{A C} + \vec{C E} + \vec{E A})$

$= \frac{1}{2} (\vec{A E} + \vec{E A})$ (quy tắc ba điểm)

$= \frac{1}{2} \vec{AA}$ (quy tắc ba điểm)

$= \frac{1}{2} . \vec{0} = \vec{0}$

Do đó $\vec{M N} + \vec{P Q} + \vec{R S} = \vec{0}$

+) Giả sử G và G' lần lượt là trọng tâm của tam giác MPR và tam giác NQS.

Khi đó ta có: $\vec{M G} + \vec{P G} + \vec{R G} = \vec{0}$ và $\vec{N G^{'}} + \vec{Q G^{'}} + \vec{S G^{'}} = \vec{0}$ hay $\vec{G^{'} N} + \vec{G^{'} Q} + \vec{G^{'} S} = \vec{0}$

Mặt khác: theo quy tắc ba điểm ta có:

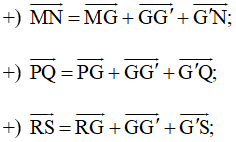
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

$\Rightarrow \vec{M N} + \vec{P Q} + \vec{R S} = \vec{M G} + \vec{P G} + \vec{R G} + 3. \vec{G G^{'}} + \vec{G^{'} N} + \vec{G^{'} Q} + \vec{G^{'} S}$

$= (\vec{M G} + \vec{P G} + \vec{R G}) + 3. \vec{G G^{'}} + (\vec{G^{'} N} + \vec{G^{'} Q} + \vec{G^{'} S})$

$= \vec{0} + 3. \vec{G G^{'}} + \vec{0}$

$= 3. \vec{G G^{'}}$

+) Lại có $\vec{M N} + \vec{P Q} + \vec{R S} = \vec{0}$ (chứng minh trên)

Nên $3 \vec{G G^{'}} = \vec{0}$

$\Rightarrow \vec{G G^{'}} = \vec{0}$

Suy ra G và G' trùng nhau.

Vậy hai tam giác MPR và NQS có cùng trọng tâm.

Bài 4.18 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC đều với trọng tâm O. M là một điểm tuỳ ý nằm trong tam giác. Gọi D, E, F theo thứ tự là hình chiếu vuông góc của M trên BC, CA, AB.

Chứng minh rằng $\vec{M D} + \vec{M E} + \vec{M F} = \frac{3}{2} \vec{M O} .$

Lời giải:

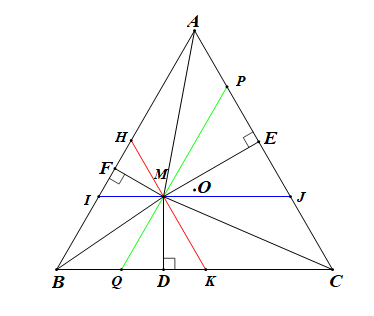
Qua M, kẻ các đường thẳng IJ // BC, HK // AC, PQ // AB.

Tam giác ABC đều nên $\hat{A B C} = \hat{A C B} = 60 °$

Mà PQ // AB nên $\hat{M Q K} = \hat{A B C} = 60 °,$

HK // AC nên $\hat{M K Q} = \hat{A C B} = 60 °$

Tam giác MQK có: $\hat{M Q K} = \hat{M K Q} = 60 °$ nên là tam giác đều.

Lại có MD là đường cao kẻ từ M nên MD đồng thời là đường trung tuyến

Do đó D là trung điểm của QK

$\Rightarrow \vec{M Q} + \vec{M K} = 2 \vec{M D}$ (1)

Chứng minh tương tự ta cũng có:

+) $\vec{M H} + \vec{M I} = 2 \vec{M F}$ (2)

+) $\vec{M P} + \vec{M J} = 2 \vec{M E}$ (3)

Từ (1), (2) và (3) ta có:

$\vec{M Q} + \vec{M K} + \vec{M H} + \vec{M I} + \vec{M P} + \vec{M J} = 2 \vec{M D} + 2 \vec{M F} + 2 \vec{M E}$

$\Rightarrow 2 (\vec{M D} + \vec{M F} + \vec{M E}) = (\vec{M Q} + \vec{M I})$ $+ (\vec{M K} + \vec{M J}) + (\vec{M H} + \vec{M P})$

Vì MI // BQ, MQ // BI nên tứ giác MIBQ là hình bình hành

$\Rightarrow \vec{M I} + \vec{M Q} = \vec{M B}$

Tương tự ta có $\vec{M K} + \vec{M J} = \vec{M C}; \vec{M H} + \vec{M P} = \vec{M A}$

Khi đó

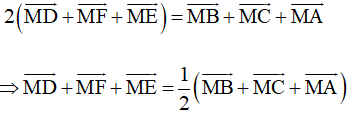
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Lại có O là trọng tâm của tam giác ABC nên $\vec{M B} + \vec{M C} + \vec{M A} = 3 \vec{M O}$

$\Rightarrow \vec{M D} + \vec{M F} + \vec{M E} = \frac{1}{2} .3 \vec{M O} = \frac{3}{2} \vec{M O} .$

Vậy $\vec{M D} + \vec{M E} + \vec{M F} = \frac{3}{2} \vec{M O} .$

Bài 4.19 trang 54 SBT Toán 10 Tập 1: Cho tam giác ABC.

a) Tìm điểm M sao cho $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0} .$

b) Xác định điểm N thoả mãn $4 \vec{N A} - 2 \vec{N B} + \vec{N C} = \vec{0} .$

Lời giải:

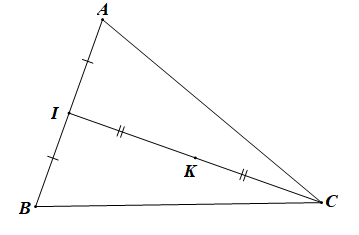
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Gọi I là trung điểm của AB.

Khi đó: $\vec{M A} + \vec{M B} = 2 \vec{M I}$

$\Rightarrow \vec{M A} + \vec{M B} + 2 \vec{M C} =$ $2 \vec{M I} + 2 \vec{M C} = 2 (\vec{M I} + \vec{M C})$

Gọi K là trung điểm của IC, khi đó: $\vec{M I} + \vec{M C} = 2 \vec{M K}$

$\Rightarrow \vec{M A} + \vec{M B} + 2 \vec{M C} = 2.2 \vec{M K} = 4 \vec{M K} .$

Mà $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0} .$

Do đó $4 \vec{M K} = \vec{0} \Leftrightarrow \vec{M K} = \vec{0}$

Suy ra M ≡ K.

Vậy M là trung điểm của IC (với I là trung điểm của AB).

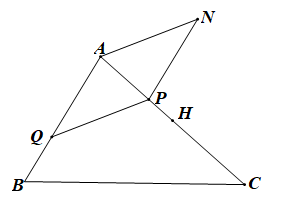
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Ta có:

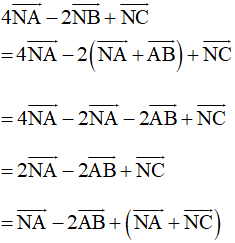
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Gọi H là trung điểm của AC, khi đó

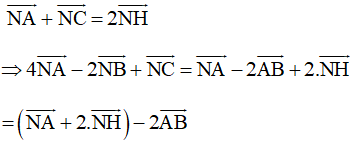
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Giả sử P là điểm thỏa mãn $\vec{P A} + 2. \vec{P H} = \vec{0}$

Khi đó

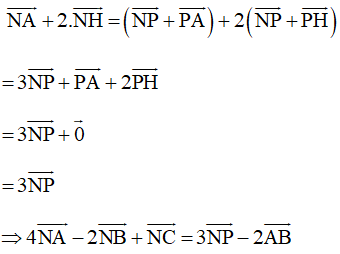
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Mà $4 \vec{N A} - 2 \vec{N B} + \vec{N C} = \vec{0} .$

Nên

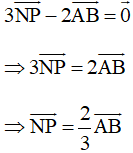
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Gọi Q là điểm nằm trên cạnh AB sao cho $\vec{A Q} = \frac{2}{3} \vec{A B}$

$\Rightarrow \vec{N P} = \vec{A Q}$

Do đó tứ giác AQPN là hình bình hành

Vậy điểm N cần tìm là đỉnh của hình bình hành AQPN (với Q thỏa mãn $\vec{A Q} = \frac{2}{3} \vec{A B}$ và P thỏa mãn $\vec{P A} + 2. \vec{P H} = \vec{0}$ , H là trung điểm của AC).

Giải SBT Toán 10 trang 55 Tập 1

Bài 4.20 trang 55 SBT Toán 10 Tập 1: Cho tam giác ABC.

a) Tìm điểm K thoả mãn $\vec{K A} + 2 \vec{K B} + 3 \vec{K C} = \vec{0} .$

b) Tìm tập hợp các điểm M thoả mãn $|\vec{M A} + \vec{2 M B} + 3 \vec{M C}| = |\vec{M B} - \vec{M C}| .$

Lời giải:

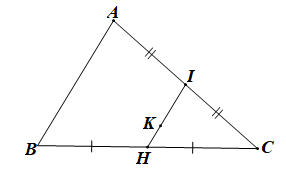
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Gọi I là trung điểm của AC, H là trung điểm của BC.

Khi đó $\vec{K A} + \vec{K C} = 2 \vec{K I}$ và $\vec{K B} + \vec{K C} = 2 \vec{K H}$

$\Rightarrow \vec{K A} + 2 \vec{K B} + 3 \vec{K C}$ $= (\vec{K A} + \vec{K C}) + 2 (\vec{K B} + \vec{K C})$

$= 2 \vec{K I} + 2.2 \vec{K H}$ $= 2 \vec{K I} + 4 \vec{K H}$

Mà $\vec{K A} + 2 \vec{K B} + 3 \vec{K C} = \vec{0} .$

Nên

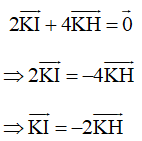
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Khi đó $\vec{K I}$ và $\vec{K H}$ là hai vectơ cùng phương, ngược hướng và $|\vec{K I}| = 2 |\vec{K H}|$

Do đó điểm K nằm giữa hai điểm I và H sao cho KI = 2KH.

Vậy ta có điểm K thỏa mãn $\vec{K A} + 2 \vec{K B} + 3 \vec{K C} = \vec{0}$ như hình vẽ.

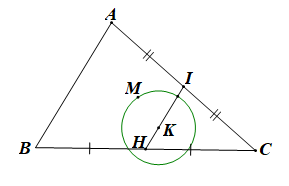
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Chứng minh tương tự câu a ta có:

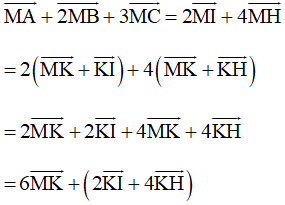
Sách bài tập Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức (ảnh 1)

Mà $2 \vec{K I} + 4 \vec{K H} = \vec{0}$ (câu a)

Nên $\vec{M A} + \vec{2 M B} + 3 \vec{M C} = 6 \vec{M K}$

Lại có: $\vec{M B} - \vec{M C} = \vec{C B}$

Do đó $|\vec{M A} + \vec{2 M B} + 3 \vec{M C}| = |\vec{M B} - \vec{M C}| .$

$\Leftrightarrow |6 \vec{M K}| = |\vec{C B}|$

Û 6MK = CB

$\Leftrightarrow K M = \frac{B C}{6}$

Do đó tập hợp điểm M là đường tròn tâm K, bán kính bằng $\frac{B C}{6}$ như hình vẽ.

Bài 4.21 trang 55 SBT Toán 10 Tập 1: Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực $\vec{P}$ của vật và lực đẩy Archimedes $\vec{F}$ mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng.

Lời giải:

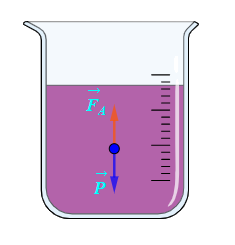
Trọng lực $\vec{P}$ của vật và lực đẩy Archimedes $\vec{F}$ mà chất lỏng tác động lên vật được mô tả như hình vẽ trên.

Do vật ở trạng thái cân bằng nên hai lực $\vec{P}$ và $\vec{F}$ ngược hướng nhau và có cường độ bằng nhau.

$\Rightarrow |\vec{P}| = |\vec{F}|$

Gọi d và d' là trọng lượng riêng của vật và chất lỏng;

V là thể tích của vật

Khi thả vật vào cốc chất lỏng thì ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng nên thể tích chất lỏng bị chiếm chỗ là $\frac{V}{2} .$

Khi đó trọng lượng của vật là: P = d.V

Và lực đẩy Archimedes mà chất lỏng tác động lên vật là: $F_{A} = d^{'} . \frac{V}{2} .$

Do đó

$|\vec{P}| = |\vec{F}| \Leftrightarrow d . V = d^{'} . \frac{V}{2} \Leftrightarrow d = \frac{d^{'}}{2} \Leftrightarrow \frac{d}{d^{'}} = \frac{1}{2} .$

Vậy tỉ số giữa trọng lượng riêng của vật và của chất lỏng bằng $\frac{1}{2}$

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu của hai vectơ

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Lý thuyết Tích của một vectơ với một số

1. Tích của một vectơ với một số

• Tích của một vectơ $\vec{a} \neq \vec{0}$ với một số thực k > 0 là một vectơ, kí hiệu là k $\vec{a}$ , cùng hướng với vectơ $\vec{a}$ và có độ dài bằng k $\vec{a}$ .

Ví dụ: Cho hình vẽ sau:

Tích của một vectơ với một số

– Vectơ $\frac{1}{2} \vec{a}$ cùng hướng với vectơ $\vec{a}$ và $(\frac{1}{2} \vec{a})$ = $\frac{1}{2} | \vec{a} |$

– Vectơ $\frac{3}{2} \vec{a}$ cùng hướng với vectơ $\vec{a}$ và $(\frac{3}{2} \vec{a})$ = $\frac{3}{2} | \vec{a} |$ .

• Tích của một vectơ $\vec{a} \neq \vec{0}$ với một số thực k < 0 là một vectơ, kí hiệu là k $\vec{a}$ , ngược hướng với vectơ $\vec{a}$ và có độ dài bằng (–k) | $\vec{a}$ |.

Ví dụ: Cho hình sau:

Tích của một vectơ với một số

– Vectơ –2 $\vec{a}$ ngược hướng với vectơ $\vec{a}$ và $(- 2 \vec{a})$ = $2 | \vec{a} |$

– Vectơ $- \frac{3}{2} \vec{a}$ ngược hướng với vectơ $\vec{a}$ và $(- \frac{3}{2} \vec{a})$ = $\frac{3}{2} | \vec{a} |$ .

Chú ý: Ta quy ước k $\vec{a}$ = $\vec{0}$ nếu $\vec{a}$ = $\vec{0}$ hoặc k = 0.

Nhận xét: Vectơ k $\vec{a}$ có độ dài bằng |k|| $\vec{a}$ | và cùng hướng với $\vec{a}$ nếu k ≥ 0, ngược hướng với $\vec{a}$ nếu $\vec{a}$ ≠ $\vec{0}$ và k < 0.

Chú ý: Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với một số (hay phép nhân một số với vectơ).

2. Các tính chất của phép nhân vectơ với một số

Với hai vectơ $\vec{a}$ , $\vec{b}$ và hai số thực k, t, ta luôn có :

+) k(t $\vec{a}$ ) = (kt) $\vec{a}$ ;

+) k ( $\vec{a}$ + $\vec{b}$ ) = k $\vec{a}$ + k $\vec{b}$ ; k ( $\vec{a}$ – $\vec{b}$ ) = k $\vec{a}$ – k $\vec{b}$ ;

+) (k + t) $\vec{a}$ = k $\vec{a}$ + t $\vec{a}$ ;

+) 1 $\vec{a}$ = $\vec{a}$ ; (–1) $\vec{a}$ = – $\vec{a}$ .

Nhận xét:

Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{I A} + \vec{I B} = \vec{0}$ .

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

Ví dụ:

a) Cho đoạn thẳng CD có trung điểm I. Chứng minh với điểm O tùy ý, ta có $\vec{O C} + \vec{O D} = 2 \vec{O I}$ .

b) Cho tam giác ABC có G là trọng tâm. Chứng minh rằng với điểm O tùy ý, ta có $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = 3 \vec{O G}$ .

Hướng dẫn giải

a) Vì I là trung điểm của CD nên ta có $\vec{I C} + \vec{I D} = \vec{0}$ .

Do đó $\vec{O C} + \vec{O D} = (\vec{O I} + \vec{I C}) + (\vec{O I} + \vec{I D})$ = 2 $\vec{O I}$ + ( $\vec{I C} + \vec{I D}$ )= 2 $\vec{O I}$ + $\vec{0}$ = 2 $\vec{O I}$ .

Vậy, $\vec{O C} + \vec{O D} = 2 \vec{O I}$ .

b) Vì G là trọng tâm tam giác ABC nên: $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

Ta có $\vec{O A} + \vec{O B} + \vec{O C} = (\vec{O G} + \vec{G A}) + (\vec{O G} + \vec{G B}) + (\vec{O G} + \vec{G C})$

= $3 \vec{O G} + (\vec{G A} + \vec{G B} + \vec{G C}) = 3 \vec{O G} + \vec{0} = 3 \vec{O G}$

Vậy $\vec{O A} + \vec{O B} + \vec{O C} = 3 \vec{O G}$ .

Chú ý : Cho hai vectơ không cùng phương $\vec{a}$ và $\vec{b}$ . Khi đó, mọi vectơ $\vec{u}$ đều biểu thị (phân tích) được một cách duy nhất theo hai vectơ $\vec{a}$ và $\vec{b}$ , nghĩa là có duy nhất cặp số (x; y) sao cho $\vec{u}$ = x $\vec{a}$ + y $\vec{b}$ .