Với giải Bài 5 trang 82 Toán lớp 10 Cánh diều chi tiết trong Bài 3: Khái niệm vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 3: Khái niệm vectơ
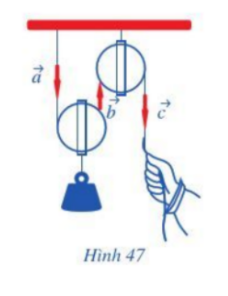
Bài 5 trang 82 Toán lớp 10: Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ (Hình 47).
a) Hãy chỉ ra các cặp vectơ cùng phương.
b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.
Phương pháp giải:
a) Bước 1: Xác định giá của các vectơ . Từ đó suy ra các vectơ cùng phương.
Bước 2: Kết luận các cặp vectơ cùng phương.
b) Nhận xét về hướng của 3 vectơ . Từ đó suy ra các cặp vectơ đó cùng hướng hay ngược hướng.
Lời giải:
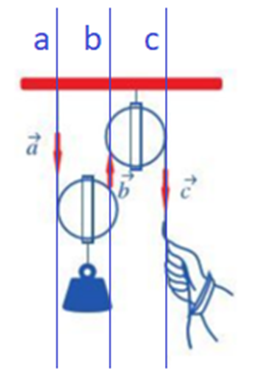
Gọi a, b, c là các đường thẳng lần lượt chứa các vectơ .
Khi đó: a, b, c lần lượt là giá của các vectơ
a) Dễ thấy: a // b // c
Ba vectơ cùng phương với nhau.
Vậy các cặp vectơ cùng phương là: và , và , và .
b) Quan sát ba vectơ, ta thấy: vectơ và cùng hướng xuống còn vectơ hướng lên trên.
Vậy vectơ và cùng hướng, vectơ và ngược hướng, vectơ và ngược hướng.
Bài tập vận dụng:
Bài 1. Cho hình vẽ sau. Hãy liệt kê các cặp vectơ cùng hướng và các cặp vectơ ngược hướng.
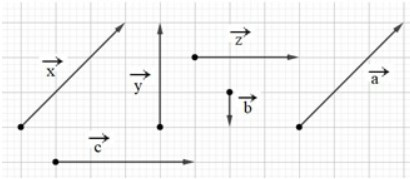
Hướng dẫn giải:
Ta có:
– Giá của vectơ và song song với nhau, đồng thời hai vectơ cùng chiều nên và là hai vectơ cùng hướng.
– Giá của vectơ và song song với nhau, đồng thời hai vectơ cùng chiều từ trái sang phải nên và là hai vectơ cùng hướng.
– Vectơ và song song với nhau nhưng ngược chiều nhau nên và là hai vectơ ngược hướng.
Bài 2. Trên hình vẽ sau cho các đoạn thẳng AB = 9, CD = 7, MN = 9, PQ = 7, HK = 7. Các vectơ nào bằng nhau?
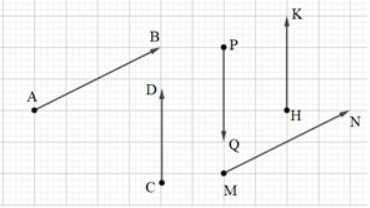
Hướng dẫn giải:
Ta có:
– Vectơ và có giá song song và cùng chiều nên hai vectơ và cùng hướng, đồng thời AB = MN = 9 nên = .
– Vectơ và có giá song song và cùng chiều nên hai vectơ và cùng hướng, mà HK = CD = 7 nên = .
Bài 3. Cho điểm A và vectơ khác vectơ . Xác định điểm M sao cho vectơ cùng phương với vectơ .
Hướng dẫn giải:
Gọi giá của vectơ là đường thẳng Δ.
TH1: Điểm A thuộc đường thẳng Δ.
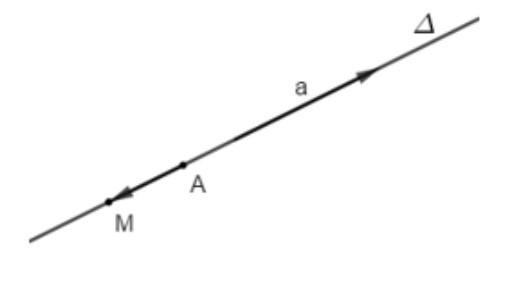
Lấy điểm M bất kỳ thuộc đường thẳng Δ.
Khi đó đường thẳng AM nằm trên đường thẳng Δ.
Suy ra vectơ cùng phương với vectơ .
Vậy M thuộc đường thẳng Δ với Δ đi qua điểm A và Δ là giá của vectơ .
TH2: Điểm A không thuộc đường thẳng Δ.
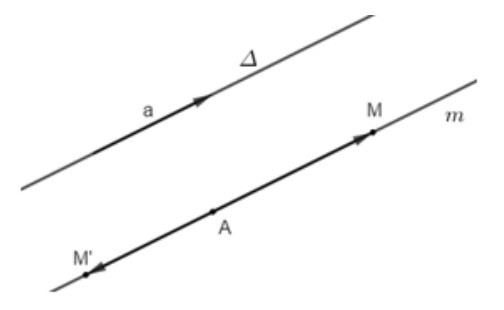
+ Qua A, dựng đường thẳng m song song với đường thẳng Δ.
+ Lấy điểm M bất kỳ thuộc đường thẳng m, khi đó AM // Δ.
Suy ra vectơ cùng phương với vectơ .
Vậy điểm M thuộc đường thẳng m đi qua A và m // Δ thì vectơ cùng phương với vectơ .
Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:
Hoạt động 2 trang 80 Toán lớp 10: Quan sát Hình 39 và cho biết vị trí tương đối giữa giá của vectơ...
Hoạt động 3 trang 80 Toán lớp 10: Quan sát hai biển báo ở Hình 40a, 40b, cho biết hai vectơ...
Hoạt động 4 trang 81 Toán lớp 10: Quan sát hai vectơ...
Luyện tập vận dụng 2 trang 81 Toán lớp 10: Cho tam giác ABC. Vẽ điểm D thỏa mãn...
Bài 1 trang 82 Toán lớp 10: Cho A, B, C là ba điểm thẳng hàng, B nằm giữa A và C....
Bài 2 trang 82 Toán lớp 10: Cho đoạn thẳng MN có trung điểm là I....
Bài 3 trang 82 Toán lớp 10: Cho hình thang ABCD có hai đáy là AB và CD. Tìm vectơ:...
Bài 4 trang 82 Toán lớp 10: Cho hình vuông ABCD có độ dài cạnh bằng 3cm....
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ
Bài 6: Tích vô hướng của hai vectơ