Với giải sách bài tập Toán 10 Bài 3: Khái niệm vectơ sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 3: Khái niệm vectơ

Giải SBT Toán 10 trang 85 Tập 1

Bài 22 trang 85 SBT Toán 10 Tập 1: Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn $\overrightarrow{AM}$ ngược hướng với $\overrightarrow{AB}$ là hình gì?

A. Đường thẳng AB.

B. Tia AB.

C. Tia đối của tia AB trừ điểm A.

D. Đoạn thẳng AB.

Lời giải:

Đáp án đúng là C

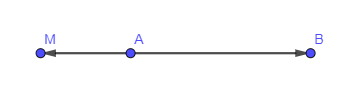
Ta có vectơ $\overrightarrow{AM}$ ngược hướng với vectơ $\overrightarrow{AB}$nên A, M, B thẳng hàng và M khác phía với B so với A.

Do đó tập hợp điểm M là tia đối của tia AB trừ đi điểm A.

Bài 23 trang 85 SBT Toán 10 Tập 1: Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn $\left|\overrightarrow{AM}\right|=\left|\overrightarrow{AB}\right|$ là hình gì?

A. Đường trung trực của đoạn thẳng AB.

B. Đường tròn tâm A bán kính AB.

C. Đường tròn tâm B bán kính AB.

D. Đoạn thẳng AB.

Lời giải:

Đáp án đúng là B

Ta có: $\left|\overrightarrow{AM}\right|=\left|\overrightarrow{AB}\right|$ 

Điểm M là điểm thỏa mãn độ dài vectơ $\overrightarrow{AM}$ bằng độ dài vectơ $\overrightarrow{AB}$ nghĩa là điểm M cách A một khoảng không đổi bằng độ dài vectơ $\overrightarrow{AB}$ là đường tròn tâm A bán kính AB.

Bài 24 trang 85 SBT Toán 10 Tập 1: Cho hình thang ABCD có AB và CD song song với nhau. Phát biểu nào dưới đây là đúng?

A. $\overrightarrow{AB}=\overrightarrow{CD}$.

B. $\overrightarrow{AB}$ và $\overrightarrow{DC}$ cùng hướng.

C. $\overrightarrow{AB}$ và $\overrightarrow{DC}$ ngược hướng.

D. $\overrightarrow{AB}=\overrightarrow{DC}$.

Lời giải:

Đáp án đúng là B

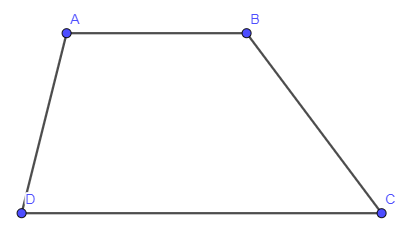
Vì ABCD là hình thang và AB // CD nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{DC}$ cùng hướng.

Bài 25 trang 85 SBT Toán 10 Tập 1: Cho $\overrightarrow{a}=\overrightarrow{b}$. Phát biểu nào dau đây là sai?

A. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng.

B. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng độ dài.

C. $\overrightarrow{a}$ và $\overrightarrow{b}$ không cùng phương.

D. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương.

Lời giải:

Đáp án đúng là C

Ta có $\overrightarrow{a}=\overrightarrow{b}$ thì $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng và cùng độ dài.

Vì $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng nên $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương.

Do đó A, B, D đúng và C sai.

Bài 26 trang 85 SBT Toán 10 Tập 1: Cho điểm I là trung điểm của đoạn thẳng AB. Phát biểu nào sau đây là đúng?

A. $\overrightarrow{IA}=\overrightarrow{IB}$.

B. $\overrightarrow{IA}$ và $\overrightarrow{IB}$ cùng hướng.

C. $\overrightarrow{AI}=\overrightarrow{BI}$.

D. $\overrightarrow{AI}=\overrightarrow{IB}$

Lời giải:

Đáp án đúng là D

I là trung điểm của AB nên IA = IB.

Hơn nữa ta thấy vectơ $\overrightarrow{IA}$ và vectơ $\overrightarrow{IB}$ cùng phương và ngược hướng nên $\overrightarrow{IA}=-\overrightarrow{IB}$ hay $\overrightarrow{AI}=\overrightarrow{IB}$.

Bài 27 trang 85 SBT Toán 10 Tập 1: Cho năm điểm A, B, C, D, E.

a) Viết các vectơ khác $\overrightarrow{0}$ có cùng điểm đầu là A, điểm cuối là một trong các điểm đã cho.

b) Viết các vectơ khác $\overrightarrow{0}$ có cùng điểm cuối là B, điểm đầu là một trong các điểm đã cho.

Lời giải:

a) Các vectơ khác $\overrightarrow{0}$ có cùng điểm đầu là A, điểm cuối là một trong các điểm đã cho là: $\overrightarrow{\text{AA}},\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD},\overrightarrow{AE}$.

b) Các vectơ khác $\overrightarrow{0}$ có cùng điểm cuối là B, điểm đầu là một trong các điểm đã cho là: $\overrightarrow{AB},\overrightarrow{BB},\overrightarrow{CB},\overrightarrow{DB},\overrightarrow{EB}$.

Bài 28 trang 85 SBT Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a. Tính $\left|\overrightarrow{AB}\right|,\left|\overrightarrow{AC}\right|$.

Lời giải:

Vì ABCD là hình vuông cạnh a nên $\left|\overrightarrow{AB}\right|=a$.

Xét tam giác ABC vuông tại B, có:

AC² = AB² + BC²

⇔ AC² = a² + a²

⇔ AC² = 2a²

⇔ AC = $\sqrt{2}$a.

⇒ $\left|\overrightarrow{AC}\right|=\sqrt{2}a$.

Vậy $\left|\overrightarrow{AB}\right|=a$ và  $\left|\overrightarrow{AC}\right|=\sqrt{2}a$.

Bài 29 trang 85 SBT Toán 10 Tập 1: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm BC, CA, AB. Chứng minh rằng:

a) $\overrightarrow{MN}=\overrightarrow{PA}$.

b) $\overrightarrow{MP}=\overrightarrow{CN}$.

Lời giải:

a) Xét tam giác ABC, có:

M là trung điểm của BC

N là trung điểm của AC

⇒ MN là đường trung bình của tam giác ABC

⇒ MN // BC và MN = $\frac{1}{2}$BC

Mà PA = PB = $\frac{1}{2}$BC

⇒ PA = MN

Vì MN // BC nên hai vectơ $\overrightarrow{MN}$ và $\overrightarrow{PA}$ cùng phương, cùng hướng và PA = MN. Do đó $\overrightarrow{MN}=\overrightarrow{PA}$.

b) Xét tam giác ABC, có:

M là trung điểm của BC

P là trung điểm của AB

⇒ MP là đường trung bình của tam giác ABC

⇒ MP // AC và MP = $\frac{1}{2}$AC

Mà CN = AN = $\frac{1}{2}$AC

⇒ MP = CN

Vì MP // AC nên hai vectơ $\overrightarrow{MP}$ và $\overrightarrow{AC}$ cùng phương, cùng hướng và MP = CN. Do đó $\overrightarrow{MP}=\overrightarrow{CN}$.

Giải SBT Toán 10 trang 86 Tập 1

Bài 30 trang 86 SBT Toán 10 Tập 1: Trong mặt phẳng nghiêng không có ma sát cho hệ vật m₁, m₂, hai vật nối với nhau bằng một sợi dây không dãn vắt qua ròng rọc (Hình 32). Giả sử bỏ qua khối lượng của dây và ma sát của ròng rọc.

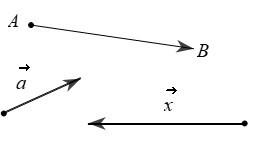
a) Tìm các cặp vec tơ cùng phương trong các cặp vectơ ở Hình 32.

b) Những cặp vectơ cùng phương đó có cùng hướng không?

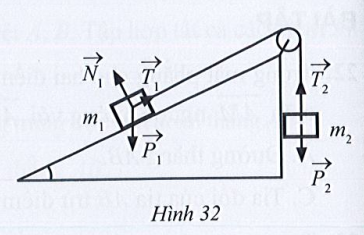
Lời giải:

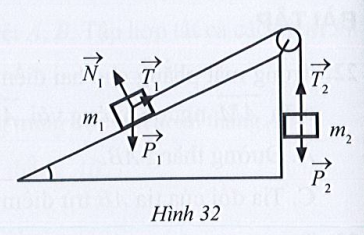
Các cặp vectơ cùng phương là: 

Bài 31* trang 86 SBT Toán 10 Tập 1: Cho đường tròn tâm O và dây cung BC không đi qua O. Điểm A chuyển động trên cung lớn BC của đường tròn sao cho tam giác ABC nhọn. Gọi H là trực tâm của tam giác ABC. Chứng minh rằng $\overrightarrow{AH}$ có độ dài không đổi.

Lời giải:

Kẻ đường kính AK (K ∈ (O)), gọi M là trung điểm của BC.

Vì H là trực tâm nên BH ⊥ AC, KC ⊥ AC ($\widehat{ACK}$ là góc nội tiếp chắn nửa đường tròn)

⇒ BH // KC

Chứng minh tương tự ta được CH // BK (cùng ⊥ AB)

⇒ BHCK là hình bình hành

Ta có M là trung điểm BC nên M là trung điểm của HK

Xét tam giác AHK, có:

O là trung điểm AC

M là trung điểm HK

⇒ OM là đường trung bình của tam giác AHK

⇒ OM // AH và $OM=\frac{1}{2}AH$

Vì O và M cố định nên OM cố định đó đó AH không đổi.

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Lý thuyết Khái niệm vectơ

1. Khái niệm vectơ

Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểu đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.

Định nghĩa: Vectơ là một đoạn thẳng có hướng.

Vectơ có điểm đầu A, điểm cuối B được kí hiệu là $\overrightarrow{\mathrm{AB}}$ và đọc là “vectơ AB”. Để vẽ được vectơ $\overrightarrow{\mathrm{AB}}$ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.

Đối với vectơ $\overrightarrow{\mathrm{AB}}$, ta gọi:

– Đường thẳng d đi qua hai điểm A và B là giá của vectơ $\overrightarrow{\mathrm{AB}}$.

– Độ dài đoạn thẳng AB là độ dài của vectơ $\overrightarrow{\mathrm{AB}}$, kí hiệu là $\left|\overrightarrow{\mathrm{AB}}\right|$.

Vectơ còn được kí hiệu là $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, $\overrightarrow{\mathrm{x}}$, $\overrightarrow{\mathrm{y}}$ khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Độ dài của vectơ $\overrightarrow{\mathrm{a}}$ được kí hiệu là $\left|\overrightarrow{\mathrm{a}}\right|.$ 

Ví dụ: Vectơ $\overrightarrow{\mathrm{AB}}$ có độ dài là 5, ta có thể viết như sau: $\left|\overrightarrow{\mathrm{AB}}\right|$ = 5.

2. Vectơ cùng phương, vectơ cùng hướng

Định nghĩa:

– Hai vectơ cùng phương: Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Ví dụ:

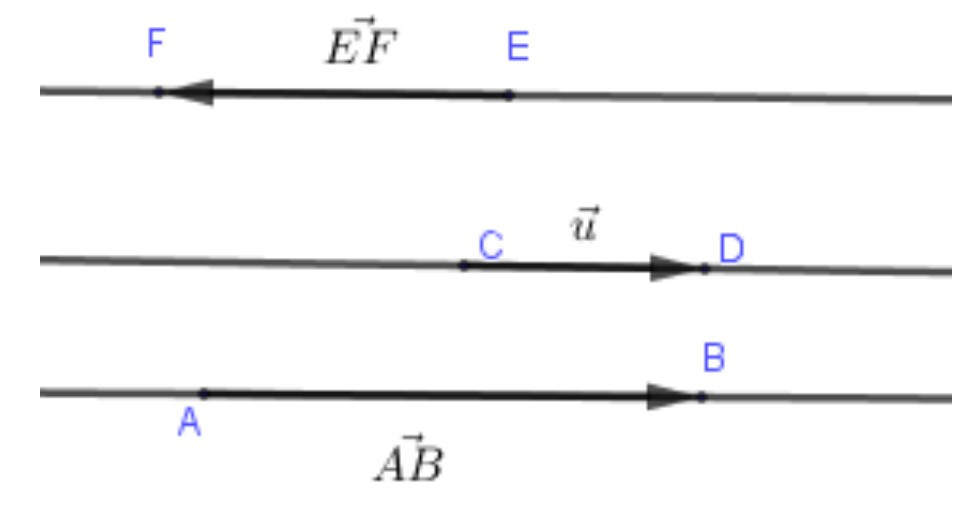
Trên hình vẽ các vectơ $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{CD}}$, $\stackrel{\rightharpoonup }{\mathrm{EF}}$ cùng phương với nhau.

Nhận xét: Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.

Ví dụ:

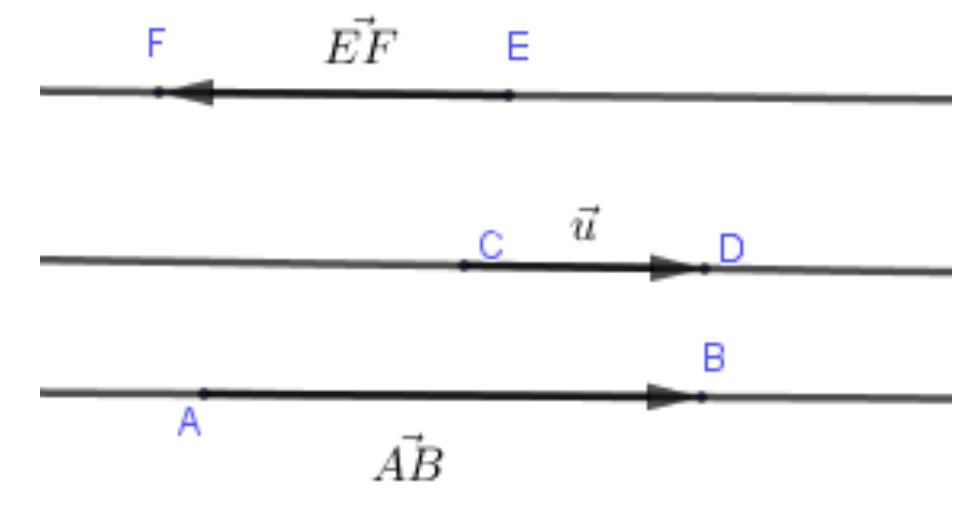
Hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{CD}}$cùng phương và có cùng hướng đi từ trái sang phải. Ta nói hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{CD}}$ cùng hướng. Hai vectơ $\overrightarrow{\mathrm{CD}}$ và $\stackrel{\rightharpoonup }{\mathrm{EF}}$cùng phương nhưng ngược hướng nhau. Ta nói hai vectơ $\overrightarrow{\mathrm{CD}}$ và $\stackrel{\rightharpoonup }{\mathrm{EF}}$ là hai vectơ ngược hướng.

Ví dụ: Cho hình bình hành ABCD. Liệt kê các cặp vectơ cùng hướng và ngược hướng trong hình bình hành ABCD. 

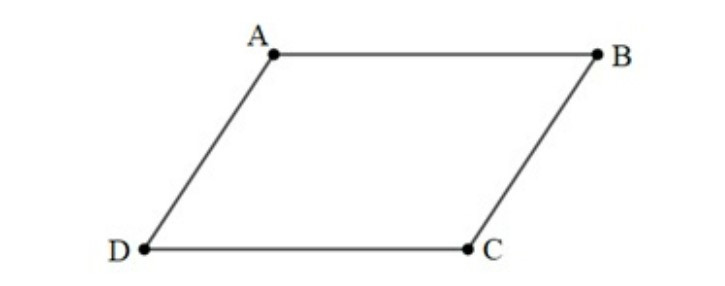
Hướng dẫn giải:

Do ABCD là hình bình hành nên ta có: AB // DC và AD // BC.

Các cặp vectơ cùng hướng: $\overrightarrow{\mathrm{AB}}$và $\overrightarrow{\mathrm{DC}}$, $\overrightarrow{\mathrm{AD}}$và $\overrightarrow{\mathrm{BC}}$, $\overrightarrow{\mathrm{BA}}$và $\overrightarrow{\mathrm{CD}}$, $\overrightarrow{\mathrm{DA}}$ và $\overrightarrow{\mathrm{CB}}$.

Các cặp vectơ ngược hướng: $\overrightarrow{\mathrm{AB}}$và $\overrightarrow{\mathrm{CD}}$, $\overrightarrow{\mathrm{AD}}$và $\overrightarrow{\mathrm{CB}}$, $\overrightarrow{\mathrm{BA}}$và $\overrightarrow{\mathrm{DC}}$, $\overrightarrow{\mathrm{DA}}$và $\overrightarrow{\mathrm{BC}}$.

3. Hai vectơ bằng nhau

Hai vectơ $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{CD}}$ bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{CD}}.$ 

Nhận xét:

– Hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{b}}$.

– Khi cho trước vectơ $\overrightarrow{\mathrm{a}}$ và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho $\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}}.$ 

Ví dụ: Cho hình bình hành ABCD, khi đó:

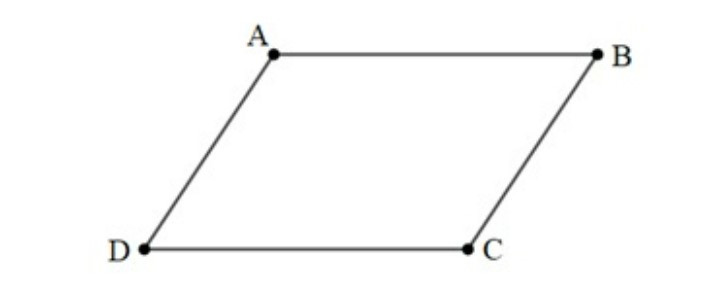
Do ABCD là hình bình hành nên ta có:

$\left\{\begin{array}{l}\mathrm{AB}//\mathrm{DC}\mathrm{và}\mathrm{AD}//\mathrm{BC}\\ \mathrm{AB}=\mathrm{CD}\mathrm{và}\mathrm{AD}=\mathrm{BC}\end{array}\right.$

Ta lại có: $\overrightarrow{\mathrm{AB}}$và $\overrightarrow{\mathrm{DC}}$ ; $\overrightarrow{\mathrm{AD}}$ và $\overrightarrow{\mathrm{BC}}$ là hai cặp vectơ cùng hướng nên $\left\{\begin{array}{l}\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DC}}\\ \overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{BC}}\end{array}\right.$.

4. Vectơ–không

Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.

Bây giờ với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là $\overrightarrow{\mathrm{AA}}$ và được gọi là vectơ – không.

Định nghĩa: Vectơ–không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là $\overrightarrow{0}.$

Ta quy ước $\overrightarrow{0}.$ cùng phương và cùng hướng với mọi vectơ và $\left|\overrightarrow{0}\right|$ = 0.

Nhận xét: Hai điểm A, B trùng nhau khi và chỉ khi $\overrightarrow{\mathrm{AB}}$= $\overrightarrow{0}$.

Ví dụ: Vectơ $\overrightarrow{\mathrm{BB}}$ là vectơ – không và $\left|\overrightarrow{\mathrm{BB}}\right|=0.$  

5. Biểu thị một số đại lượng có hướng bằng vectơ

Trong vật lý, một số đại lượng như trọng lực, vận tốc,… là đại lượng có hướng. Người ta dùng vectơ để biểu thị các đại lượng đó.

Ví dụ: Chọn trục tọa độ là trục Oy có chiều hướng lên trên, biểu điễn vectơ lực $\overrightarrow{\mathrm{F}}$ có điểm đặt tại gốc O trong hai trường hợp sau:

a) $\overrightarrow{\mathrm{F}}$ có phương thẳng đứng chiều hướng xuống

b) $\overrightarrow{\mathrm{F}}$ có phương thẳng đứng hướng lên trên

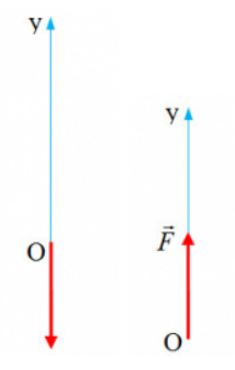
Ta thấy vectơ lực $\overrightarrow{\mathrm{F}}$ ở hai trường hợp cùng phương nhưng ngược hướng với nhau.