Với giải Khám phá 2 trang 85 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2: Tiếp tuyến của đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn

Khám phá 2 trang 85 Toán 9 Tập 1: Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).

a) Giải thích tại sao ta có OA = R và OM > R.

b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.

Lời giải:

a) Vì điểm A nằm trên đường tròn (O; R) nên OA = R.

Ta có OA vuông góc với đường thẳng d tại A nên OA là khoảng cách từ điểm O đến đường thẳng d.

Do OA, OM lần lượt là đường vuông góc, đường xiên kẻ từ O đến đường thẳng d nên OA < OM.

Mà OA = R nên OM > R.

b) Ta có OA = R nên d tiếp xúc với đường tròn (O; R) tại A.

Mà khi đường thẳng d tiếp xúc với đường tròn (O; R) thì đường thẳng d và đường tròn (O; R) có duy nhất một điểm chung.

Vậy d và (O) không thể có điểm chung nào khác ngoài A.

 Lý Thuyết Dấu hiệu nhận biết tiếp tuyến của đường tròn

Dấu hiệu nhận biết tiếp tuyến

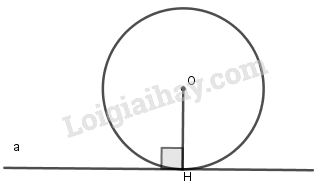
Tính chất của tiếp tuyến