Với giải sách bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 2: Tiếp tuyến của đường tròn
Bài 1 trang 88 sách bài tập Toán 9 Tập 1: Cho ba điểm A, B, C cùng nằm trên đường tròn (O) sao cho AC đi qua O. Vẽ đoạn thẳng DE tiếp xúc với (O) tại A. Cho biết Tính số đo
Lời giải:
Do DE tiếp xúc với (O) tại A, suy ra OA ⊥ DE tại A hay
Suy ra
Nên hay
Xét ∆ABC có BO là đường trung tuyến và nên ∆ABC vuông tại B.
Suy ra: (tổng hai góc nhọn của tam giác vuông bằng 90°)
Do đó
Bài 2 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). Cho biết PB = 8, PQ = 4. Tính R và số đo
Lời giải:
Do PB và PA là hai tiếp tuyến của đường tròn (O) lần lượt tại B và A
Suy ra OB ⊥ BP; OA ⊥ AP
Nên ∆OBP vuông tại B; ∆OAP vuông tại A.
Xét ∆OPB vuông tại B, ta có OP2 = OB2 + PB2 (định lí Pythagore)
Hay (OQ + QP)2 = OB2 + PB2
Suy ra (R + 4)2 = R2 + 82
R2 + 8R + 16 = R2 + 64
8R = 48
R = 6.
Do đó OP = OQ + QP = 6 + 4 = 10.
Như vậy, suy ra
Theo bài, hai tiếp tuyến AP và BP của đường tròn (O; R) cắt nhau tại P nên OP là tia phân giác của góc AOB.
Khi đó,
Bài 3 trang 89 sách bài tập Toán 9 Tập 1: Gọi d là khoảng cách từ điểm O đến đường thẳng a. Xác định vị trí tương đối của đường thẳng a và đường tròn (O; r) trong các trường hợp sau:
a) r = 5, d = 13;
b) r = 8, d = 8;
c) r = 9, d = 3.
Lời giải:
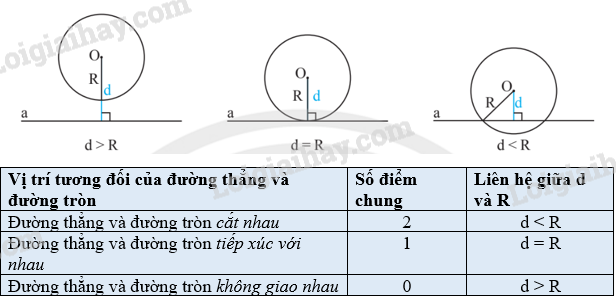
a) Vì 13 > 5 hay d > r nên a và (O; r) không giao nhau.
b) Vì 8 = 8 hay d = r nên a tiếp xúc với (O; r).
c) Vì 3 < 9 hay d < r nên a cắt (O; r) tại hai điểm.
Bài 4 trang 89 sách bài tập Toán 9 Tập 1: Cho góc vuông xOy có hai cạnh tiếp xúc với đường tròn (I; R) tại A, B. Cho biết chu vi của tứ giác OAIB bằng 20 cm. Tính R và độ dài AB.
Lời giải:
Ta có Ox và Oy tiếp xúc với (I; R) lần lượt tại A và B
Suy ra IA ⊥ Ox tại A, IB ⊥ Oy tại B và IA = IB = R.
Tứ giác OAIB có ba góc vuông và có hai cạnh kề bằng nhau (IA = IB) nên OAIB là hình vuông. Do đó IA = IB = OA = OB = R.
Khi đó, chu vi của hình vuông OAIB là 4R.
Theo bài, chu vi của tứ giác OAIB bằng 20 cm nên 4R = 20, suy ra R = 5 cm.
Xét ∆IAB vuông tại I, theo định lí Pythagore, ta có:
AB2 = IA2 + IB2 = 2R2 = 2.52 = 50.
Suy ra
Bài 5 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D. Cho biết Tính:
a) Số đo
b) Độ dài các đoạn thẳng AC, AB, AO.
(Làm tròn kết quả đến hàng đơn vị của mét.)
Lời giải:
a) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AO là tia phân giác của suy ra
Xét ∆OAC vuông tại C có
Suy ra hay
Xét ∆ODC cân tại O (do OC = OD), có
b) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AC = AB.
Xét ∆OAC vuông tại C ta có:
⦁
Do đó AC = AB ≈ 33 cm.
⦁
Suy ra
Bài 6 trang 89 sách bài tập Toán 9 Tập 1: Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm
a) Tính độ dài đường cao OH của tam giác AOB.
b) Chứng minh đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.
c) Tính độ dài các đoạn thẳng AH và BH.
Lời giải:
a) Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc nhau.
Áp dụng định lí Pythagore vào ∆AOB vuông tại O, ta có:
Ta có
Suy ra OA.OB = OH.AB
Do đó
b) Lần lượt vẽ các đường cao OK, OE, OF của tam giác BOC, COD, DOA.
Ta có bốn tam giác vuông AOB, AOD, COD, COB bằng nhau (c.g.c), suy ra bốn đường cao OH, OF, OE, OK cũng bằng nhau. Do khoảng cách từ O đến bốn cạnh của hình thoi đều bằng OH nên đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.
c) Xét tam giác OAB vuông tại O có:
Xét tam giác OAH vuông tại H có:
Do đó BH = AB – AH = 10 – 3,6 = 6,4 (cm).
Bài 7 trang 89 sách bài tập Toán 9 Tập 1: Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilômét? Biết rằng bán kính Trái Đất là khoảng 6 400 km. Làm tròn kết quả đến hàng phần trăm.
Lời giải:
Theo đề bài ta có hình vẽ trên. Trong đó điểm M biểu diễn vị trí của người ngồi trên trạm quan sát, điểm A biểu diễn vị trí của trạm quan sát, điểm T biểu diễn điểm xa nhất mà người đó nhìn thấy. Khi đó đoạn thẳng MT là tầm nhìn xa tối đa từ M.
Vì T là điểm nhìn xa tối đa nên MT là tiếp tuyến của đường tròn (đường tròn coi như là bề mặt Trái Đất). Đặt h = MA = 15 m = 0,015 km, R = OA = OT = 6 400 km.
Áp dụng định lí Pythagore cho tam giác OTM vuông tại T, ta có:
MT2 = OM2 – OT2 = (h + R)2 – R2 = h2 + 2Rh
Suy ra
Vậy tầm nhìn xa tối đa của người đó là khoảng 13,86 km.
Lý thuyết Tiếp tuyến của đường tròn
1. Vị trí tương đối của đường thẳng và đường tròn
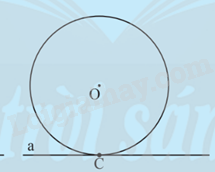
Đường thẳng a và đường tròn (O) có duy nhất một điểm chung C thì ta nói a tiếp xúc với (O) tại C, khi đó a là tiếp tuyến của đường tròn (O) tại C và C là tiếp điểm.
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Dấu hiệu nhận biết tiếp tuyến
|
Một đường thẳng là tiếp tuyến của đường tròn khi nó đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó. |
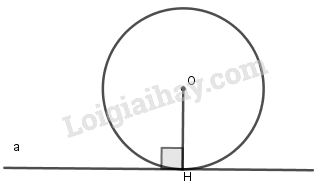
Tính chất của tiếp tuyến
|
- Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm. - Khoảng cách từ tâm của đường tròn đến tiếp tuyến luôn bằng bán kính của đường tròn đó. |
3. Tính chất của hai tiếp tuyến cắt nhau
Định lí
|
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: - Điểm đó cách đều hai tiếp điểm. - Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. - Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
|
Ví dụ: Cho đường tròn (O), B, C (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.
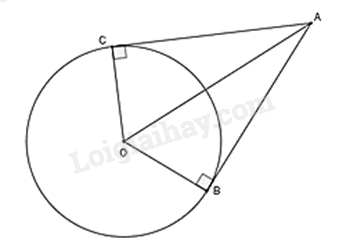
Khi đó:
- AB = AC
- Tia AO là tia phân giác của .
- Tia OA là tia phân giác của .
Xem thêm các bài giải SBT Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tiếp tuyến của đường tròn
Bài 3: Góc ở tâm, góc nội tiếp
Bài 4: Hình quạt tròn và hình vành khuyên