Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 2: Tiếp tuyến của đường tròn chi tiết sách Toán 9 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn

Khởi động trang 83 Toán 9 Tập 1: Hãy mô tả các vị trí của Mặt Trời so với đường chân trời ở các thời điểm Mặt Trời lặn khác nhau trong hình dưới đây.

Lời giải:

Sau bài học này, chúng ta giải quyết được câu hỏi trên như sau:

⦁ Hình a): Đường chân trời và Mặt Trời không giao nhau.

⦁ Hình b): Đường chân trời tiếp xúc với Mặt Trời.

⦁ Hình c): Đường chân trời cắt Mặt Trời.

1. Vị trí tương đối của đường thẳng và đường tròn

Khám phá 1 trang 83 Toán 9 Tập 1: Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau:

Lời giải:

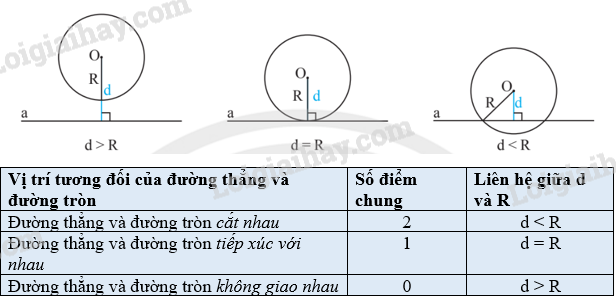
⦁ Hình 1a): đường thẳng a và đường tròn (O) không có điểm chung.

⦁ Hình 1b): đường thẳng a và đường tròn (O) có một điểm chung là điểm C.

⦁ Hình 1c): đường thẳng a và đường tròn (O) có hai điểm chung là điểm A và B.

Thực hành 1 trang 85 Toán 9 Tập 1: Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:

a) d = 4 cm;

b) d = 5 cm;

c) d = 6 cm.

Lời giải:

a)

Ta có d = 4 cm, R = 5 cm.

Vì d < R nên đường thẳng c cắt đường tròn (J; 5 cm) tại hai điểm.

b)

Ta có d = 5 cm, R = 5 cm.

Vì d = R nên đường thẳng c tiếp xúc với đường tròn (J; 5 cm) tại điểm K.

c)

Ta có d = 6 cm, R = 5 cm.

Vì d > R nên đường thẳng c và đường tròn (J; 5 cm) không giao nhau.

Vận dụng 1 trang 85 Toán 9 Tập 1: Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.

Lời giải:

Do sợi dây tiếp xúc với bánh xe nên khoảng cách từ trục bánh xe đến dây cáp bằng bán kính bánh xe.

Vậy khoảng cách từ trục bánh xe đến dây cáp là: $R=\frac{72}{2}=36\text{ (cm).}$

2. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Khám phá 2 trang 85 Toán 9 Tập 1: Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).

a) Giải thích tại sao ta có OA = R và OM > R.

b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.

Lời giải:

a) Vì điểm A nằm trên đường tròn (O; R) nên OA = R.

Ta có OA vuông góc với đường thẳng d tại A nên OA là khoảng cách từ điểm O đến đường thẳng d.

Do OA, OM lần lượt là đường vuông góc, đường xiên kẻ từ O đến đường thẳng d nên OA < OM.

Mà OA = R nên OM > R.

b) Ta có OA = R nên d tiếp xúc với đường tròn (O; R) tại A.

Mà khi đường thẳng d tiếp xúc với đường tròn (O; R) thì đường thẳng d và đường tròn (O; R) có duy nhất một điểm chung.

Vậy d và (O) không thể có điểm chung nào khác ngoài A.

Thực hành 2 trang 86 Toán 9 Tập 1: Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H.

Lời giải:

Ta có BC đi qua H thuộc đường tròn (A; AH) và BC ⊥ AH nên BC là tiếp tuyến của đường tròn (A; AH).

Vận dụng 2 trang 86 Toán 9 Tập 1: Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợi dây là tiếp tuyến của mỗi bánh xe, xác định các tiếp điểm.

Lời giải:

Tiếp điểm là giao điểm của mỗi nan hoa với dây cáp.

3. Tính chất của hai tiếp tuyến cắt nhau

Khám phá 3 trang 87 Toán 9 Tập 1: Cho đường tròn (O) và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).

a) Chứng minh hai tam giác ABO và ACO bằng nhau.

b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.

Lời giải:

a) Vì AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C nên AB ⊥ OB và AC ⊥ OC.

Xét ∆ABO và ∆ACO có:

$\widehat{ABO}=\widehat{ACO}=90°;$

OB = OC (cùng là bán kính của đường tròn (O));

OA là cạnh chung.

Do đó ∆ABO = ∆ACO (cạnh huyền – cạnh góc vuông).

b) Theo câu a, ∆ABO = ∆ACO, suy ra:

⦁ OB = OC; AB = AC (hai cạnh tương ứng);

⦁ $\widehat{ABO}=\widehat{ACO}=90°; \widehat{BAO}=\widehat{CAO};\widehat{BOA}=\widehat{COA}$ (các cặp góc tương ứng).

Thực hành 3 trang 87 Toán 9 Tập 1: Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết $\widehat{\text{EMF}}=60°.$

a) Tính số đo $\widehat{\text{EMI}}$ và $\widehat{\text{EIF}}.$

b) Tính độ dài MI.

Lời giải:

Vì ME, MF lần lượt là hai tiếp tuyến tại E, F của đường tròn (I) và cắt nhau tại M nên:

⦁ ME ⊥ IE tại E, MF ⊥ IF tại F hay $\widehat{IEM}=90°;\widehat{IFM}=90°;$

⦁ MI là tia phân giác của góc EMF. Do đó $\widehat{EMI}=\frac{1}{2}\widehat{EMF}=\frac{1}{2}\cdot 60°=30°.$

Xét tứ giác IEMF có: $\widehat{EIF}+\widehat{IEM}+\widehat{EMF}+\widehat{IFM}=360°$(tổng các góc của một tứ giác).

Suy ra $\widehat{EIF}=180°-\left(\widehat{IEM}+\widehat{EMF}+\widehat{IFM}\right)$

Hay $\widehat{EIF}=360°-\left(90°+60°+90°\right)=120°.$

b) Vì E thuộc đường tròn (I; 6 cm) nên IE = 6 cm.

Xét ∆IEM vuông tại E, ta có: $\sin \widehat{EMI}=\frac{IE}{MI}.$

Suy ra $MI=\frac{IE}{\sin \widehat{EMI}}=\frac{6}{\sin 30°}=12\text{ (cm).}$

Thực hành 4 trang 88 Toán 9 Tập 1: Tìm giá trị của x trong Hình 12.

Lời giải:

Ta có BA, BC là hai tiếp tuyến của đường tròn (D) cắt nhau tại B nên BA = BC hay 4x – 9 = 15, suy ra 4x = 24 nên x = 6.

Vận dụng 3 trang 88 Toán 9 Tập 1: Bánh đà của một động cơ được thiết kế có dạng là một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.

a) Tính độ dài của hai đoạn dây curoa MA và MB (kết quả làm tròn đến hàng phần mười).

b) Tính số đo $\widehat{\text{AMB}}$ tạo bởi hai tiếp tuyến AM, BM và số đo $\widehat{\text{AOB}}$ (kết quả làm tròn đến phút).

Lời giải:

a) Ta có MA, MB lần lượt là hai tiếp tuyến của đường tròn (O; 15 cm) tại A, B và cắt nhau tại M nên MA ⊥ OA, MB ⊥ OB và MA = MB.

Xét ∆OAM vuông tại A, theo định lí Pythagore ta có: OM² = OA² + MA².

Suy ra MA² = OM² – OA² = 35² – 15² = 1 000.

Do đó $MA=\sqrt{1000}\approx \mathrm{31,6}\text{ (cm).}$

Vậy MA = MB ≈ 31,6 cm.

b) Xét ∆OAM vuông tại A, ta có: $\sin \widehat{AMO}=\frac{OA}{OM}=\frac{15}{35}=\frac{3}{7}.$

Suy ra $\widehat{AMO}\approx 25°{23}^{\text{'}}.$

Vì MA, MB là hai tiếp tuyến của đường tròn (O; 15 cm) cắt nhau tại M nên MA là tia phân giác của góc AMB.

Do đó $\widehat{AMB}=2\widehat{AMO}\approx 2\cdot 25°{23}^{\text{'}}=50°{46}^{\text{'}}.$

Xét tứ giác OAMB có: $\widehat{OAM}+\widehat{AMB}+\widehat{OBM}+\widehat{AOB}=360°$(tổng các góc của một tứ giác).

Suy ra $\widehat{AOB}=360°-\left(\widehat{OAM}+\widehat{AMB}+\widehat{OBM}\right)$

Do đó $\widehat{AOB}\approx 360°-\left(90°+50°{46}^{\text{'}}+90°\right)=360°-230°{46}^{\text{'}}=129°{14}^{\text{'}}.$

Bài tập

Bài 1 trang 88 Toán 9 Tập 1: Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; $\widehat{\text{COB}}=130°.$ Tính số đo $\widehat{\text{CMB}}.$

Lời giải:

Vì MB, MC lần lượt là hai tiếp tuyến của đường tròn (O) tại B, C nên MB ⊥ OB, MC ⊥ OC hay $\widehat{MBO}=90°;\widehat{MCO}=90°.$

Xét tứ giác OBMC có: $\widehat{MCO}+\widehat{COB}+\widehat{MBO}+\widehat{CMB}=360°$ (tổng các góc của một tứ giác).

Suy ra $\widehat{CMB}=360°-\left(\widehat{MCO}+\widehat{COB}+\widehat{MBO}\right)$

Do đó $\widehat{CMB}=360°-\left(90°+130°+90°\right)=360°-310°=50°.$

Bài 2 trang 88 Toán 9 Tập 1: Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x.

Lời giải:

Ta có AB, AC là hai tiếp tuyến của đường tròn (O) cắt nhau tại A nên AB = AC hay 7x – 4 = 3x + 8.

Giải phương trình:

7x – 4 = 3x + 8

4x = 12

  x = 3.

Vậy x = 3.

Bài 3 trang 89 Toán 9 Tập 1: Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).

Lời giải:

Xét ∆ABC có:

⦁ AB² + BC² = 9² + 12² = 225;

⦁ AC² = 15² = 225.

Do đó AB² + BC² = AC²,

Theo định lí Pythagore đảo, ta có ∆ABC vuông tại B.

Suy ra AB ⊥ BC hay AB ⊥ OB.

Xét đường tròn (O) có AB ⊥ OB tại B thuộc đường tròn (O) nên AB là tiếp tuyến của đường tròn (O).

Bài 4 trang 89 Toán 9 Tập 1: Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm, BP = 3 cm, CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.

Lời giải:

Ta có:

⦁ AE, AM là hai tiếp tuyến của (O) cắt nhau tại A nên AE = AM = 6 cm (tính chất hai tiếp tuyến cắt nhau).

⦁ BM, BP là hai tiếp tuyến của (O) cắt nhau tại B nên BM = BP = 3 cm (tính chất hai tiếp tuyến cắt nhau).

⦁ CP, CE là hai tiếp tuyến của (O) cắt nhau tại C nên CP = CE = 8 cm (tính chất hai tiếp tuyến cắt nhau).

Chu vi tam giác ABC là:

AB + BC + CA = AM + BM + BP + CP + CE + AE

= 6 + 3 + 3 + 8 + 8 + 6 = 34 (cm).

Bài 5 trang 89 Toán 9 Tập 1: Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm của dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:

a) $\widehat{\text{ACB}}$ có số đo bằng 90°, từ đó suy ra độ dài của BC theo R;

b) OM là tia phân giác của $\widehat{\text{COA}};$

c) MC là tiếp tuyến của đường tròn (O; R).

Lời giải:

a) Vì A, B, C cùng nằm trên đường tròn (O; R) có đường kính AB nên $OA=OB=OC=\frac{1}{2}AB=R$ và AB = 2R.

Xét ∆ABC có CO là đường trung tuyến ứng với cạnh AB và $OC=\frac{1}{2}AB$ nên ∆ABC là tam giác vuông tại C. Do đó $\widehat{ACB}=90°.$

Xét ∆ABC vuông tại C, theo định lí Pythagore, ta có: AB² = BC² + AC².

Suy ra BC² = AB² – AC² = (2R)² – R² = 3R².

Do đó $BC=\sqrt{3R^2}=R\sqrt{3}.$

b) Xét ∆OAC có OA = OC nên ∆OAC là tam giác cân tại O.

∆OAC cân tại O có OI là đường trung tuyến ứng với cạnh đáy nên đồng thời là đường phân giác của tam giác.

Do đó OM là tia phân giác của $\widehat{\text{COA}}.$

c) Xét ∆OAM và ∆OCM có:

OA = OC = R;

$\widehat{AOM}=\widehat{COM}$ (do OM là tia phân giác của $\widehat{\text{COA}});$

OM là cạnh chung.

Do đó ∆OAM = ∆OCM (c.g.c).

Suy ra $\widehat{OAM}=\widehat{OCM}$(hai góc tương ứng).

Mà $\widehat{OAM}=90°$ nên $\widehat{OCM}=90°.$

Do đó MC ⊥ OC tại C, lại có C thuộc (O; R) nên MC là tiếp tuyến của đường tròn (O; R).

Bài 6 trang 89 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A, B là hai tiếp điểm) vuông góc với nhau tại M.

a) Tính độ dài của MA và MB.

b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài của CD.

Lời giải:

Vì MA, MB lần lượt là hai tiếp tuyến của đường tròn (O) tại A, B nên MA ⊥ OA và MB ⊥ OB hay $\widehat{OAM}=90°;\widehat{OBM}=90°.$

Xét tứ giác OAMB có: $\widehat{OAM}=90°;\widehat{OBM}=90°;\widehat{AMB}=90°$(do MA ⊥ MB).

Do đó tứ giác OAMB là hình chữ nhật.

Lại có OA = OB = 5 cm (do A, B nằm trên đường tròn (O; 5 cm)).

Suy ra hình chữ nhật OAMB là hình vuông, nên MA = MB = OA = OB = 5 cm.

b) Vì OAMB là hình vuông nên $\widehat{AOB}=90°$ và OM là tia phân giác của góc AOB.

Do đó $\widehat{AOM}=\widehat{BOM}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 90°=45°.$

Vì CD là tiếp tuyến của đường tròn (O) tại I nên CD ⊥ OI.

Xét ∆OCI vuông tại I, ta có: $CI=OI\cdot \tan \widehat{COI}=5\cdot \tan 45°=5\text{ (cm).}$

Xét ∆ODI vuông tại I, ta có: $DI=OI\cdot \tan \widehat{CDOI}=5\cdot \tan 45°=5\text{ (cm).}$

Vậy CD = CI + DI = 5 + 5 = 10 (cm).

Bài 7 trang 89 Toán 9 Tập 1: Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA và MB là hai tiếp tuyến (A, B là hai tiếp điểm) thỏa mãn $\widehat{\text{AMB}}=60°.$ Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.

Lời giải:

Vì MA và MB là hai tiếp tuyến tại A, B của đường tròn (O) cắt nhau tại M nên MA = MB (tính chất hai tiếp tuyến cắt nhau).

Do đó ∆MAB cân tại M, lại có $\widehat{\text{AMB}}=60°$ nên ∆MAB là tam giác đều.

Suy ra MA = MB = AB.

Chu vi ∆MAB là: MA + MB + AB = 3AB.

Theo bài, chu vi tam giác MAB là 18 cm nên 3AB = 18, do đó AB = 6 (cm).

Vậy AB = 6 cm.

Bài 8 trang 89 Toán 9 Tập 1: Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.

a) Tính bán kính r của đường tròn (O).

b) Tính chiều dài cạnh OA của tam giác ABO.

Lời giải:

a) Vì AB là tiếp tuyến của đường tròn (O) tại B nên AB ⊥ OB tại B.

Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có: OA² = OB² + AB²

Suy ra (OC + CA)² = OB² + AB²

Do đó (r + 2)² = r² + 4². (*)

Giải phương trình (*):

(r + 2)² = r² + 4²

r² + 4r + 4 = r² + 16

4r = 12

r = 3.

Vậy bán kính của đường tròn (O) là r = 3.

b) Ta có OA = OC + CA = r + 2 = 3 + 2 = 5 (cm).

Vậy OA = 5 cm.

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 1. Đường tròn

Bài 2. Tiếp tuyến của đường tròn

Bài 3. Góc ở tâm, góc nội tiếp

Bài 4. Hình quạt tròn và hình vành khuyên

Bài tập cuối chương 5

Hoạt động 1. Làm giác kế đo góc nâng đơn giản

Lý thuyết Tiếp tuyến của đường tròn

1. Vị trí tương đối của đường thẳng và đường tròn

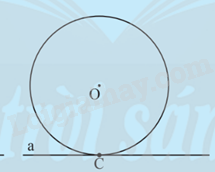
Đường thẳng a và đường tròn (O) có duy nhất một điểm chung C thì ta nói a tiếp xúc với (O) tại C, khi đó a là tiếp tuyến của đường tròn (O) tại C và C là tiếp điểm.

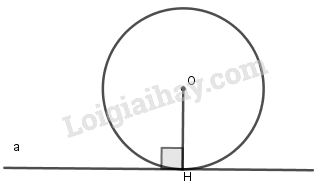
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Dấu hiệu nhận biết tiếp tuyến

Tính chất của tiếp tuyến

3. Tính chất của hai tiếp tuyến cắt nhau

Định lí

Ví dụ: Cho đường tròn (O), B, C $\in$ (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.

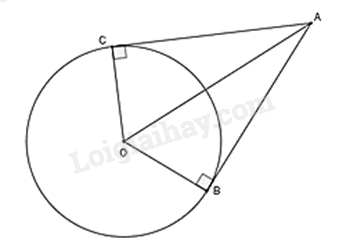
Khi đó:

- AB = AC

- Tia AO là tia phân giác của $\widehat{BAC}$.

- Tia OA là tia phân giác của $\widehat{BOC}$.