Với giải Luyện tập 3 trang 120 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
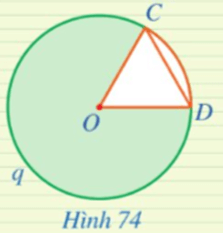
Luyện tập 3 trang 120 Toán 9 Tập 1: Cho hình quạt COD giới hạn bởi hai bán kính OC, OD và cung CqD sao cho OC = CD (Hình 74). Hãy tìm số đo cung CqD ứng với hình quạt đó.
Lời giải:
Xét ∆OCD có OC = OD = CD nên ∆OCD là tam giác đều, do đó
Vì góc COD là góc ở tâm chắn cung nhỏ CD nên
Do đó
Lý thuyết Diện tích hình quạt tròn
Chú ý:
- Hình tròn tâm O bán kính R bao gồm đường tròn (O;R) và tất cả các điểm nằm trong đường tròn đó.
- Diện tích của hình tròn bán kính R là .
Khái niệm hình quạt tròn
|
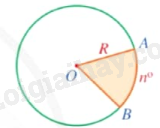
Hình quạt tròn (hay còn gọi tắt là hình quạt) là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó.
|
Diện tích hình quạt tròn
|
Diện tích hình quạt tròn bán kính R ứng với cung :
|
Nhận xét: Gọi là độ dài của cung tròn có số đo thì diện tích hình quạt tròn bán kính R, cung tròn có số đo là:
.
Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là cm, bán kính là R = 5cm là:
Xem thêm lời giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
Khởi động trang 118 Toán 9 Tập 1: Hình 65 mô tả một chiếc quạt giấy........
Hoạt động 1 trang 118 Toán 9 Tập 1: Lấy một vòng tròn không dãn có dạng hình tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b........
Luyện tập 1 trang 118 Toán 9 Tập 1: Tính chu vi của đường tròn bán kính 5 cm (theo đơn vị centimet và làm tròn kết quả đến hàng phần mười)........
Hoạt động 2 trang 119 Toán 9 Tập 1: a) Đánh dấu hai điểm A, B trên một vòng dây không dãn có dạng đường tròn (Hình 67a), cắt cung AB của vòng dây và kéo thẳng cung đó để nhận được sợi dây như ở Hình 67b.......
Luyện tập 2 trang 119 Toán 9 Tập 1: Một con lắc di chuyển từ vị trí A đến vị trí B (Hình 69). Tính độ dài quãng đường AB mà con lắc đó đã di chuyển, biết rằng sợi dây OA có độ dài bằng l và tia OA tạo với phương thẳng đứng góc α.......
Hoạt động 3 trang 119 Toán 9 Tập 1: Vẽ đường tròn (O; 2 cm) và các điểm A, B thỏa mãn OA < 2 cm, OB = 2 cm. Nêu nhận xét về vị trí các điểm A, B so với đường tròn (O; 2 cm)........
Hoạt động 4 trang 120 Toán 9 Tập 1: Quan sát Hình 71, hãy cho biết phần hình tròn (O) tô màu xanh được giới hạn bởi hai bán kính và cung nào?........
Luyện tập 3 trang 120 Toán 9 Tập 1: Cho hình quạt COD giới hạn bởi hai bán kính OC, OD và cung CqD sao cho OC = CD (Hình 74). Hãy tìm số đo cung CqD ứng với hình quạt đó........
Hoạt động 5 trang 120 Toán 9 Tập 1: Ta coi mỗi hình tròn bán kính R là một hình quạt có số đo 360°. Tính diện tích hình quạt tròn tâm O, bán kính R, biết số đo cung ứng với hình quạt tròn đó là:.......
Luyện tập 4 trang 121 Toán 9 Tập 1: Hình quạt tô màu đỏ ở Hình 65 có bán kính bằng 2 dm và góc ở tâm bằng 150°........
Hoạt động 6 trang 122 Toán 9 Tập 1: a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm?......
Luyện tập 5 trang 122 Toán 9 Tập 1: Tính diện tích của hình vành khuyên đó giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 2,5 cm; 2 cm.......
Bài 1 trang 122 Toán 9 Tập 1: Quan sát các hình 83, 84, 85, 86.......
Bài 2 trang 123 Toán 9 Tập 1: Hình87 mô tả mặt cắt của chiếc đèn led có dạng hình vành khuyên màu trắng với bán kính các đường tròn lần lượt là 15 cm, 18 cm, 21 cm, 24 cm. Tính diện tích hai hình vành khuyên đó......
Bài 3 trang 123 Toán 9 Tập 1: Hình 88 mô tả mặt cắt của một khung gỗ có dạng ghép của năm hình: hai nửa hình tròn đường kính 2 cm; hai hình chữ nhật kích thước 2 cm × 8 cm (Hình 88b); một phần tư hình vành khuyên giới hạn bởi hai đường tròn cùng tâm có bán kính lần lượt là 4 cm và 6 cm. Tính diện tích của mặt cắt của khung gỗ đó.......
Bài 4 trang 123 Toán 9 Tập 1: Khi đóng đáy thuyền cho những con thuyền vượt biển, người Vikings sử dụng hai loại nêm: nêm góc và nêm cong (lần lượt tô màu xanh, màu đỏ trong Hình 89). Mặt cắt ABCD của nêm góc có dạng hai tam giác vuông OAE, ODE bằng nhau với cạnh huyền chung và bỏ đi hình quạt tròn OBC (Hình 90), được làm từ những thân cây mọc thẳng. Mặt cắt MNPQ của nêm cong có dạng một phần của hình vành khuyên (Hình 91), được làm từ những thân cây cong. Kích thước của nêm cong được cho như ở Hình 91.......
Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
§4. Góc ở tâm. Góc nội tiếp
§5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
Bài tập cuối chương 5
§1. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
§2. Tần số. Tần số tương đối
§3. Tần số ghép nhóm. Tần số tương đối ghép nhóm
