Với giải Hoạt động 2 trang 112 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 4: Góc ở tâm. Góc nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp

Hoạt động 2 trang 112 Toán 9 Tập 1: Quan sát góc ở tâm AOB (khác góc bẹt) ở Hình 48, cho biết trong hai phần đường tròn được tô màu xanh và màu đỏ, phần nào nằm bên trong, phần nào nằm bên ngoài góc AOB.

Lời giải:

Phần đường tròn được tô màu xanh nằm bên trong góc AOB.

Phần đường tròn được tô màu đỏ nằm bên ngoài góc AOB.

Lý thuyết Cung, số đo cung

Cung

Phần đường tròn nối liền hai điểm A, B trên đường tròn được gọi là một cung (hay cung tròn) AB, kí hiệu là $\stackrel{⌢}{AB}$.

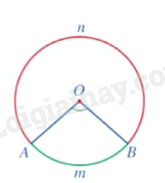
Góc ở tâm $\widehat{AOB}$ chắn cung AnB hay cung AnB bị chắn bởi góc ở tâm $\widehat{AOB}$.

$\stackrel{⌢}{AnB}$ là cung nhỏ và $\stackrel{⌢}{AmB}$ là cung lớn.

Số đo cung

Quy ước: Khi hai mút của cung trùng nhau, ta có “cung không” với số đo $0^0$ và cung cả đường tròn có số đo ${360}^0$.

Nhận xét: Góc ở tâm chắn một cung mà cung đó là nửa đường tròn thì có số đo bằng ${180}^0$.

Nếu điểm C là một điểm nằm trên cung AB thì sđ$\stackrel{⌢}{ACB}$ = sđ$\stackrel{⌢}{AC}$ + sđ$\stackrel{⌢}{CB}$.

Chú ý:

- Khác với so sánh hai góc, ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bằng nhau. Cụ thể:

+ Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau;

+ Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Hai cung AB và CD bằng nhau được kí hiệu là $\stackrel{⌢}{AB}=\stackrel{⌢}{CD}$.

Cung EG nhỏ hơn cung HK được kí hiệu là $\stackrel{⌢}{EG}<\stackrel{⌢}{HK}$. Trong trường hợp này, ta cũng nói cung HK lớn hơn cung EG và kí hiệu là $\stackrel{⌢}{HK}>\stackrel{⌢}{EG}$.

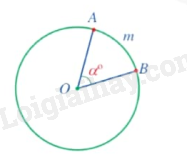
- Cho điểm $A$ thuộc đường tròn $(O)$ và số thực $\alpha$ với $0<\alpha <360$. Sử dụng thược thẳng và thước đo độ, ta vẽ điểm $B$ thuộc đường tròn $(O)$ như sau:

+ Nếu $0<\alpha \le 180$ thì ta vẽ theo chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng ${\alpha }^0$. Khi đó sđ$\stackrel{⌢}{AmB}={\alpha }^0$

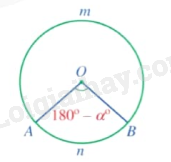
+ Nếu $180<\alpha \le 360$ thì ta vẽ theo ngược chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng ${\alpha }^0-{180}^0$. Khi đó sđ$\stackrel{⌢}{AnB}={\alpha }^0$.