Với giải Bài 4 trang 71 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

Bài 4 trang 71 Toán 9 Tập 1: Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762 m, $\widehat{A}=6°,\widehat{B}=4°.$

a) Tính chiều cao h của con dốc.

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.

Lời giải:

a) Đặt AH = x (m) (0 < x < 762).

Suy ra BH = 762 – x (m).

Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:

 h = x . tan 6° và h = (762 – x) . tan 4°.

Suy ra x . tan 6° = (762 – x) . tan 4°

x . tan 6° = 762 . tan 4° – x . tan 4°

x . tan 6° + x . tan 4° = 762 . tan 4°

x . (tan 6° + tan 4°) = 762 . tan 4°

$x=\frac{762.\tan 4°}{\tan 6°+\tan 4°}$.

Do đó $h=\frac{762.\tan 4°}{\tan 6°+\tan 4°}\cdot \tan 6°\approx 32\left(m\right)$ .

Vậy chiều cao h của con dốc khoảng 32 m.

b) Xét tam giác AHC vuông tại H có $\widehat{A}=6°$  nên h = AC . sin A.

Suy ra $AC=\frac{h}{\sin A}=\frac{32}{\sin 6°}\approx 306,1\text{\hspace{0.17em}\hspace{0.17em}(m)}=0,3061\text{\hspace{0.17em}\hspace{0.17em}(km)}$ .

Xét tam giác BHC vuông tại H có $\widehat{B}=4°$  nên h = BC . sin B.

Suy ra $BC=\frac{h}{\sin B}=\frac{32}{\sin 4°}\approx 458,7\text{\hspace{0.17em}\hspace{0.17em}(m)}=0,4587\text{\hspace{0.17em}\hspace{0.17em}(km)}$ .

Thời gian An đi từ nhà đến trường là:

$\frac{0,3061}{4}+\frac{0,4587}{19}\approx 0,1$ (giờ) = 6 phút.

Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà và đến trường vào lúc:

6 giờ + 6 phút = 6 giờ 6 phút.

Vậy bạn An đến trường lúc 6 giờ 6 phút.

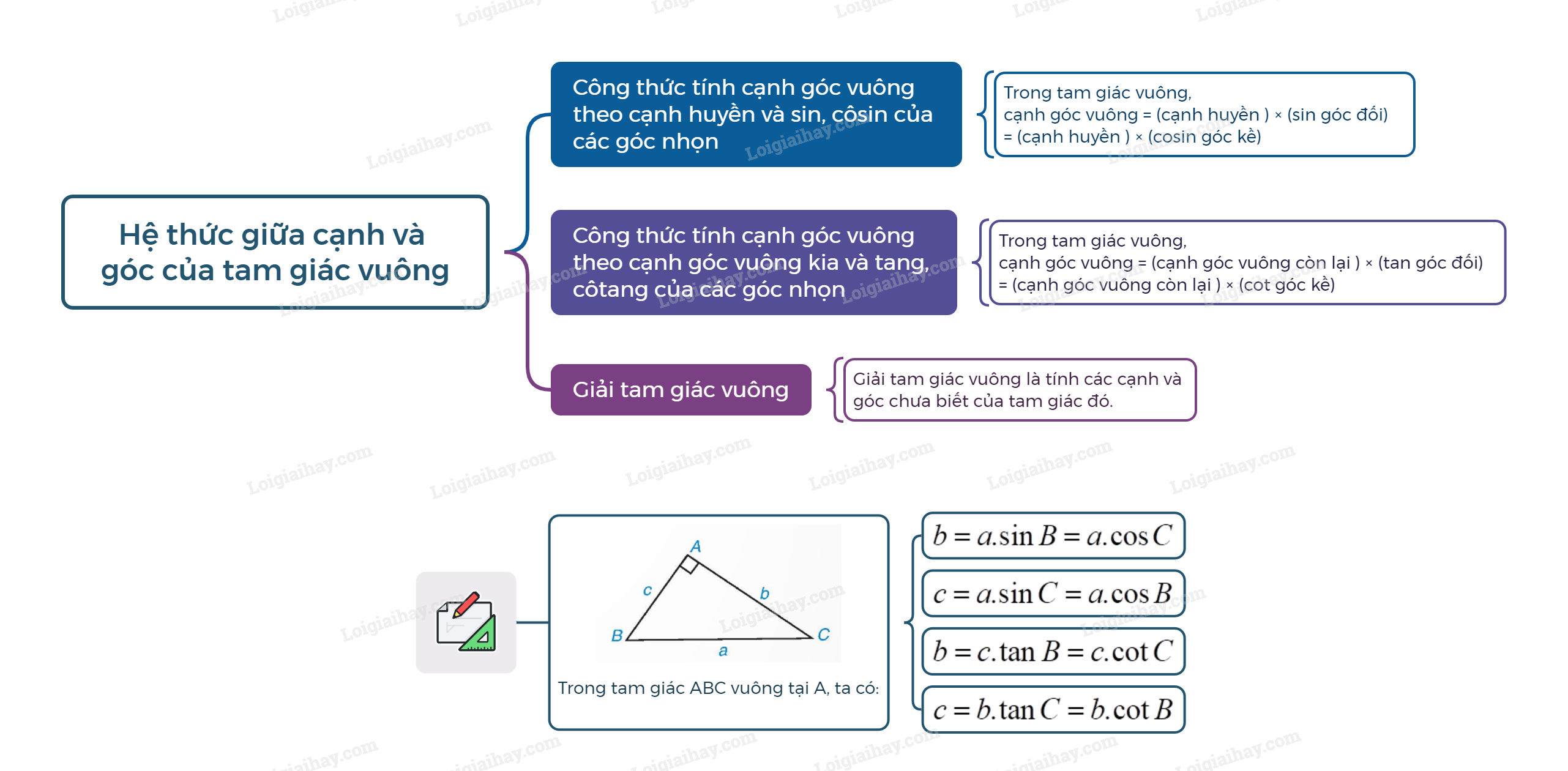
Sơ đồ tư duy Hệ thức giữa cạnh và góc của tam giác vuông