Với giải Thực hành 2 trang 68 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông
Thực hành 2 trang 68 Toán 9 Tập 1: Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).
Lời giải:
a) Hình 3a: Xét tam giác ABC vuông tại A, , ta có:
x = AB = AC . cot B = 9 . cot 32° ≈ 14,40.
Vậy x ≈ 14,40.
b) Hình 3b: Xét tam giác DEF vuông tại F, , ta có:
x = DF = EF . tan E = 5 . tan 48° ≈ 5,55.
Vậy x ≈ 5,55.
Lý Thuyết Hệ thức giữa cạnh và góc của tam giác vuông
Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn
|
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Cạnh góc vuông = (cạnh huyền ) × (sin góc đối) = (cạnh huyền ) × (cosin góc kề) |
Ví dụ 1:
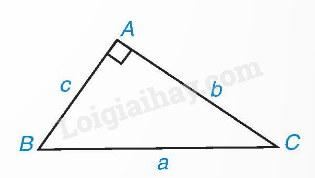
Trong tam giác ABC vuông tại A, ta có:
Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn
|
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề. Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối) = (cạnh góc vuông còn lại ) × (cot góc kề) |
Ví dụ 2:
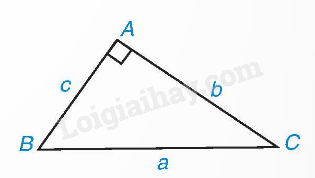
Trong tam giác ABC vuông tại A, ta có:
Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Khám phá 1 trang 67 Toán 9 Tập 1: Cho tam giác ABC vuông tại A (Hình 1).......
Vận dụng 2 trang 70 Toán 9 Tập 1: Trong Hình 9, cho OH = 4 m, Tính chiều cao AB của dây......
Bài 2 trang 71 Toán 9 Tập 1: Cho tam giác ABC có BC = 20 cm, ......
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 1. Tỉ số lượng giác của góc nhọn
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
