Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông chi tiết sách Toán 9 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

Khởi động trang 67 Toán 9 Tập 1: Làm thế nào để tính chiều cao BC khi biết khoảng cách AB và góc A trong hình bên?

Lời giải:

Để tính được chiều cao BC thì ta dựa vào tỉ số lượng giác.

Xét tam giác ABC vuông tại B có AB = 64 m và $\widehat{A}=49°$ .

Ta có $\tan A=\frac{BC}{AB}$  hay $\tan 49°=\frac{BC}{64}$ .

Suy ra BC = 64 . tan 49° ≈ 73,62 (m).

Vậy để tính chiều cao BC khi biết khoảng cách AB và góc A ta dựa vào tỉ số lượng giác.

1. Hệ thức giữa cạnh và góc của tam giác vuông

Khám phá 1 trang 67 Toán 9 Tập 1: Cho tam giác ABC vuông tại A (Hình 1).

a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao lại có các đẳng thức: b = a . sin B; c = a . cos B.

b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao lại có các đẳng thức: b = c . tan B; c = b . cot B.

Lời giải:

Xét tam giác vuông ABC, ta có:

a) $\sin B=\frac{AC}{BC}=\frac{b}{a}$  suy ra b = a . sin B;

$\cos B=\frac{AB}{BC}=\frac{c}{a}$ suy ra c = a . cos B.

b) $\tan B=\frac{AC}{AB}=\frac{b}{c}$ suy ra b = c . tan B;

$\cot B=\frac{AB}{AC}=\frac{c}{b}$ suy ra c = b . cot B.

Thực hành 1 trang 68 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20 cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm):

a) $\widehat{B}=36°;$

b) $\widehat{C}=41°.$

Lời giải:

a)

Xét tam giác ABC vuông tại A, $\widehat{B}=36°$ , ta có:

• AB = BC . cos B = 20 . cos 36° ≈ 16,18 (cm).

• AC = BC . sin B = 20 . sin 36° ≈ 11,76 (cm).

Vậy AB ≈ 16,18 cm; AC ≈ 11,76 cm.

b)

Xét tam giác ABC vuông tại A, $\widehat{C}=41°$ , ta có:

• AB = BC . sin C = 20 . sin 41° ≈ 13,12 (cm).

• AC = BC . cos C = 20 . cos 41° ≈ 15,09 (cm).

Vậy AB ≈ 13,12 cm; AC ≈ 15,09 cm.

Thực hành 2 trang 68 Toán 9 Tập 1: Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).

Lời giải:

a) Hình 3a: Xét tam giác ABC vuông tại A,$\widehat{B}=32°$ , ta có:

x = AB = AC . cot B = 9 . cot 32° ≈ 14,40.

Vậy x ≈ 14,40.

b) Hình 3b: Xét tam giác DEF vuông tại F, $\widehat{E}=48°$ , ta có:

x = DF = EF . tan E = 5 . tan 48° ≈ 5,55.

Vậy x ≈ 5,55.

Vận dụng 1 trang 68 Toán 9 Tập 1: Một cần cẩu đang nâng một khối gõ trên sông. Biết tay cẩu AB có chiều dài là 16 m và nghiêng một góc 42° so với phương nằm ngang (Hình 4). Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần trăm).

Lời giải:

Xét tam giác ABC vuông tại C có $\widehat{A}=48°$ , ta có:

BC = AB . sin 42° = 16 . sin 42° ≈ 10,71 (m).

Vậy chiều dài BC của đoạn dây cáp khoảng 10,71 m.

2. Giải tam giác vuông

Khám phá 2 trang 69 Toán 9 Tập 1: Cho tam giác ABC (Hình 5). Em hãy cho biết trong các trường hợp nào sau đây, ta có thể tính được tất cả các cạnh và các góc của tam giác. Giải thích cách tính.

Lời giải:

Ta xét các trường hợp sau:

– Trường hợp 1 khi biết độ dài hai cạnh của tam giác vuông thì ta sẽ tìm được cạnh còn lại (áp dụng định lí Pythagore) và các góc (áp dụng tỉ số lượng giác).

– Trường hợp 2 khi biết được số đo hai góc thì ta tính được số đo của góc còn lại (dựa vào định lí tổng ba góc trong một tam giác) nhưng chưa đủ dữ kiện để tính độ dài các cạnh của tam giác.

– Trường hợp 3 khi biết một cạnh và một góc của tam giác vuông ta sẽ tìm được cạnh còn lại và các góc (áp dụng tỉ số lượng giác).

Vậy trong các trường hợp đã cho, trường hợp 1 và trường hợp 3 ta có thể tính được tất cả các cạnh và các góc của tam giác.

Vận dụng 2 trang 70 Toán 9 Tập 1: Trong Hình 9, cho OH = 4 m, $\widehat{AOH}=42°,\widehat{HOB}=28°.$ Tính chiều cao AB của dây.

Lời giải:

Xét tam giác OHA vuông tại H, ta có

AH = OH . tan 42° = 4 . tan 42° ≈ 3,6 (m).

Xét tam giác OHB vuông tại H, ta có

HB = OH . tan 28° = 4 . tan 28° ≈ 2,1 (m).

Chiều cao AB của cây là: AH + HB ≈ 3,6 + 2,1 = 5,7 (m).

Vậy chiều cao AB của cây khoảng 5,7 m.

Bài tập

Bài 1 trang 71 Toán 9 Tập 1: Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và $\widehat{BAC}=68°$ (Hình 10).

Lời giải:

Xét tam giác ABC vuông tại B có $\widehat{BAC}=68°$ , ta có:

• $AB=AC.\cos \widehat{BAC}=16.\cos 68°=6\text{\hspace{0.17em}\hspace{0.17em}(cm)}$

• $BC=AC.\sin \widehat{BAC}=16.\sin 68°=14,8\text{\hspace{0.17em}\hspace{0.17em}(cm)}$

Vì ABCD là hình chữ nhật nên ta có AB = CD = 6 cm và BC = AD = 14,8 cm.

Vậy độ dài các cạnh của hình chữ nhật ABCD là AB = 6 cm và BC = 14,8 cm, CD = 6 cm, AD = 14,8 cm.

Bài 2 trang 71 Toán 9 Tập 1: Cho tam giác ABC có BC = 20 cm, $\widehat{ABC}=22°,\widehat{ACB}=30°.$

a) Tính khoảng cách từ điểm B đến đường thẳng AC.

b) Tính các cạnh và các góc còn lại của tam giác ABC.

c) Tính khoảng cách từ điểm A đến đường thẳng BC.

Lời giải:

a) Gọi BH là đường cao hạ từ B xuống AC.

Khi đó, BH là khoảng cách từ điểm B đến đường thẳng AC.

Xét tam giác BHC có $\widehat{ACH}=30°$ , ta có:

BH = BC . sin 30° = 20 . sin 30° = 10 (cm).

Vậy khoảng cách từ điểm B đến đường thẳng AC là 10 cm.

b) Xét tam giác ABC, ta có: $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$ .

Suy ra $\widehat{BAC}=180°-\widehat{ABC}-\widehat{ACB}=180°-30°-22°=128°.$

Ta có $\widehat{BAH}=180°-\widehat{BAC}=180°-128°=52°.$

Xét tam giác ABH vuông tại H có $\widehat{BAH}=52°$  nên

•  $AB.\sin \widehat{BAH}=10$ suy ra $AB=\frac{BH}{\sin \widehat{BAH}}=\frac{10}{\sin 52°}\approx 12,7\text{\hspace{0.17em}\hspace{0.17em}(cm)}$ .

• $AH.\tan \widehat{BAH}=10$  suy ra $AH=\frac{BH}{\tan \widehat{BAH}}=\frac{10}{\tan 52°}\approx 7,8\text{\hspace{0.17em}\hspace{0.17em}(cm)}$ .

Áp dụng định lý Pythagore vào tam giác BHC, ta có: BC² = CH ² + BH²

Suy ra $CH=\sqrt{B{C}^2–B{H}^2}=\sqrt{{20}^2–{10}^2}=10\sqrt{3}\text{\hspace{0.17em}\hspace{0.17em}(cm)}$ .

Do đó $AC=CH-AH\approx 10\sqrt{3}-7,8\approx 9,5\text{\hspace{0.17em}\hspace{0.17em}(cm)}$ .

Vậy độ dài các cạnh và các góc còn lại của tam giác ABC là $\widehat{BAC}=128°$ , AB ≈ 7,9 cm, AC ≈ 9,5 cm.

c) Gọi AK là đường cao hạ từ A xuống BC.

Khi đó, AK là khoảng cách từ điểm A đến đường thẳng BC.

Xét tam giác ACK có $\widehat{ACK}=30°$  và AC ≈ 9,5 cm nên ta có:

$AK=AC.\sin \widehat{ACK}\approx 9,5.\sin 30°\approx 4,8\text{\hspace{0.17em}\hspace{0.17em}(cm)}$

Vậy khoảng cách từ điểm A đến đường thẳng BC khoảng 4,8 cm.

Bài 3 trang 71 Toán 9 Tập 1: Một người đẩy một vật lên hết một con dốc nghiêng một góc 35° (Hình 11).

Lời giải:

Nhìn vào hình ta có tam giác vuông ABC như hình sau:

Xét tam giác ABC vuông tại B có $\widehat{ACB}=35°$  nên

$AB=BC.\sin \widehat{ACB}=4.\sin 35°\approx 2,3\text{\hspace{0.17em}\hspace{0.17em}(m)}$

Vậy độ cao của vật so với mặt đất khoảng 2,3 m.

Bài 4 trang 71 Toán 9 Tập 1: Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762 m, $\widehat{A}=6°,\widehat{B}=4°.$

a) Tính chiều cao h của con dốc.

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.

Lời giải:

a) Đặt AH = x (m) (0 < x < 762).

Suy ra BH = 762 – x (m).

Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:

 h = x . tan 6° và h = (762 – x) . tan 4°.

Suy ra x . tan 6° = (762 – x) . tan 4°

x . tan 6° = 762 . tan 4° – x . tan 4°

x . tan 6° + x . tan 4° = 762 . tan 4°

x . (tan 6° + tan 4°) = 762 . tan 4°

$x=\frac{762.\tan 4°}{\tan 6°+\tan 4°}$.

Do đó $h=\frac{762.\tan 4°}{\tan 6°+\tan 4°}\cdot \tan 6°\approx 32\left(m\right)$ .

Vậy chiều cao h của con dốc khoảng 32 m.

b) Xét tam giác AHC vuông tại H có $\widehat{A}=6°$  nên h = AC . sin A.

Suy ra $AC=\frac{h}{\sin A}=\frac{32}{\sin 6°}\approx 306,1\text{\hspace{0.17em}\hspace{0.17em}(m)}=0,3061\text{\hspace{0.17em}\hspace{0.17em}(km)}$ .

Xét tam giác BHC vuông tại H có $\widehat{B}=4°$  nên h = BC . sin B.

Suy ra $BC=\frac{h}{\sin B}=\frac{32}{\sin 4°}\approx 458,7\text{\hspace{0.17em}\hspace{0.17em}(m)}=0,4587\text{\hspace{0.17em}\hspace{0.17em}(km)}$ .

Thời gian An đi từ nhà đến trường là:

$\frac{0,3061}{4}+\frac{0,4587}{19}\approx 0,1$ (giờ) = 6 phút.

Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà và đến trường vào lúc:

6 giờ + 6 phút = 6 giờ 6 phút.

Vậy bạn An đến trường lúc 6 giờ 6 phút.

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 1. Tỉ số lượng giác của góc nhọn 

Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông

Bài tập cuối chương 4

Bài 1. Đường tròn

Bài 2. Tiếp tuyến của đường tròn

Bài 3. Góc ở tâm, góc nội tiếp

Lý thuyết Hệ thức giữa cạnh và góc của tam giác vuông

1. Hệ thức giữa cạnh và góc của tam giác vuông

Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn

Ví dụ 1:

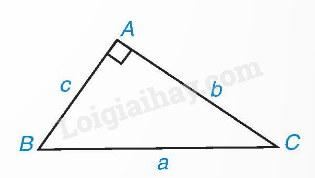
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=a.\sin B=a.\cos C;\\ c=a.\sin C=a.\cos B.\end{array}$

Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn

Ví dụ 2:

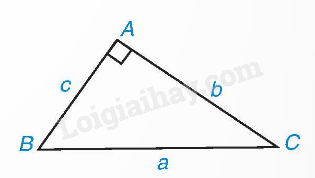
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=c.\tan B=c.\cot C;\\ c=b.\tan C=b.\cot B.\end{array}$

2. Giải tam giác vuông

Giải tam giác vuông là tính các cạnh và góc chưa biết của tam giác đó.