Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên chi tiết sách Toán 9 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Mở đầu trang 91 Toán 9 Tập 1: Số người trên một địa bàn đã được tiêm mũi 4 phòng dịch Covid-19 đạt 40% trong tổng số các đối tượng cần được tiêm. Để hoàn thành một biểu đồ hình quạt tròn, Trang cần vẽ hình quạt tròn biểu thị số liệu 40%. Em có thể giúp bạn Trang được không?

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Để vẽ đường tròn bán kính bất kì, ta cần lấy một bán kính làm mốc.

Ta có 40% của 360° là: 360° . 40% = 144°.

Từ bán kính làm gốc ta đo góc 144°, nối từ tâm đến điểm đạt tại 144°, ta được phần biểu đồ cần vẽ ứng với 40%.

Tô màu phần vừa biểu diễn ta được biểu đồ hình quạt tròn như sau:

1. Độ dài của cung tròn

HĐ1 trang 91 Toán 9 Tập 1: Biết rằng trên một đường tròn, hai cung bằng nhau thì có cùng độ dài và độ dài của cung tỉ lệ với số đo của nó. Từ đó hay lập công thức tính độ dài cung n° của đường tròn bán kính R bằng cách thực hiện các bước sau:

a) Từ (1), tính độ dài của cung 1°.

b) Tính độ dài l của cung n°.

Lời giải:

a) Đường tròn là cung có số đo bằng 360° và có độ dài bằng 2πR.

Suy ra độ dài của cung 1° là: $\frac{2\pi R}{360}=\frac{\pi R}{180}.$

b) Độ dài của cung n° là: l$=n\cdot \frac{\pi R}{180}.$

Luyện tập 1 trang 92 Toán 9 Tập 1: Tính độ dài cung 40° của đường tròn bán kính 9 cm.

Lời giải:

Độ dài cung 40° là: l$=\frac{40}{180}.\pi .9=2\pi \text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Vậy độ dài cung 40° của đường tròn bán kính 9 cm là 2π (cm).

Vận dụng 1 trang 92 Toán 9 Tập 1: Bánh xe (khi bơm căng) của một chiếc xe đạp có đường kính 650 mm. Biết rằng khi giò đĩa quay một vòng thì bánh xe đạp quay được khoảng 3,3 vòng (H.5.14). Hỏi chiếc xe đạp di chuyển được quãng đường dài bao nhiêu mét sau khi người đi xe đạp 10 vòng liên tục?

Hướng dẫn: Khi bánh xe quay 3,3 vòng thì mỗi điểm trên bánh xe di chuyển được một độ dài bằng 3,3 lần chu vi đường tròn.

Lời giải:

Chu vi của bánh xe là: C = 650π (mm).

Khi người đi xe đạp 10 vòng thì xe đạp di chuyển được quãng đường bằng:

C = 650π . 3,3 . 10 = 21 450π ≈ 6 738,72 (mm) = 6,738 (m).

Vậy chiếc xe đạp di chuyển được quãng đường dài khoảng 6,738 mét sau khi người đi xe đạp 10 vòng liên tục.

2. Hình quạt tròn và hình vành khuyên

Câu hỏi trang 93 Toán 9 Tập 1: Em hãy tìm một số hình ảnh của hình quạt tròn và hình vành khuyên trong thực tế.

Lời giải:

Một số hình ảnh của quạt tròn trong thực tế: chiếc quạt gấp, bánh pizza,…

+ Chiếc quạt gấp:

+ Bánh pizza:

Một số hình ảnh của hình vành khuyên: lốp xe, viền của chiếc đồng hồ, viền của loa,…

+ Lốp xe:

+ Viền của chiếc đồng hồ:

+ Viền của loa:

HĐ2 trang 93 Toán 9 Tập 1: Biết rằng hai hình quạt tròn ứng với hai cung bằng nhau trên một đường tròn thì có diện tích bằng nhau và diện tích quạt tròn tỉ lệ với số đo của cung tương ứng với nó. Hãy thiết lập công thức tính diện tích hình quạt tròn bán kính R với cung n° bằng cách thực hiện từng bước sau:

a) Tính diện tích hình quạt tròn ứng với cung 1°.

b) Tính diện tích hình quạt tròn ứng với cung n°.

Lời giải:

a) Đường tròn là cung có số đo bằng 360° và có độ dài bằng πR².

Suy ra diện tích hình quạt tròn ứng với cung 1° là $\frac{\pi R^2}{360}.$

b) Diện tích hình quạt tròn ứng với của cung n° là $\frac{n}{360}\cdot \pi R^2$

HĐ3 trang 93 Toán 9 Tập 1: Thiết lập công thức tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r).

Lời giải:

Diện tích hình tròn bán kính R là πR².

Diện tích hình tròn bán kính r là: πr².

Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r) là: πR² − πr² = π(R² − r²).

Thực hành trang 94 Toán 9 Tập 1: Trở lại tình huống mở đầu. Hãy vẽ (tô màu) hình quạt tròn theo hướng dẫn sau:

− Vẽ đường tròn tâm O (với bán kính tùy chọn).

− Hình quạt tròn cần vẽ ứng với cung có số đo bằng 40% của 360°. Tính số đo của cung cần vẽ.

− Vẽ góc ở tâm có số đo tìm được và tô màu hình quạt tròn tương ứng.

Lời giải:

− Vẽ đường tròn tâm O (với bán kính tùy chọn).

− Hình quạt tròn cần vẽ ứng với cung có số đo bằng 40% của 360°.

Ta có 40% của 360° là: 360° . 40% = 144°.

− Vẽ góc ở tâm có số đo 144°: Từ bán kính làm gốc ta đo góc 144°, nối từ tâm đến điểm đạt tại 144°, ta được phần biểu đồ cần vẽ ứng với 40%.

Tô màu phần vừa biểu diễn ta được biểu đồ hình quạt tròn như sau:

Luyện tập 2 trang 94 Toán 9 Tập 1: Tính diện tích của hình quạt tròn đã vẽ trong Thực hành trên nếu bán kính của nó bằng 4 cm.

Lời giải:

Hình quạt tròn ứng với cung có số đo là:

360° . 40% = 144°.

Diện tích hình quạt tròn là:

$S=\frac{n}{360}\cdot \pi R^2=\frac{144}{360}\cdot \pi .4^2=6,4\pi \left({\text{cm}}^{\text{2}}\right)$.

Vậy diện tích của hình quạt tròn là 6,4π (cm²).

Vận dụng 2 trang 94 Toán 9 Tập 1: Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính là 5 cm, 10 cm, 15 cm, 20 cm và 30 cm (H.5.17).

Giả thiết rằng người ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba), biết rằng xác xuất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.

Lời giải:

Diện tích của vòng 8 là: π(15² − 10²) = 125π (cm²).

Diện tích hình tròn lớn nhất là: π . 30² = 900π (cm²).

Xác suất ném trúng vòng 8 là: $\frac{125\pi }{900\pi }=\frac{5}{36}.$

Vậy xác suất ném trúng vòng 8 là $\frac{5}{36}.$

Bài tập

Bài 5.9 trang 94 Toán 9 Tập 1: Cho đường tròn (O; 4 cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng 70°.

a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau.

b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười).

Lời giải:

a) Xét ΔOAB và ΔOAC có:

Cạnh OA chung

OA = OC = R

AB = AC (do ΔABC cân tại A).

Do đó ΔOAB = ΔOAC (c.c.c).

Suy ra $\widehat{AOB}=\widehat{AOC}$ (hai góc tương ứng).

Khi đó $sđ\stackrel{⏜}{AB}=sđ\stackrel{⏜}{AC}$  nên $\stackrel{⏜}{AB}=\stackrel{⏜}{AC}$ .

Vậy hai cung nhỏ AB và AC bằng nhau.

b) Độ dài cung BC là: $\frac{70}{180}.\pi .4=\frac{14}{9}\pi \approx 4,9\text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Ta có: $\widehat{AOB}+\widehat{AOC}+\widehat{BOC}=360°$

$2.\widehat{AOB}+70°=360°$

$2.\widehat{AOB}=290°$

$\widehat{AOB}=145°$

Độ dài cung AB và cung AC là: $\frac{145}{180}.\pi .4=\frac{29}{9}\pi \approx 10,1\text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Vậy độ dài cung BC khoảng 4,9 cm và độ dài cung AB và cung AC khoảng 10,1 cm.

Bài 5.10 trang 95 Toán 9 Tập 1: Tính diện tích của hình quạt tròn bán kính 4 cm, ứng với cung 36°.

Lời giải:

Diện tích của hình quạt tròn bán kính 4 cm, ứng với cung 36° là:

$\frac{36}{360}.\pi .4^2=1,6\pi \left({\text{cm}}^{\text{2}}\right)$.

Vậy diện tích của hình quạt tròn bán kính 4 cm, ứng với cung 36° là 1,6π cm².

Bài 5.11 trang 95 Toán 9 Tập 1: Tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 5 cm và 4 cm.

Lời giải:

Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 5 cm và 4 cm là:

π(5² − 4²) = 9π (cm²).

Vậy diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 5 cm và 4 cm là 9π cm².

Bài 5.12 trang 95 Toán 9 Tập 1: Có hai chiếc bánh pizza hình tròn (H.5.18). Chiếc bánh thứ nhất có đường kính 16 cm được cắt thành 6 miếng đều nhau có dạng hình quạt tròn. Chiếc bánh thứ hai có đường kính 18 cm được cắt thành 8 miếng đều nhau có dạng hình quạt tròn. Hãy so sánh diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất và thứ hai.

Lời giải:

Diện tích bề mặt của mỗi miếng bánh cắt ra từ chiếc bánh thứ nhất là

$\frac{\pi .{16}^2}{6}=\frac{128}{3}\pi \left({\text{cm}}^{\text{2}}\right)$

Diện tích bề mặt của mỗi miếng bánh cắt ra từ chiếc bánh thứ hai là:

$\frac{\pi .{18}^2}{8}=\frac{81}{2}\pi \left({\text{cm}}^{\text{2}}\right)$

Vì $\frac{128}{3}\pi >\frac{81}{2}\pi$  nên miếng bánh cắt ra từ chiếc bánh thứ nhất lớn hơn chiếc bánh thứ hai.

Vậy diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất lớn hơn chiếc bánh thứ hai.

Bài 5.13 trang 95 Toán 9 Tập 1: Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn bán kính 2,2 dm như hình 5.19. Tính diện tích phần giấy của chiếc quạt, biết rằng khi gấp lại, phần giấy có chiều dài khoảng 1,6 dm (làm tròn kết quả đến hàng trăm của dm²).

Lời giải:

Diện tích phần giấy của chiếc quạt là:

π(2,2² − 1,6²) = 2,28π (dm²).

Vậy diện tích phần giấy của chiếc quạt là 2,28π (dm²).

Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Bài 14. Cung và dây của một đường tròn

Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Luyện tập chung trang 96

Bài 16. Vị trí tương đối của đường thẳng và đường tròn

Bài 17. Vị trí tương đối của hai đường tròn

Luyện tập chung trang 108

Lý thuyết Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

1. Độ dài của cung tròn

Công thức tính độ dài đường tròn (chu vi đường tròn)

Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:

$C=\pi d=2\pi R$

Công thức tính độ dài cung tròn

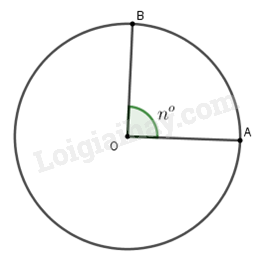
Công thức tính độ dài l của cung tròn $n^o$ trên đường tròn (O;R) là:

Tỉ số giữa độ dài cung $n^o$ và độ dài đường tròn (cùng bán kính) đúng bằng $\frac{n}{360}$.

$\frac{l}{C}=\frac{\frac{n}{180}\pi R}{2\pi R}=\frac{n}{360}$

Ví dụ:

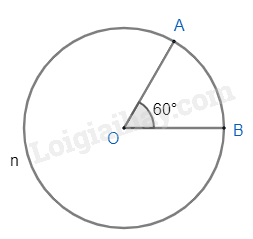
Đường tròn (O; 2cm), $\widehat{AOB}={60}^0$.

- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.

Do đó sđ$\stackrel{⌢}{AB}=\widehat{AOB}={60}^0$

Độ dài $l_1$ của cung AB là:

$l_1=\frac{n}{180}\pi R=\frac{60}{180}\pi .2=\frac{2\pi }{3}\approx 2,1\left(cm\right)$

Cung lớn AnB có số đo là:

sđ$\stackrel{⌢}{AmN}={360}^o-{60}^0={300}^0$.

Độ dài $l_2$ của cung AnB là:

$l_2=\frac{300}{180}\pi .2=\frac{10}{3}\pi \approx 10,5\left(cm\right)$

2. Hình quạt tròn và hình vành khuyên

Khái niệm hình quạt tròn

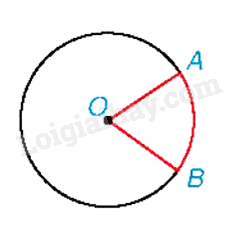
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó.

Khái niệm hình vành khuyên

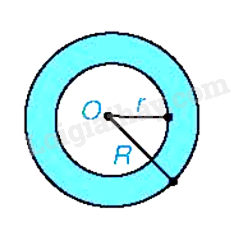
Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là hai đường tròn đồng tâm)

Diện tích hình quạt tròn

Diện tích hình vành khuyên

Tỉ số giữa diện tích hình quạt tròn ứng với cung $n^0$ và diện tích hình tròn (cùng bán kính) đúng bằng $\frac{n}{360}$ và bằng tỉ số giữa độ dài cung $n^0$ và độ dài đường tròn.

Ví dụ:

1. Diện tích hình quạt tròn có độ dài tương ứng với nó là $l=4\pi$cm, bán kính là R = 5cm là:

$S_q=\frac{l.R}{2}=\frac{4\pi .5}{2}=10\pi \left(c{m}^2\right)$

2. Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:

$S_v=\pi \left(5^2-3^2\right)=16\pi \left(m^2\right)$