Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn chi tiết sách Toán 9 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn

Mở đầu trang 99 Toán 9 Tập 1: Người ta gieo một đồng xu hình tròn bán kính 1 cm lên một tờ giấy trải phẳng. Trên tờ giấy đó có vẽ những đường thẳng song song cách đều, tức là những đường thẳng song song mà khoảng cách giữa hai đường thẳng bất kì nằm cạnh nhau luôn bằng nhau. Nếu khoảng cách ấy luôn bằng 2 cm thì có thể xảy ra những trường hợp nào sau đây, vì sao?

a) Đồng xu đè lên một đường thẳng (đồng xu che khuất một phần của đường thẳng).

b) Đồng xu không đè lên đường thẳng nào?

c) Đồng xu đè lên nhiều hơn một đường thẳng.

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Đặt tên các đường thẳng a, b, c, d như hình vẽ dưới đây:

Đường kính của đồng xu là: 2 . 1 = 2 (cm).

a) Đường kính của đồng xu là 2 cm và bằng khoảng cách giữa hai đường thẳng song song.

Do đó, đồng xu đè có thể lên một đường thẳng (đồng xu che khuất một phần của đường thẳng).

b) Đồng xu không đè lên đường thẳng a và đường thẳng d.

c) Đồng xu chỉ cắt tối đa một đường thẳng (tức là đè lên một đường thẳng) hoặc đồng xu nằm giữa hai đường thẳng (hai đường thẳng tiếp xúc với đường tròn viền ngoài của đồng xu) hay đồng xu không đè lên đường thẳng nào.

Do đó, không xảy ra trường hợp đồng xu đè lên nhiều hơn một đường thẳng.

1. Vị trí tương đối của đường thẳng và đường tròn

HĐ1 trang 99 Toán 9 Tập 1: Cho đường thẳng a và điểm O. Gọi H là chân đường vuông góc hạ từ O xuống a, và A là một điểm thuộc tia OH. Trong mỗi trường hợp sau đây, hãy vẽ đường tròn (O; OA) và cho biết đường thẳng a và đường tròn (O; OA) có bao nhiêu điểm chung?

Lời giải:

a)

Đường thẳng a và đường tròn có 2 điểm chung.

b)

Đường thẳng a và đường tròn có 1 điểm chung.

c)

Đường thẳng a và đường tròn không có điểm chung.

Luyện tập 1 trang 100 Toán 9 Tập 1: Cho đường thẳng a và điểm O cách a một khoảng bằng 4 cm. Không vẽ hình, hãy dự đoán xem mỗi đường tròn sau cắt, tiếp xúc hay không cắt đường thẳng a. Tại sao?

a) (O; 3 cm).

b) (O; 5 cm).

c) (O; 4 cm).

Lời giải:

a) Vì R = 3 cm < 4 cm nên đường tròn (O; 3 cm) không cắt đường thẳng a.

b) Vì R = 5 cm > 4 cm nên đường tròn (O; 5 cm) cắt đường thẳng a.

c) Vì R = 4 cm nên đường tròn (O; 4 cm) tiếp xúc với đường thẳng a.

2. Dấu hiệu nhận biết tiếp tuyến của đường tròn

HĐ2 trang 100 Toán 9 Tập 1: Cho đoạn thẳng OH và đường thẳng a vuông góc với OH tại H.

a) Xác định khoảng cách từ O đến đường thẳng a.

b) Nếu vẽ đường thẳng (O; OH) thì đường tròn này và đường thẳng a có vị trí tương đối như thế nào?

Lời giải:

a) Khoảng cách từ O đến đường thẳng a bằng OH.

b) Nếu vẽ đường thẳng (O; OH) thì đường tròn (O; OH) tiếp xúc với đường thẳng a.

Luyện tập 2 trang 101 Toán 9 Tập 1: Cho một hình vuông có độ dài mỗi cạnh bằng 6 cm và hai đường chéo cắt nhau tại I. Chứng minh rằng đường tròn (I; 3 cm) tiếp xúc với cả bốn cạnh của hình vuông.

Lời giải:

Gọi ABCD là hình vuông có độ dài mỗi cạnh bằng 6 cm; H là chân đường vuông góc kẻ từ I đến BC.

Khi đó H cũng là trung điểm của BC.

Do ABCD là hình vuông nên AC và BD vuông góc.

Tam giác IBC vuông tại I có trung tuyến IH

Suy ra:$IH=HB=HC=\frac{BC}{2}=3\text{\hspace{0.17em}\hspace{0.17em}(cm)}$.

Suy ra đường tròn (I; 3 cm) tiếp xúc với cạnh BC.

Tương tự ta cũng chứng minh được (I; 3 cm) tiếp xúc với 3 cạnh còn lại.

Vậy (I; 3 cm) tiếp xúc với cả bốn cạnh của hình vuông.

Thực hành trang 101 Toán 9 Tập 1: Cho đường thẳng a và điểm M không thuộc a. Hãy vẽ đường tròn tâm M tiếp xúc với a.

Lời giải:

− Từ điểm M kẻ MH ⊥ a (H ∈ a).

− Vẽ đường tròn tâm M, bán kính MH.

− Từ đó ta vẽ được đường tròn tâm M tiếp xúc với a.

Vận dụng trang 101 Toán 9 Tập 1: Trở lại tình huống mở đầu. Ở đây, ta hiểu đồng xu nằm đè lên một đường thẳng khi đường tròn (hình ảnh của đồng xu) và đường thẳng ấy cắt nhau.

Bằng cách xét vị trí của tâm đồng xu trong một dải nằm giữa hai đường thẳng song song cạnh nhau (cách đều hoặc không cách đều hai đường thẳng đó), hãy chứng minh rằng chỉ xảy ra các trường hợp a và b, không thể xảy ra trường hợp c.

Lời giải:

Đặt tên các đường thẳng a, b, c, d như hình vẽ dưới đây:

Đường kính của đồng xu là: 2 . 1 = 2 (cm).

a) Đường kính của đồng xu là 2 cm và bằng khoảng cách giữa hai đường thẳng song song.

Do đó, đồng xu đè có thể lên một đường thẳng (đồng xu che khuất một phần của đường thẳng).

b) Đồng xu không đè lên đường thẳng a và đường thẳng d.

c) Đồng xu chỉ cắt tối đa một đường thẳng (tức là đè lên một đường thẳng) hoặc đồng xu nằm giữa hai đường thẳng (hai đường thẳng tiếp xúc với đường tròn viền ngoài của đồng xu) hay đồng xu không đè lên đường thẳng nào.

Do đó, không xảy ra trường hợp đồng xu đè lên nhiều hơn một đường thẳng.

Vậy chỉ xảy ra các trường hợp a và b, không thể xảy ra trường hợp c.

3. Hai tiếp tuyến cắt nhau của một đường tròn

HĐ3 trang 101 Toán 9 Tập 1: Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:

− Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B;

− Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).

Lời giải:

• Tam giác OAM có O'A = O'O = O'M (cùng là bán kính của đường tròn (O')) nên tam giác OAM vuông tại A.

Suy ra: AM ⊥ OA tại A hay AM là tiếp tuyến của đường tròn (O').

• Tam giác OBM có O'B = O'O = O'M (cùng là bán kính của đường tròn (O')) nên tam giác OAM vuông tại B.

Suy ra: MB ⊥ OB tại B hay MB là tiếp tuyến của đường tròn (O').

HĐ4 trang 102 Toán 9 Tập 1: (Dựa vào hình vẽ có được sau HĐ3). Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:

a) MA = MB;

b) MO là tia phân giác của góc AMB;

c) OM là tia phân giác của góc AOB.

Lời giải:

a) Xét hai tam giác vuông OAM và OBM có:

OA = OB; OM chung

Do đó ΔOAM = ΔOBM (cạnh huyền – cạnh góc vuông).

Suy ra AM = BM (hai cạnh tương ứng).

b) Vì ΔOAM = ΔOBM (câu a) nên $\widehat{OAM}=\widehat{OBM}$  (hai góc tương ứng).

Suy ra OM là tia phân giác của góc AMB.

c) Vì ΔOAM = ΔOBM (câu a) nên $\widehat{AOM}=\widehat{BOM}$  (hai góc tương ứng).

Suy ra Om là tia phân giác của góc AOB.

Thử thách nhỏ trang 103 Toán 9 Tập 1: Cho góc xMy và điểm A thuộc tia Mx. Hãy vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy sao cho A là một trong hai tiếp điểm.

Lời giải:

− Vẽ góc xMy, lấy điểm A trên Mx.

− Vẽ tia Oz là tia phân giác của góc xMy.

− Từ A kẻ At ⊥ Mx, tia At cắt tia Mz tại điểm O.

− Vẽ đường tròn (O; OA), ta được đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy sao cho A là một trong hai tiếp điểm.

Bài tập

Bài 5.20 trang 103 Toán 9 Tập 1: Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a?

Lời giải:

• Vì a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm nên đường thẳng a tiếp xúc với hình tròn bán kính 6 cm, hay hình tròn bán kính 6 cm đè lên đường thẳng a.

• Vì 4 cm < 6 cm nên đường thẳng a và hình tròn bán kính 4 cm không cắt nhau, hay hình tròn bán kính 4 cm không đè lên trường thẳng a.

• Vì 7 cm > 6 cm; 8 cm > 6 cm nên đường thẳng a và hình tròn bán kính 4 cm cắt nhau, hay hình tròn bán kính 7 cm và 8 cm đè lên đường thẳng a.

Vậy hình tròn bán kính 4 cm không đè lên trường thẳng a, hình tròn bán kính 6 cm, 7 cm và 8 cm đè lên đường thẳng a.

Bài 5.21 trang 103 Toán 9 Tập 1: Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).

Lời giải:

Ta có đường thẳng AO là trục đối xứng của đường tròn.

Nên B là điểm đối xứng của C qua AO.

Gọi H là giao điểm của AO và BC.

Khi đó ta có: AH ⊥ BC mà d // BC nên AH ⊥  d.

Vậy d là một tiếp tuyến của đường tròn.

Bài 5.22 trang 103 Toán 9 Tập 1: Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).

Lời giải:

Xét ΔOAM và ΔOBM có:

OM chung

$\widehat{AOM}=\widehat{BOM}$ (do OM là tia phân giác của góc $\widehat{AOB}$ )

OA = OB

Do đó ΔOAM = ΔOBM (c.g.c).

Suy ra AM = BM (hai cạnh tương ứng).

Và $\widehat{OAM}=\widehat{OBM}=90°$  (hai góc tương ứng) hay OB ⊥ MB.

Do đó OA là tiếp tuyến của đường tròn (M; MA).

Vậy OA và OB là hai tiếp tuyến cắt nhau của (O).

Bài 5.23 trang 103 Toán 9 Tập 1: Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.

a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.

b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.

Lời giải:

a)

Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA.

Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB.

Chu vi tam giác SEF là:

C_SEF = SE + SF + EF = SE + SF + EM + MF

= SE + EA + SF + BF = SA + SB.

Vậy chu vi của tam giác SEF bằng SA + SB.

b)

Vì SA và SB là hai tiếp tuyến cắt nhau tại S nên SO là phân giác của .

Suy ra $\widehat{OSA}=\widehat{OSB}$  hay $\widehat{MSE}=\widehat{MSF}$ .

Xét ΔSME và ΔSMF có:

$\widehat{SME}=\widehat{SMF}=90°$

SM chung

$\widehat{MSE}=\widehat{MSF}$

Do đó ΔSME = ΔSMF (g.c.g)

Suy ra SE = SF (hai cạnh tương ứng).

Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 96

Bài 16. Vị trí tương đối của đường thẳng và đường tròn

Bài 17. Vị trí tương đối của hai đường tròn

Luyện tập chung trang 108

Bài tập cuối chương 5

Pha chế dung dịch theo nồng độ yêu cầu

Lý thuyết Vị trí tương đối của đường thẳng và đường tròn

1. Vị trí tương đối của đường thẳng và đường tròn

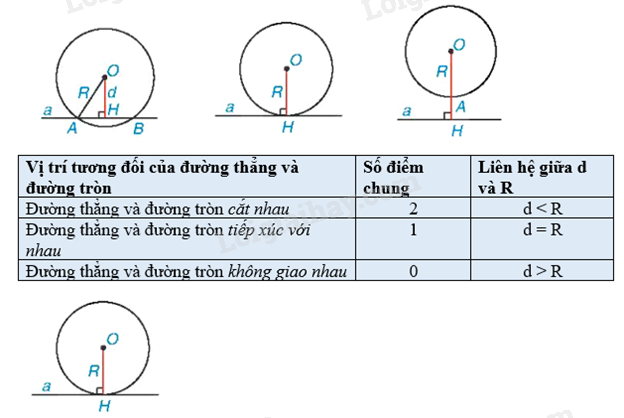
Điểm chung H của đường thẳng và đường tròn tiếp xúc với nhau goi là tiếp điểm. Khi đó đường thẳng a còn gọi là tiếp tuyến của đường tròn (O) tại H.

Đường thẳng a tiếp xúc với đường tròn (O) tại H thì $OH\mathrm{\perp }a$.

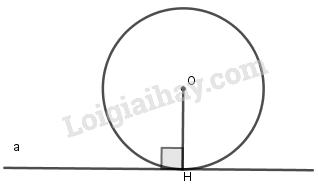
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Dấu hiệu nhận biết tiếp tuyến

3. Hai tiếp tuyến cắt nhau của một đường tròn

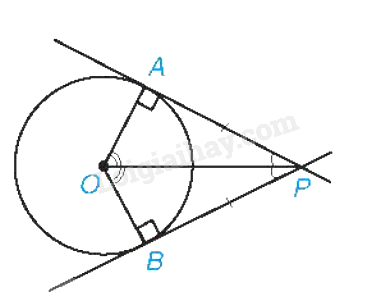
Tính chất của hai tiếp tuyến cắt nhau

Ví dụ: Cho đường tròn (O), B, C $\in$ (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.

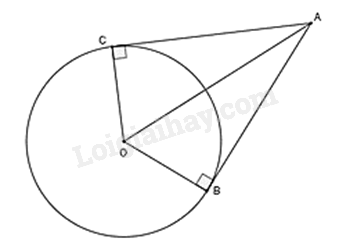
Khi đó:

- AB = AC

- Tia AO là tia phân giác của $\widehat{BAC}$.

- Tia OA là tia phân giác của $\widehat{BOC}$.