Với giải sách bài tập Toán 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Bài 5.11 trang 62 sách bài tập Toán 9 Tập 1: Cho hình thoi ABCD có $\widehat{A}$ = 75° và AB = 6 cm. Vẽ đường tròn (D), bán kính 6 cm.

a) Chứng minh rằng $A,C\in \left(D\right)$

b) Tính độ dài cung nhỏ AC và diện tích hình quạt tròn ứng với cung nhỏ AC.

Lời giải:

a) Vì ABCD là hình thoi nên DA = DC = 6 cm.

Mà đường tròn (D) có bán kính bằng 6 cm nên A và C nằm trên đường tròn D.

Vậy $A,C\in \left(D\right)$. (đpcm)

b) Vì ABCD là hình thoi nên $\widehat{BAD}+\widehat{ADC}=180°$

Suy ra $\widehat{ADC}=180°-\widehat{BAD}=180°-75°=105°$

Độ dài cung nhỏ AC là: $\frac{n}{180}\cdot \pi R=\frac{105}{180}\pi \cdot 6=\frac{7}{2}\pi$(cm).

Diện tích hình quạt tương ứng với cung nhỏ AC là:

$S=\frac{n}{360}\cdot \pi R^2=\frac{105}{360}\pi \cdot 6^2=\frac{21}{2}\pi$ (cm²).

Vậy độ dài cung nhỏ AC là $\frac{7}{2}\pi$cm và diện tích hình quạt tương ứng với cung nhỏ AC là $\frac{21}{2}\pi$cm².

Bài 5.12 trang 62 sách bài tập Toán 9 Tập 1 Độ dài của một cung tròn bằng $\frac{2}{5}$ chu vi của hình tròn có cùng bán kính. Tính diện tích của hình quạt tròn ứng với cung tròn đó, biết diện tích của hình tròn là S = 20 cm².

Lời giải:

Theo đề bài ta có: $\frac{l}{C}=\frac{2}{5}$, suy ra $\frac{n}{360}=\frac{2}{5}$

Diện tích hình quạt ứng với cung tròn đó là:

$\frac{n}{360}\cdot \pi R^2=\frac{n}{360}\cdot S=\frac{2}{5}\cdot 20=8$ (cm²)

Vậy diện tích của hình quạt tròn ứng với cung tròn đó là 8 cm².

Bài 5.13 trang 62 sách bài tập Toán 9 Tập 1 Trên bờ của một cái ao cá hình tròn, người ta dựng ba cái chòi câu cá tại các điểm A, B và C. Biết rằng tam giác ABC cân tại B và có AB = BC = 10 m, $\widehat{ABC}$ = 120° (H.5.5).

a) Tính bán kính của ao cá.

b) Tính độ dài quãng đường (men theo bờ ao) từ chòi A đến chòi B và chòi C (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Gọi O là tâm cái ao. Do đó OA = OC, suy ra O nằm trên đường trung trực của AC.

Mà tam giác ABC cân tại B nên đường trung trực của AC đồng thời là đường phân giác của góc ABC, do đó:

$\widehat{ABO}=\frac{\widehat{ABC}}{2}=\frac{120°}{2}=60°$

Do OA = OB (bán kính đường tròn (O)) mà $\widehat{ABO}=60°$ nên tam giác OAB là tam giác đều, suy ra OA = AB = 10 cm.

Vậy bán kính ao cá là 10 cm.

b) Độ dài quãng đường từ A đến B là độ dài cung nhỏ AB và có giá trị bằng:

$\frac{n}{180}\cdot \pi R=\frac{60}{180}\pi \cdot 10=\frac{10}{3}\pi \approx \mathrm{10,8}$ (m)

Ta thấy AB = BC = AO = OC = 10 cm nên ABCO là hình thoi.

Suy ra BO là đường phân giác của góc AOC.

Do đó độ dài cung nhỏ AB bằng độ dài cung nhỏ BC.

Suy ra quãng đường từ A đến C bằng 2 lần độ dài cung nhỏ AB và bằng:

$2\cdot \frac{10}{3}\pi =\frac{20}{3}\pi \approx \mathrm{20,9}$ (m).

Vậy quãng đường từ A đến B dài xấp xỉ 10,8 m và quãng đường từ A đến C dài xấp xỉ 20,9 m.

Bài 5.14 trang 62 sách bài tập Toán 9 Tập 1: Giả định rằng Trái Đất quay xung quanh Mặt Trời theo một quỹ đạo tròn có bán kính khoảng 150 triệu kilômét và phải hết đúng một năm (365 ngày) để hoàn thành một vòng quay. Hãy tính quãng đường Trái Đất đi được trong một ngày (làm tròn đến hàng nghìn theo đơn vị kilômét).

Lời giải:

Quãng đường trái đất đi được trong một ngày bằng $\frac{1}{365}$ quãng đường trái đất đi được trong 1 năm.

Quãng đường trái đất đi được trong 1 năm là:

$2\pi R=2\pi \cdot 150000000=300000000\pi$ (km)

Vậy quãng đường trái đất đi được trong 1 ngày là:

$\frac{1}{365}\cdot 300000000\pi \approx 2582000$ (km).

Bài 5.15 trang 62 sách bài tập Toán 9 Tập 1: Năm học vừa qua, kết quả xếp loại học lực cuối năm học sinh của một huyện được biểu thị trong biểu đổ hình quạt tròn như hình bên: Hãy tìm số đo của các cung tròn tương ứng với mỗi hình quạt biểu thị các số liệu cho trên hình.

Lời giải:

Cung tròn ứng với hình quạt biểu thị tỉ lệ học sinh được xếp loại tốt có số đo bằng:

35% . 360° = 126°.

Cung tròn ứng với hình quạt biểu thị tỉ lệ học sinh được xếp loại khá có số đo bằng:

40% . 360° = 144°.

Cung tròn ứng với hình quạt biểu thị tỉ lệ học sinh được xếp loại trung bình có số đo bằng: 25% . 360° = 90°.

Vậy số đo các cung tròn tương ứng với các hình quạt biểu thị tỉ lệ học sinh được xếp loại tốt, khá, trung bình lần lượt bằng 126°, 144°, 90°.

Bài 5.16 trang 62 sách bài tập Toán 9 Tập 1: Một chiếc bánh pizza hình tròn được chia thành 8 miếng như nhau bởi 4 nhát cắt qua tâm (H.5.6).

a) Mỗi miếng bánh có dạng một hình quạt tròn ứng với cung bao nhiêu độ?

b) Người ta chọn một chiếc hộp có đáy là hình vuông để đặt lọt chiếc bánh vào trong đó (mà vẫn giữ nguyên hình tròn). Hỏi mỗi cạnh đáy của chiếc hộp đó tối thiểu phải dài bao nhiêu centimét (làm tròn đến hàng đơn vị), biết rằng Hình 5.6 diện tích bề mặt mỗi miếng bánh bằng 60 cm²?

Lời giải:

a) Số đo cung tròn ứng với hình quạt tương ứng với miếng pizza là:

$\frac{360°}{8}=45°$

b) Độ dài cạnh chiếc hộp hình vuông tối thiểu phải bằng độ dài đường kính của chiếc bánh pizza.

Diện tích chiếc bánh pizza là: 8 . 60 = 480 (cm²)

Gọi R là bán kính chiếc bánh, ta có: $\pi R^2=480$

Suy ra $R=\sqrt{\frac{480}{\pi }}\approx \mathrm{12,4}$(cm)

Đường kính chiếc bánh là: 12,4 . 2 = 24,8 (cm)

Vậy độ dài cạnh chiếc hộp hình vuông tối thiểu phải bằng 25 cm.

Lý thuyết Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

1. Độ dài của cung tròn

Công thức tính độ dài đường tròn (chu vi đường tròn)

Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:

$C=\pi d=2\pi R$

Công thức tính độ dài cung tròn

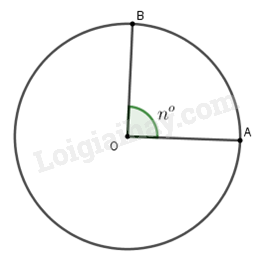
Công thức tính độ dài l của cung tròn $n^o$ trên đường tròn (O;R) là:

Tỉ số giữa độ dài cung $n^o$ và độ dài đường tròn (cùng bán kính) đúng bằng $\frac{n}{360}$.

$\frac{l}{C}=\frac{\frac{n}{180}\pi R}{2\pi R}=\frac{n}{360}$

Ví dụ:

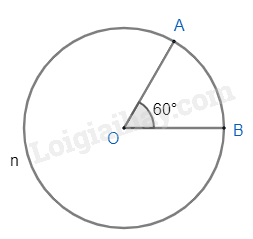
Đường tròn (O; 2cm), $\widehat{AOB}={60}^0$.

- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.

Do đó sđ$\stackrel{⌢}{AB}=\widehat{AOB}={60}^0$

Độ dài $l_1$ của cung AB là:

$l_1=\frac{n}{180}\pi R=\frac{60}{180}\pi .2=\frac{2\pi }{3}\approx 2,1\left(cm\right)$

Cung lớn AnB có số đo là:

sđ$\stackrel{⌢}{AmN}={360}^o-{60}^0={300}^0$.

Độ dài $l_2$ của cung AnB là:

$l_2=\frac{300}{180}\pi .2=\frac{10}{3}\pi \approx 10,5\left(cm\right)$

2. Hình quạt tròn và hình vành khuyên

Khái niệm hình quạt tròn

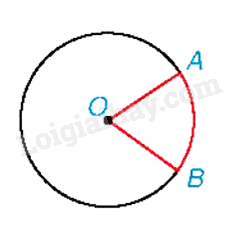
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó.

Khái niệm hình vành khuyên

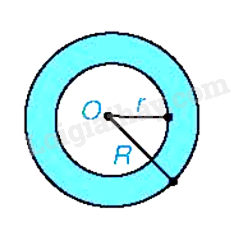
Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là hai đường tròn đồng tâm)

Diện tích hình quạt tròn

Diện tích hình vành khuyên

Tỉ số giữa diện tích hình quạt tròn ứng với cung $n^0$ và diện tích hình tròn (cùng bán kính) đúng bằng $\frac{n}{360}$ và bằng tỉ số giữa độ dài cung $n^0$ và độ dài đường tròn.

Ví dụ:

1. Diện tích hình quạt tròn có độ dài tương ứng với nó là $l=4\pi$cm, bán kính là R = 5cm là:

$S_q=\frac{l.R}{2}=\frac{4\pi .5}{2}=10\pi \left(c{m}^2\right)$

2. Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:

$S_v=\pi \left(5^2-3^2\right)=16\pi \left(m^2\right)$

Xem thêm các bài giải SBT Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Bài 13: Mở đầu về đường tròn

Bài 14: Cung và dây của một đường tròn

Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Bài 16: Vị trí tương đối của đường thẳng và đường tròn

Bài 17: Vị trí tương đối của hai đường tròn

Bài tập cuối chương 5