Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 17: Vị trí tương đối của hai đường tròn chi tiết sách Toán 9 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 17: Vị trí tương đối của hai đường tròn

1. Hai đường tròn cắt nhau

HĐ1 trang 104 Toán 9 Tập 1: Cho hình 5.31, trong đó giả sử O'A < OA.

Ta có: OA – O'A < OO' < OA + O'A. Hãy vẽ hai đường tròn (O; OA) và (O'; O'A) và cho biết hai đường tròn này có mấy điểm chung?

Lời giải:

Theo đề bài, OA – O'A < OO' < OA + O'A nên hai đường tròn (O) và (O') cắt nhau.

Vậy hai đường tròn (O; OA) và (O'; O'A) có hai điểm chung.

Luyện tập 1 trang 105 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) và điểm I cách O một khoảng 2 cm. Xác định vị trí tương đối của đường tròn đã cho và đường tròn (I; r) trong mỗi trường hợp sau:

a) r = 4 cm;

b) r = 6 cm.

Lời giải:

a) Ta có: OI = 2 (cm);

R – r = 5 – 4 = 1 (cm) ;

R + r = 5 + 4 = 9 (cm).

Mà 1 < 2 < 9 nên R – r < OI < R + r.

Suy ra hai đường tròn cắt nhau.

a) Ta có: OI = 2 (cm) ; r – R = 6 – 5 = 1 (cm) ; R + r = 6 + 5 = 11 (cm).

Mà 1 < 2 < 11 nên r – R < OI < R + r.

2. Hai đường tròn tiếp xúc nhau

HĐ2 trang 105 Toán 9 Tập 1: Trên hình 5.33a, ta có OO' = OA + O'A; trên Hình 5.33b, ta có OO' = OA. Trong mỗi trường hợp, hãy vẽ hai đường tròn (O; OA) và (O; O'A) và cho biết hai đường tròn đó có mấy điểm chung?

Lời giải:

• Trường hợp a) vẽ hai đường tròn (O; OA) và (O; O'A). Ta thu được hình vẽ như bên dưới.

Ta thấy hai đường tròn trong trường hợp này có 1 điểm chung.

• Trường hợp b) vẽ hai đường tròn (O; OA) và (O; O'A). Ta thu được hình vẽ như bên dưới.

Ta thấy hai đường tròn trong trường hợp này có 1 điểm chung.

Vậy cả hai trường hợp a) và b) hai đường tròn đều có 1 điểm chung.

Luyện tập 2 trang 105 Toán 9 Tập 1: Cho hai điểm O và O' sao cho OO' = 3 cm. Giải thích tại sao hai đường tròn (O; 8 cm) và (O' ; 5 cm) tiếp xúc với nhau. Chúng tiếp xúc trong hay tiếp xúc ngoài?

Lời giải:

Ta có: R = 8, R' = 5 cm, OO' = 3 cm.

Vì R – R' = 8 – 5 = 3 = OO' nên hai đường tròn tiếp xúc ngoài.

3. Hai đường trong không giao nhau

HĐ3 trang 106 Toán 9 Tập 1: Trên hình 5.35a, ta có OO' > OA + OB, trên Hình 5.35b, ta có OO' < OA – O'B. Trong mỗi trường hợp, hãy vẽ hai đường tròn (O; OA) và (O' ; OB) và cho biết hai đường tròn đó có điểm chung nào không.

Lời giải:

• Trường hợp a) vẽ hai đường tròn (O; OA) và (O' ; OB). Ta thu được hình vẽ như bên dưới.

Ta thấy hai đường tròn trong trường hợp này không có điểm chung.

• Trường hợp b) vẽ hai đường tròn (O; OA) và (O' ; OB). Ta thu được hình vẽ như bên dưới.

Ta thấy hai đường tròn trong trường hợp này không có điểm chung.

Vậy cả hai trường hợp a) và b) hai đường tròn đều không có điểm chung.

Luyện tập 3 trang 106 Toán 9 Tập 1: Cho hai điểm O và O' sao cho OO' = 2 cm. Xác định vị trí tương đối của hai đường tròn (O; 5 cm) và (O' ; r) , biết rằng r < 3 cm.

Lời giải:

Vì R – OO' = 5 – 2 = 3 (cm) > r nên R – r > OO'.

Do đó đường tròn (O; R) đựng đường tròn (O; r).

Thực hành trang 106 Toán 9 Tập 1: Để mô phỏng nguyệt thực, hãy cắt hai hình tròn từ giấy: hình tròn thứ nhất màu sáng tượng trưng cho Mặt Trăng, hình tròn thứ hai màu tối (to hơn bằng giấy mờ càng tốt) tượng trưng cho bóng Trái Đất. Sắp xếp hai hình tròn để:

a) Mô phỏng nguyệt thực một phần. Khi đó, hình ảnh của hai đường tròn có vị trí tương đối như thế nào?

b) Mô phỏng nguyệt thực toàn phần. Khi đó, hình ảnh của hai đường tròn có vị trí tương đối như thế nào?

Lời giải:

a) Mô phỏng nguyệt thực một phần: Dùng đèn pin loại nhỏ chiếu vào Trái đất, đặt Mặt trăng đằng phía sau hình tròn Trái đất sao sao một phần bóng của rái đất in lên hình tròn biểu tượng mặt trăng ta thu được hình ảnh nguyệt thực.

Khi nguyệt thực một phần, hai đường tròn sẽ cắt nhau.

b) Mô phỏng nguyệt thực toàn phần:

Dùng đèn pin loại nhỏ chiếu vào Trái đất, đặt Mặt trăng đằng phía sau hình tròn Trái đất sao sao toàn bộ bóng của Trái đất in lên hình tròn biểu tượng Mặt trăng ta thu được hình ảnh nguyệt thực.

Khi nguyệt thực toàn phần, hai đường tròn không giao nhau: Hai đường tròn đựng nhau.

Tranh luận trang 107 Toán 9 Tập 1: Tròn cho rằng: Nói “hai đường tròn không cắt nhau” cũng có nghĩa là “hai đường tròn không giao nhau”. Theo em, Tròn đúng hay sai?

Lời giải:

Tròn trả lời sai vì hai đường tròn không cắt nhau thì hai đường tròn có thể tiếp xúc nhau hoặc không giao nhau.

Bài tập

Bài 5.24 trang 107 Toán 9 Tập 1: Hình 5.37 cho thấy hình ảnh của những đường tròn qua cách trình bày một số sản phẩm mây tre đan. Bằng cách đánh số các đường tròn, em hãy chỉ ra một vài cặp đường tròn cắt nhau và cặp đường tròn không giao nhau.

Lời giải:

Ta đánh số các đường tròn như hình dưới đây.

Từ hình vẽ trên, ta có:

− Một vài cặp đường tròn cắt nhau: 2 và 3; 4 và 5; 7 và 8; 6 và 9.

− Một vài cặp đường tròn không giao nhau: 1 và 2; 1 và 3; 2 và 5; 3 và 6; 5 và 8; …

Bài 5.25 trang 107 Toán 9 Tập 1: Cho hai điểm O và O' cách nhau một khoảng 5 cm. Mỗi đường tròn sau đây có vị trí tương đối như thế nào đối với đường tròn (O; 3 cm).

a) Đường tròn (O'; 3 cm).

b) Đường tròn (O' ; 1 cm).

c) Đường tròn (O'; 8 cm).

Lời giải:

Ta có: OO' = 5 cm.

a) Vì 3 – 3 < 5 < 3 + 3 nên hai đường tròn (O; 3 cm) và (O'; 3 cm) cắt nhau.

b) Vì 5 > 3 – 1 nên hai đường tròn (O; 3 cm) và (O'; 1 cm) nằm ngoài nhau.

c) Vì 5 = 8 – 3 nên hai đường tròn (O; 3 cm) và (O'; 8 cm) tiếp xúc trong.

Bài 5.26 trang 107 Toán 9 Tập 1: Cho ba điểm thẳng hàng O, A và O'. Với mỗi trường hợp sau, hãy viết hệ thức giữa các độ dài OO', OA và O'A rồi xét xem hai đường tròn (O; OA) và (O'; O'A) tiếp xúc trong hay tiếp xúc ngoài với nhau; vẽ hình để khẳng định dự đoán của mình.

a) Điểm A nằm giữa hai điểm O và O';

b) Điểm O nằm giữa hai điểm A và O';

c) Điểm O' nằm giữa hai điểm A và O.

Lời giải:

a) Nếu điểm A nằm giữa hai điểm O và O' thì OO' = OA + O'A.

Do đó (O; OA) và (O'; O'A) tiếp xúc ngoài.

b) Nếu điểm O nằm giữa hai điểm A và O’ thì OO' = O'A – OA.

Do đó (O; OA) và (O'; O'A) tiếp xúc trong.

c) Nếu điểm O' nằm giữa hai điểm A và O thì OO' = OA – O'A.

Do đó (O; OA) và (O'; O'A) tiếp xúc trong.

Bài 5.27 trang 107 Toán 9 Tập 1: Cho hai đường tròn (O) và (O') tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O') tại C. Chứng minh rằng OB // O'C.

Lời giải:

Vì OA = OB nên tam giác OAB cân tại O, suy ra $\widehat{OBA}=\widehat{OAB}$ .

Vì O'A = O'C nên tam giác O'AC cân tại O, suy ra $\widehat{O^{\text{'}}AC}=\widehat{O^{\text{'}}CA}$ .

Lại có $\widehat{OAB}=\widehat{O^{\text{'}}AB}$  nên $\widehat{OBA}=\widehat{O^{\text{'}}CA}$ .

Vậy OB // O'C.

Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Bài 16. Vị trí tương đối của đường thẳng và đường tròn

Bài 17. Vị trí tương đối của hai đường tròn

Luyện tập chung trang 108

Bài tập cuối chương 5

Pha chế dung dịch theo nồng độ yêu cầu

Tính chiều cao và xác định khoảng cách

Lý thuyết Vị trí tương đối của hai đường tròn

1. Hai đường tròn cắt nhau

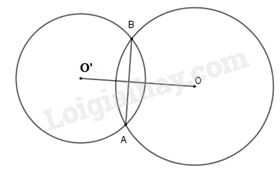
Hai đường tròn (O;R) và (O;R’) cắt nhau khi

$R-R^{\prime }<O{O}^{\prime }<R+R^{\prime }$ (với $R>R^{\prime }$)

Ví dụ: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:

4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.

2. Hai đường tròn tiếp xúc với nhau

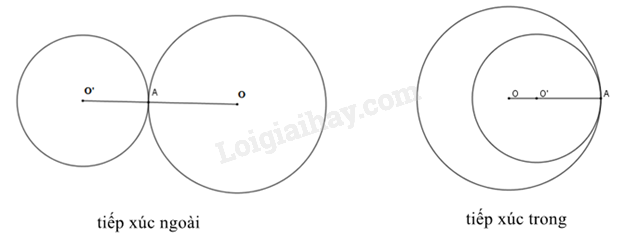
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài khi $O{O}^{\prime }=R+R^{\prime }$.

+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc trong khi $O{O}^{\prime }=R-R^{\prime }\left(R>R^{\prime }\right)$.

Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.

Ví dụ:

Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.

Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.

3. Hai đường tròn không giao nhau

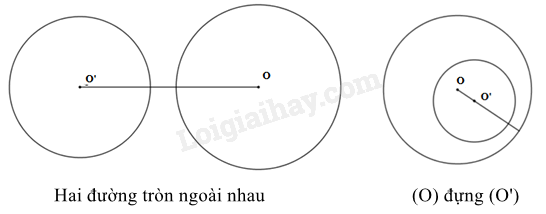
- Hai đường tròn (O;R) và (O’;R’) ngoài nhau khi $O{O}^{\prime }>R+R^{\prime }$;

- Đường tròn (O;R) đựng đường tròn (O’;R’) khi $R>R^{\prime }$ và $O{O}^{\prime }<R-R^{\prime }$.

Khi O trùng với O’ và $R\ne R^{\prime }$ thì ta có hai đường tròn đồng tâm.

Ví dụ: Cho đường tròn (O;3cm) và (O’;4cm) có $O{O}^{\prime }>8cm$ thì $O{O}^{\prime }=8cm>3cm+4cm=R+R^{\prime }$ nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.

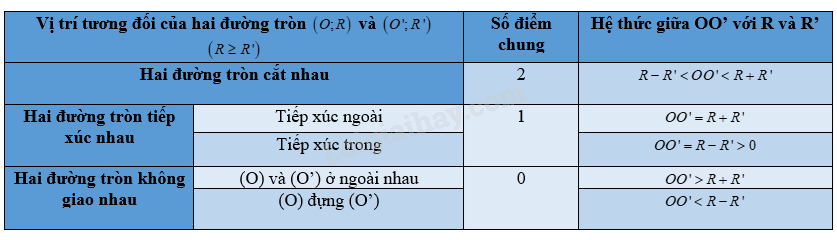
Bảng tổng kết vị trí tương đối của hai đường tròn