Bài 3 trang 65 Toán 10 Tập 1 | Chân trời sáng tạo Giải Toán lớp 10

Nguyễn Linh Anh Ngày: 23-08-2024 Lớp 10

4 K

Với giải Bài 3 trang 65 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180

Bài 3 trang 65 Toán lớp 10: Tìm α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:

a) cosα = $\frac{- \sqrt{2}}{2}$ ;

b) sinα = 0;

c) tanα = 1;

d) cotα không xác định.

Phương pháp giải:

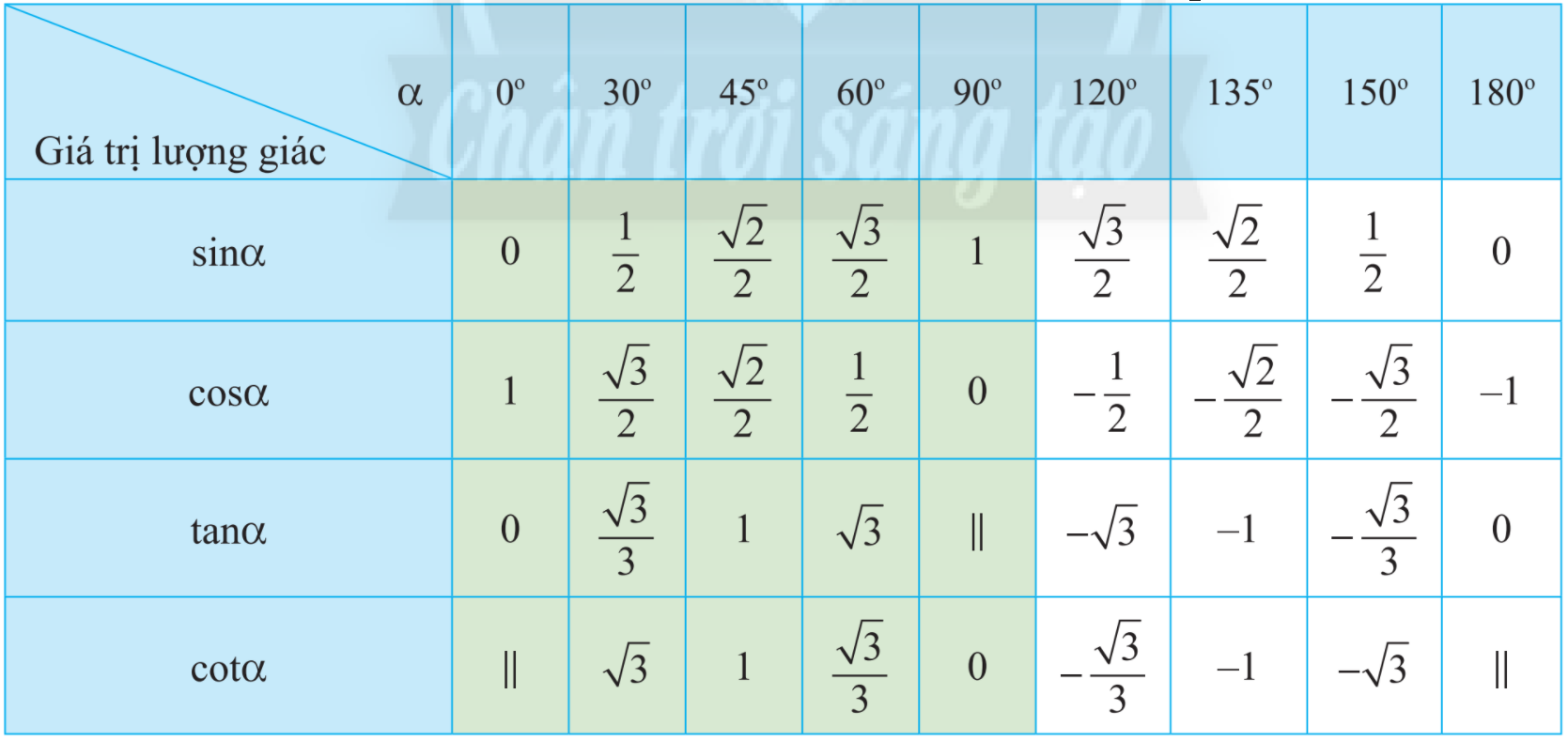
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt để tìm góc.

Lời giải:

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cos α$ ta có:

$\cos α = \frac{- \sqrt{2}}{2}$ với $α = 135^{o}$

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\sin α$ ta có:

$\sin α = 0$ với $α = 0^{o}$ và $α = 180^{o}$

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\tan α$ ta có:

$\tan α = 1$ với $α = 45^{o}$

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cot α$ ta có:

$\cot α$ không xác định với $α = 0^{o}$

Bài tập vận dụng:

Bài 1. Tính giá trị biểu thức:

a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°.

b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°;

c) $C = s i n (180 ° - x) - c o s (90 ° - x) + s i n^{2} x . \frac{1}{\sin^{2} (90 ° - x)} - t a n^{2} x .$

Hướng dẫn giải

a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°

$A = \frac{1}{2} . \frac{\sqrt{2}}{2} . \frac{\sqrt{3}}{2} - (- \frac{1}{2}) . (- 1) . (- \sqrt{3})$

$A = \frac{\sqrt{6}}{8} + \frac{\sqrt{3}}{2}$

$A = \frac{\sqrt{6} + 4 \sqrt{3}}{8}$

b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°

B = (cos0° + cos180°) + (cos20° + cos160°) + … + (cos80° + cos100°)

B = (cos0° ‒ cos0°) + (cos20° ‒ cos20°) + … + (cos80° ‒ cos80°) (hai góc bù nhau)

B = 0.

c) $C = s i n (180 ° - x) - c o s (90 ° - x) + s i n^{2} x . \frac{1}{\sin^{2} (90 ° - x)} - t a n^{2} x .$ $C = \sin x - \sin x + s i n^{2} x . \frac{1}{{cos}^{2} x} - t a n^{2} x$

C = 0 + tan2x ‒ tan2x

C = 0.

Bài 2. Cho góc α (0° ≤ α ≤ 180°) với $\tan α = - \sqrt{3}$ . Tính giá trị biểu thức: $M = c o s α + c o t^{2} α - \frac{1}{\sin^{2} α} .$

Hướng dẫn giải

Với $\tan α = - \sqrt{3}$ ta có α = 120°.

Suy ra: $s i n α = \frac{\sqrt{3}}{2}; c o s α = - \frac{1}{2}; \cot α = - \frac{\sqrt{3}}{3} .$

Do đó:
$M = c o s α + c o t^{2} α - \frac{1}{\sin^{2} α}$
$M = - \frac{1}{2} + {(- \frac{\sqrt{3}}{3})}^{2} - \frac{1}{{(\frac{\sqrt{3}}{2})}^{2}}$
$M = - \frac{1}{2} + \frac{1}{3} - \frac{4}{3}$
$M = - \frac{3}{2} .$

Vậy $M = - \frac{3}{2} .$

Bài 3.

a) Chứng minh rằng với mọi góc 0° ≤ α ≤ 180° ta luôn có: sin2α + cos2α = 1.

b) Cho tam giác ABC. Chứng minh rằng:

$\frac{\sin^{3} \frac{B}{2}}{c o s (\frac{A + C}{2})} + \frac{c o s^{3} \frac{B}{2}}{\sin (\frac{A + C}{2})} - \frac{c o s (A + C)}{\sin B} . \tan B = 2.$

Hướng dẫn giải

a) Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho $\hat{x O M} = α$ . Gọi ( $x_{0}$ ; $y_{0}$ ) là toạ độ điểm M, ta có:

- Tung độ $y_{0}$ của M là sin của góc α, kí hiệu là sinα = $y_{0}$ ;

- Hoành độ $x_{0}$ của M là côsin của góc α, kí hiệu là cosα = $x_{0}$ ;

Gọi H và K lần lượt là hình chiếu của M lên Ox và Oy.
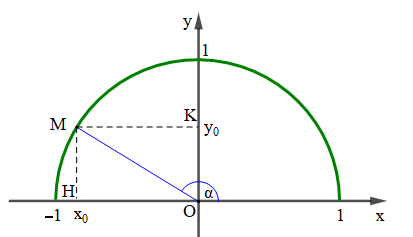Khi đó ta có: OH = $x_{0}$ = cosα, MH = OK = $y_{0}$ = sinα, OM = 1.

Tam giác OMH vuông tại H, áp dụng định lí Pythagore ta có:

$M H^{2} + O H^{2} = O M^{2}$

Hay sin2α + cos2α = 1.

Vậy sin2α + cos2α = 1.

b) Vì $\hat{A} + \hat{B} + \hat{C}$ = 180° (định lí tổng ba góc trong tam giác) nên: $\hat{A} + \hat{C}$ = 180° ‒ $\hat{B}$ .

Suy ra $\frac{\hat{A} + \hat{C}}{2} = \frac{180 ° - \hat{B}}{2} = 90 ° - \frac{\hat{B}}{2}$ .

Ta có:

$\frac{\sin^{3} \frac{B}{2}}{c o s (\frac{A + C}{2})} + \frac{c o s^{3} \frac{B}{2}}{\sin (\frac{A + C}{2})} - \frac{c o s (A + C)}{\sin B} . \tan B$ $= \frac{\sin^{3} \frac{B}{2}}{c o s (90 ° - \frac{B}{2})} + \frac{c o s^{3} \frac{B}{2}}{\sin (90 ° - \frac{B}{2})} - \frac{c o s (180 ° - B)}{\sin B} . \tan B$

$= \frac{\sin^{3} \frac{B}{2}}{\sin \frac{B}{2}} + \frac{c o s^{3} \frac{B}{2}}{c o s \frac{B}{2}} - \frac{- \cos B}{\sin B} . \tan B$

$= \sin^{2} \frac{B}{2} + c o s^{2} \frac{B}{2} + \frac{\cos B}{\sin B} . \tan B$

$= (\sin^{2} \frac{B}{2} + c o s^{2} \frac{B}{2}) + \frac{\cos B}{\sin B} . \frac{\sin B}{\cos B}$

= 1 + 1 (do sin2α + cos2α = 1 theo câu a)

= 2

Vậy $\frac{\sin^{3} \frac{B}{2}}{c o s (\frac{A + C}{2})} + \frac{c o s^{3} \frac{B}{2}}{\sin (\frac{A + C}{2})} - \frac{c o s (A + C)}{\sin B} . \tan B = 2.$