Với HĐ Khám phá 2 giải trang 49 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 2: Hàm số bậc hai học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Hàm số bậc hai
HĐ Khám phá 2 trang 49 Toán lớp 10:
a) Xét hàm số có bảng giá trị:
|
2 |
3 |
4 |
5 |
6 |
|
|
7 |
4 |
3 |
4 |
7 |
Trên mặt phẳng tọa độ, ta có các điểm với x thuộc bảng giá trị đã cho (hình 1).
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số trên Hình 1.
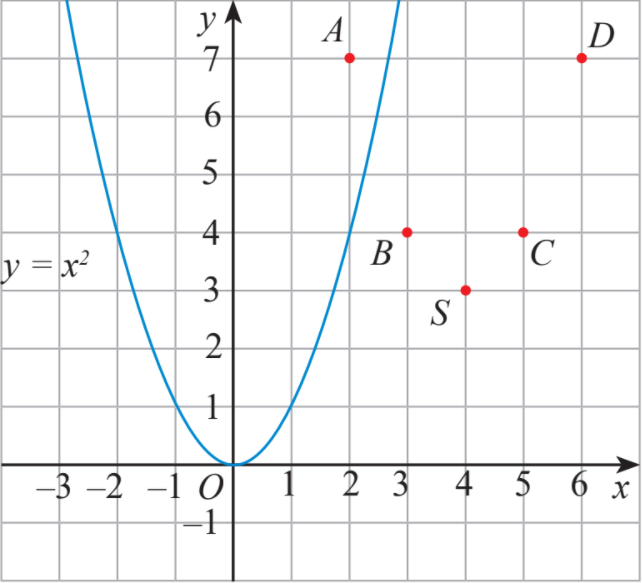
b) Tương tự xét hàm số có bảng giá trị:
|
2 |
3 |
4 |
5 |
6 |
|
|
-1 |
2 |
3 |
2 |
-1 |
Trên mặt phẳng tọa độ, ta có các điểm với x thuộc bảng giá trị đã cho (hình 2).
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số trên Hình 2.
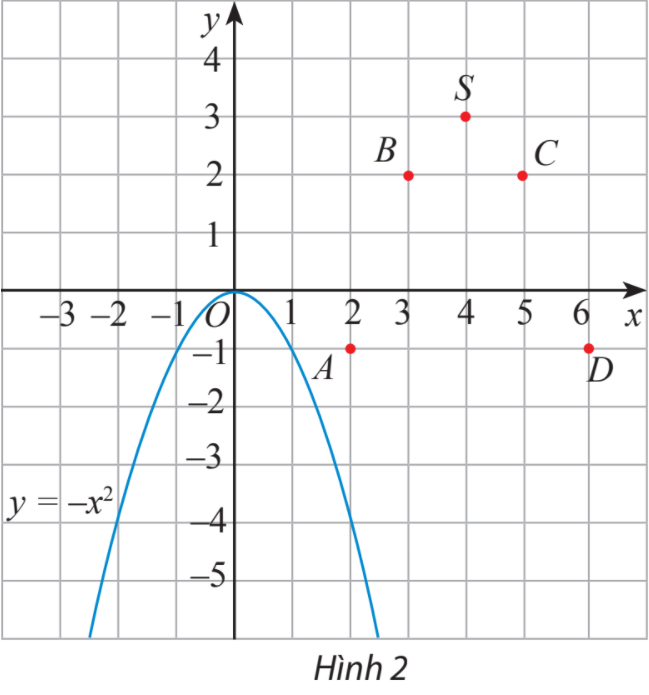
Lời giải:
a)
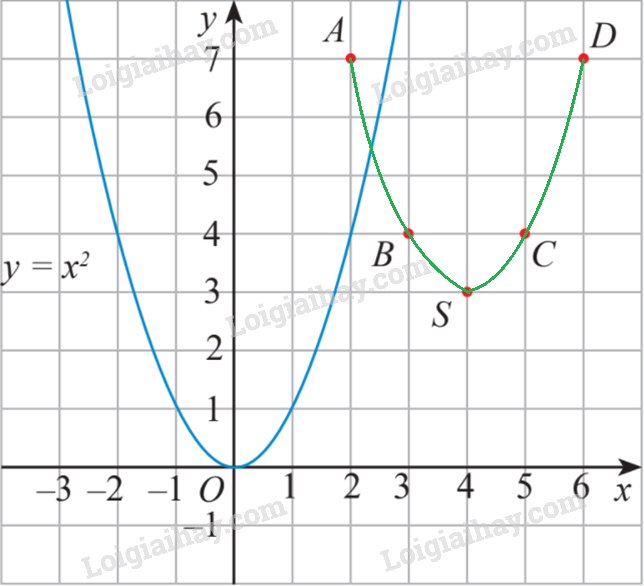
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số , cùng có bề lõm quay lên trên.
b)
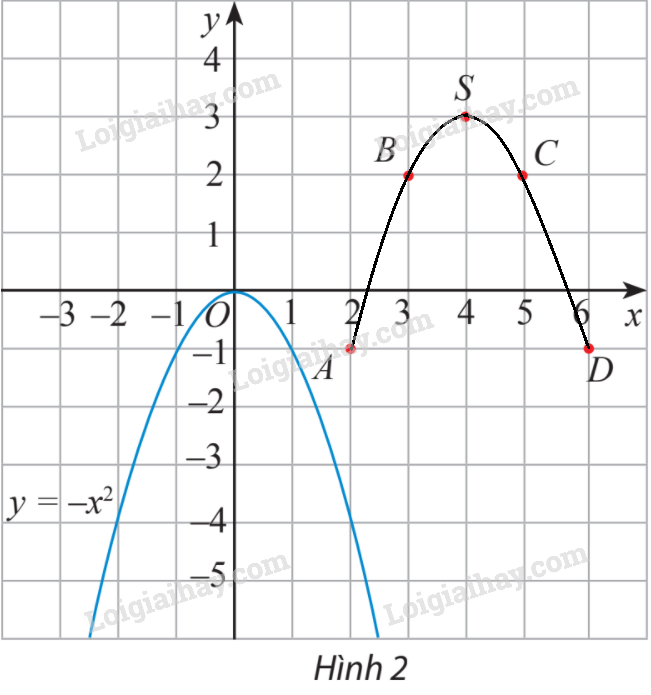
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số , cùng có bề lõm quay xuống dưới.
Lý thuyết Đồ thị hàm số bậc hai
- Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một parabol (P):
+ Có đỉnh S với hoành độ , tung độ ; (Δ = b2 – 4ac)
+ Có trục đối xứng là đường thẳng (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên nếu a > 0, quay xuống dưới nếu a < 0;
+ Cắt trục tung tại điểm có tung độ bằng c, tức là đồ thị đi qua điểm có tọa độ (0; c).
Chú ý:
+ Nếu b = 2b’ thì (P) có đỉnh S .
+ Nếu phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2 thì đồ thị hàm số bậc hai y = ax2 + bx + c cắt trục hoành tại hai điểm lần lượt có hoành độ là hai nghiệm này.
Ví dụ: Cho hàm số bậc hai y = x2 + 2x + 1.
Ta xác định a = 1; b = 2; c = 1; Δ = b2 – 4ac = 0.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = x2 + 2x + 1 là một parabol (P):
+ Có đỉnh S với hoành độ , tung độ ;
+ Có trục đối xứng d là đường thẳng x = ‒1 (đường thẳng này đi qua đỉnh S(‒1; 0) và song song với trục Oy);
+ Bề lõm của parabol quay lên trên do a = 1 > 0;
+ Cắt trục tung tại điểm có tung độ bằng 1, tức là đồ thị đi qua điểm có toạ độ (0; 1).
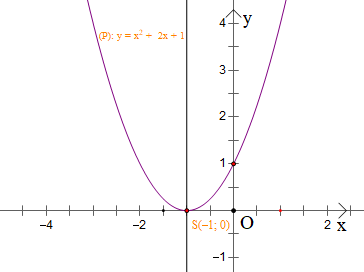
Đối với hàm số bậc hai y = x2 + 2x + 1 ta thấy hệ số b = 2 là số chẵn nên cũng có thể tìm toạ độ đỉnh với a = 1, b' = 1, c = 1 và Δ' = b'2 – ac = 0.
Khi đó ta cũng tìm được S(‒1; 0).
*Cách vẽ đồ thị hàm số bậc hai:
Cách vẽ đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0):
- Xác định tọa độ đỉnh S.
- Vẽ trục đối xứng d là đường thẳng x = .
- Tìm tọa độ giao điểm của đồ thị với trục tung (điểm A(0; c)) và giao điểm của đồ thị với trục hoành (nếu có).
Xác định thêm điểm đối xứng với A qua trục đối xứng d, là điểm B.
- Vẽ parabol có đỉnh S, có trục đối xứng d, đi qua các điểm tìm được.
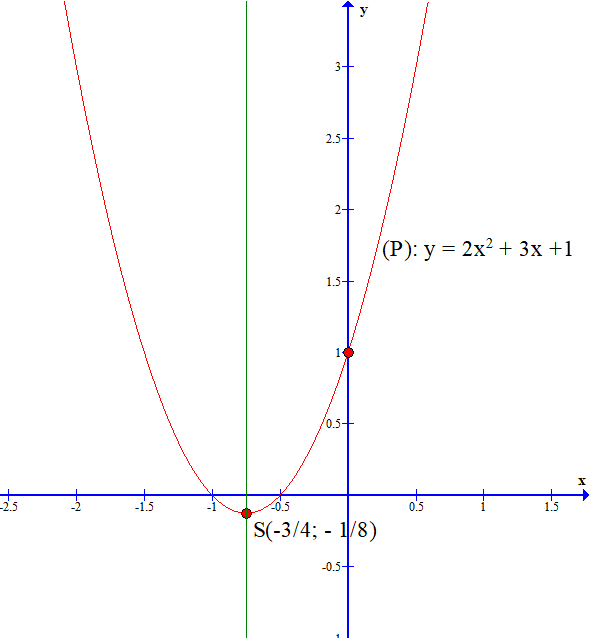
Ví dụ: Vẽ đồ thị hàm số bậc hai y = 2x2 + 3x + 1.
Ta có: a = 2; b = 3; c = 1; Δ = b2 – 4ac = 1.
Trong mặt phẳng toạ độ Oxy, đồ thị hàm số bậc hai y = 2x2 + 3x + 1 là một parabol (P):
+ Có toạ độ đỉnh S với tung độ hay ;
+ Có trục đối xứng là đường thẳng x = (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm của parabol (P) quay lên trên do a = 2 > 0;
+ Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1, tức là đồ thị (P) đi qua điểm có tọa độ (0; 1)
Ngoài ra phương trình 2x2 + 3x + 1 = 0 có hai nghiệm phân biệt là x1 = ‒1 và nên đồ thị hàm số cắt trục hoành tại hai điểm có toạ độ (‒1; 0) và
Ta vẽ đồ thị hàm số y = 2x2 + 3x + 1 như hình vẽ dưới đây:
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
HĐ Khởi động trang 49 Toán lớp 10: Các hàm số này có chung đặc điểm gì?...
Bài 1 trang 56 Toán lớp 10: Hàm số nào sau đây là hàm số bậc hai?...
Bài 2 trang 56 Toán lớp 10: Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai...
Bài 4 trang 56 Toán lớp 10: Cho hàm số bậc hai có f(0)=1, f(1)=2, f(2)=5...
Bài 6 trang 56 Toán lớp 10: Vẽ đồ thị các hàm số sau:...
Bài 7 trang 56 Toán lớp 10: Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12...
Bài 8 trang 57 Toán lớp 10: Tìm công thức của hàm số bậc hai có đồ thị như Hình 13...
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của một góc từ 00 đến 1800
Bài 2: Định lí cosin và định lí sin