Giải SGK Toán 7 Bài 1 (Chân trời sáng tạo): Các góc ở vị trí đặc biệt

Nguyễn Linh Anh Ngày: 26-08-2024 Lớp 7

8.1 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 1: Các góc ở vị trí đặc biệt chi tiết sách Toán 7 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 1: Các góc ở vị trí đặc biệt

1. Hai góc kề bù

Giải Toán 7 trang 69 Tập 1

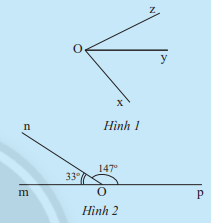
HĐ 1 trang 69 Toán lớp 7: a) Quan sát Hình 1 và cho biết hai góc $\hat{x O y}$ và $\hat{y O z}$ có:

- Cạnh nào chung?

- Điểm trong nào chung?

b) Hãy đo các góc $\hat{x O y}, \hat{y O z}, \hat{x O z}$ trong Hình 1 rồi so sánh tổng số đo của $\hat{x O y}$ và $\hat{y O z}$ với $\hat{x O z}$ .

c) Tính tổng số đo của hai góc $\hat{m O n}$ và $\hat{n O p}$ trong Hình 2.

Phương pháp giải:

Quan sát, đo và tính

Lời giải:

a) Hai góc $\hat{x O y}$ và $\hat{y O z}$ có cạnh Oy chung, không có điểm trong chung

b) Ta có:

$\begin{array}{l} \hat{x O y} = 30^{\circ}, \hat{y O z} = 45^{\circ}, \hat{x O z} = 75^{\circ} \\ \Rightarrow \hat{x O y} + \hat{y O z} = \hat{x O z} \end{array}$

c) Ta có: $\hat{m O n} + \hat{n O p} = 33^{\circ} + 147^{\circ} = 180^{\circ}$

Thực hành 1 trang 69 Toán lớp 7: Quan sát hình 5.

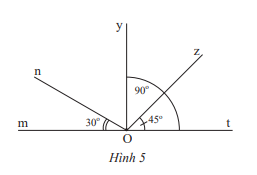
a) Tìm các góc kề với $\hat{t O z}$

b) Tìm số đo của góc kề bù với $\hat{m O n}$ .

c) Tìm số đo của $\hat{n O y}$

d) Tìm số đo của góc kề bù với $\hat{t O z}$ .

Phương pháp giải:

Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.

2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ

Lời giải:

a) Các góc kề với $\hat{t O z}$ là: $\hat{z O y}, \hat{z O n}, \hat{z O m}$

b) Ta có: $\hat{m O n}$ = 30 $^{\circ}$ nên góc kề bù với $\hat{m O n}$ có số đo là: 180 $^{\circ}$ - 30 $^{\circ}$ = 150 $^{\circ}$

c) Ta có:

$\begin{array}{l} \hat{m O n} + \hat{n O y} + \hat{y O t} = 180^{\circ} \\ \Rightarrow 30^{\circ} + \hat{n O y} + 90^{\circ} = 180^{\circ} \\ \Rightarrow \hat{n O y} = 180^{\circ} - 30^{\circ} - 90^{\circ} = 60^{\circ} \end{array}$

Vậy $\hat{n O y} = 60^{\circ}$

d) Ta có: $\hat{t O z} = 45^{\circ}$ nên góc kề bù với $\hat{t O z}$ có số đo là: 180 $^{\circ}$ - 45 $^{\circ}$ = 135 $^{\circ}$

Giải Toán 7 trang 70 Tập 1

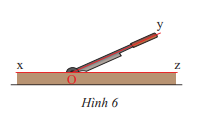
Vận dụng 1 trang 70 Toán lớp 7: Hình 6 mô tả con dao và bàn cắt. Hãy tìm hai góc kề bù có trong hình

Phương pháp giải:

Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.

2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ

2 góc vừa kề vừa bù nhau thì là hai góc kề bù

Lời giải:

2 góc kề bù trong hình là $\hat{x O y}$ và $\hat{y O z}$

2. Hai góc đối đỉnh

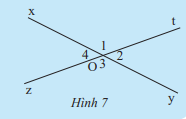
HĐ 2 trang 70 Toán lớp 7: Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. Hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của $\hat{O_{1}}$ và $\hat{O_{3}}$ .

Phương pháp giải:

Xác định các cạnh và đỉnh của các góc $\hat{O_{1}}$ và $\hat{O_{3}}$ .

Lời giải:

$\hat{O_{1}}$ có cạnh Ox và Ot, đỉnh O

$\hat{O_{3}}$ có cạnh Oy và Oz, đỉnh O

Ta có: $\hat{O_{1}}$ và $\hat{O_{3}}$ có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.

$\hat{O_{1}}$ và $\hat{O_{3}}$ có chung đỉnh

Thực hành 2 trang 70 Toán lớp 7: a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ

b) Vẽ $\hat{x O y}$ rồi vẽ $\hat{t O z}$ đối đỉnh với $\hat{x O y}$

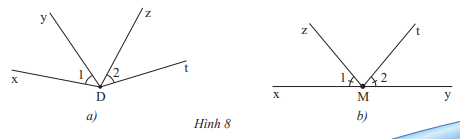
c) Cặp góc $\hat{x D y}$ và $\hat{z D t}$ trong Hình 8a và cặp góc $\hat{x M z}$ và $\hat{t M y}$ trong Hình 8b có phải là các cặp góc đối đỉnh hay không? Hãy giải thích tại sao.

Phương pháp giải:

Vẽ hình

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia

Lời giải:

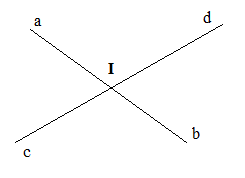
Các cặp góc đối đỉnh trên hình vẽ là: $\hat{a I d}$ và $\hat{b I c}$ ; $\hat{a I c}$ và $\hat{b I d}$

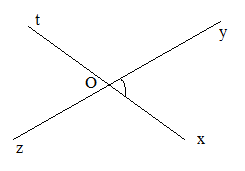
Bước 1: Vẽ góc $\hat{x O y}$

Bước 2: Vẽ tia Ot là tia đối của tia Ox

Bước 3: Vẽ tia Oz là tia đối của tia Oy

Ta được $\hat{t O z}$ đối đỉnh với $\hat{x O y}$

c) Cặp góc $\hat{x D y}$ và $\hat{z D t}$ trong Hình 8a và cặp góc $\hat{x M z}$ và $\hat{t M y}$ trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia

Ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy

Ở Hình 8b, My là tia đối của Mx nhưng Mt không là tia đối của Mz

Chú ý: 2 đường thẳng cắt nhau tạo ra 2 cặp góc đối đỉnh

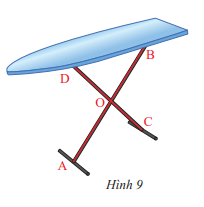
Vận dụng 2 trang 70 Toán lớp 7: Hai chân chống AB và CD của cái bàn xếp ở Hình 9 cho ta hình ảnh hai đường thẳng cắt nhau tại điểm O. Hãy chỉ ra các góc đối đỉnh trong hình

Phương pháp giải:

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia

Lời giải:

Các góc đối đỉnh trong hình là: $\hat{D O B}$ và $\hat{C O A}$ ; $\hat{B O C}$ và $\hat{A O D}$

3. Tính chất của hai góc đối đỉnh

Giải Toán 7 trang 71 Tập 1

HĐ 3 trang 71 Toán lớp 7: Quan sát Hình 10.

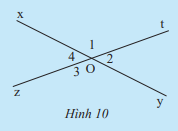
a) Hãy dùng thước đo góc để đo $\hat{O_{1}}$ và $\hat{O_{3}}$ . So sánh số đo hai góc đó.

b) Hãy dùng thước đo góc để đo $\hat{O_{2}}$ và $\hat{O_{4}}$ . So sánh số đo hai góc đó.

Phương pháp giải:

Đo góc bằng thước đo góc

Lời giải:

Ta có:

$\begin{array}{l} a) \hat{O_{1}} = 135^{\circ}; \hat{O_{3}} = 135^{\circ} \Rightarrow \hat{O_{1}} = \hat{O_{3}} \\ b) \hat{O_{2}} = 45^{\circ}; \hat{O_{4}} = 45^{\circ} \Rightarrow \hat{O_{2}} = \hat{O_{4}} \end{array}$

Thực hành 3 trang 71 Toán lớp 7: Quan sát hình 12

a) Tìm góc đối đỉnh của $\hat{y O v}$

b) Tính số đo của $\hat{u O z}$

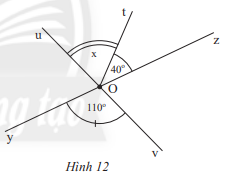
Phương pháp giải:

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia

Hai góc đối đỉnh có số đo bằng nhau

Lời giải:

a) Góc đối đỉnh của $\hat{y O v}$ là $\hat{z O u}$ vì tia Oz đối tia Oy, Ou đối tia Ov

b) Ta có: $\hat{u O z} = \hat{y O v}$ ( 2 góc đối đỉnh), mà $\hat{y O v} = 110^{\circ}$ nên $\hat{u O z} = 110^{\circ}$

Vận dụng 3 trang 71 Toán lớp 7: Tìm số đo x của $\hat{u O t}$ trong Hình 12.

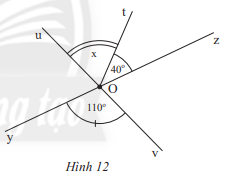
Phương pháp giải:

Bước 1: Tìm số đo $\hat{u O z}$

Bước 2: $\hat{u O t} + \hat{t O z} = \hat{u O z}$ do $\hat{u O t}, \hat{t O z}$ là 2 góc kề nhau

Lời giải:

Ta có: $\hat{u O z} = \hat{y O v}$ ( 2 góc đối đỉnh), mà $\hat{y O v} = 110^{\circ}$ nên $\hat{u O z} = 110^{\circ}$

Mà $\hat{u O t}, \hat{t O z}$ là 2 góc kề nhau nên $\hat{u O t} + \hat{t O z} = \hat{u O z}$

$\begin{array}{l} \Rightarrow x + 40^{\circ} = 110^{\circ} \\ \Rightarrow x = 110^{\circ} - 40^{\circ} = 70^{\circ} \end{array}$

Vậy x = 70 $^{\circ}$

Bài tập

Giải Toán 7 trang 72 Tập 1

Bài 1 trang 72 Toán lớp 7: Quan sát Hình 14.

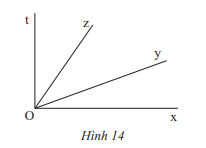
a) Tìm các góc kề với $\hat{x O y}$ .

b) Tìm số đo của $\hat{t O z}$ nếu cho biết $\hat{x O y} = 20^{\circ}; \hat{x O t} = 90^{\circ}; \hat{y O z} = \hat{t O z}$ .

Phương pháp giải:

a) Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.

b) Nếu $\hat{u O t}, \hat{t O z}$ là 2 góc kề nhau thì $\hat{u O t} + \hat{t O z} = \hat{u O z}$

Lời giải:

a) Các góc kề với $\hat{x O y}$ là: $\hat{y O z}; \hat{y O t}$

b) Ta có:

$\begin{array}{l} \hat{x O y} + \hat{y O z} + \hat{z O t} = \hat{x O t} \\ \Rightarrow 20^{\circ} + \hat{z O t} + \hat{z O t} = 90^{\circ} \\ \Rightarrow 2. \hat{z O t} = 90^{\circ} - 20^{\circ} = 70^{\circ} \\ \Rightarrow \hat{z O t} = 70^{\circ} : 2 = 35^{\circ} \end{array}$

Bài 2 trang 72 Toán lớp 7: Cho hai góc $\hat{x O y}, \hat{y O z}$ kề bù với nhau. Biết $\hat{x O y} = 25^{\circ}$ . Tính $\hat{y O z}$ .

Phương pháp giải:

2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ

Lời giải:

Vì hai góc $\hat{x O y}, \hat{y O z}$ kề bù với nhau nên

$\begin{array}{l} \hat{x O y} + \hat{y O z} = 180^{\circ} \\ \Rightarrow 25^{\circ} + \hat{y O z} = 180^{\circ} \\ \Rightarrow \hat{y O z} = 180^{\circ} - 25^{\circ} = 155^{\circ} \end{array}$

Bài 3 trang 72 Toán lớp 7: Cho hai góc kề nhau $\hat{A O B}$ và $\hat{B O C}$ với $\hat{A O C} = 80^{\circ}$ . Biết $\hat{A O B} = \frac{1}{5} . \hat{A O C}$ . Tính số đo các góc $\hat{A O B}$ và BOC

Phương pháp giải:

Nếu $\hat{u O t}, \hat{t O z}$ là 2 góc kề nhau thì $\hat{u O t} + \hat{t O z} = \hat{u O z}$

Lời giải:

Vì $\hat{A O B}$ và $\hat{B O C}$ là 2 góc kề nhau nên $\hat{A O B} + \hat{B O C} = \hat{A O C}$ , mà $\hat{A O C} = 80^{\circ}$ nên $\hat{A O B} + \hat{B O C} = 80^{\circ}$

Vì $\hat{A O B} = \frac{1}{5} . \hat{A O C}$ nên $\hat{A O B} = \frac{1}{5} {.80}^{\circ} = 16^{\circ}$

Như vậy,

$\begin{array}{l} 16^{\circ} + \hat{B O C} = 80^{\circ} \\ \Rightarrow \hat{B O C} = 80^{\circ} - 16^{\circ} = 64^{\circ} \end{array}$

Vậy $\hat{A O B} = 16^{\circ}; \hat{B O C} = 64^{\circ}$

Bài 4 trang 72 Toán lớp 7: Tìm số đo các góc còn lại trong mỗi hình sau:

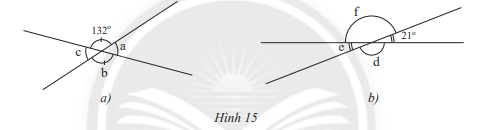
Phương pháp giải:

Sử dụng tính chất:

+ Hai góc đối đỉnh thì bằng nhau

+ Hai góc kề bù có tổng số đo là 180 độ

Lời giải:

a) Ta có: b = 132 $^{\circ}$ ( 2 góc đối đỉnh)

a + 132 $^{\circ}$ =180 $^{\circ}$ (2 góc kề bù) nên a = 180 $^{\circ}$ - 132 $^{\circ}$ = 48 $^{\circ}$

c = a = 48 $^{\circ}$ (2 góc đối đỉnh)

b) e = 21 $^{\circ}$ (2 góc đối đỉnh)

d + 21 $^{\circ}$ =180 $^{\circ}$ (2 góc kề bù) nên a = 180 $^{\circ}$ - 21 $^{\circ}$ = 159 $^{\circ}$

f = d =159 $^{\circ}$ (2 góc đối đỉnh)

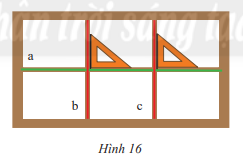
Bài 5 trang 72 Toán lớp 7: Cặp cạnh nào của các ô cửa sổ (Hình 16) vuông góc với nhau? Hãy dùng kí hiệu ( $⊥$ ) để biểu diễn chúng.

Phương pháp giải:

2 đường thẳng cắt nhau tạo thành 1 góc vuông thì 2 đường thẳng đó vuông góc

Lời giải:

Ta thấy: a $⊥$ b và a $⊥$ c

Lý thuyết Các góc ở vị trí đặc biệt

1. Hai góc kề bù

Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.

Hai góc bù nhau là hai góc có tổng số đo bằng 180⁰.

Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.

Ví dụ:

a) Hai góc $\hat{z O y}$ và $\hat{t O y}$ có cạnh chung Oy và không có điểm trong chung. Vì thế, hai góc $\hat{z O y}$ và $\hat{t O y}$ là hai góc kề nhau.

Lý thuyết Toán 7 Chân trời sáng tạo Bài 1: Các góc ở vị trí đặc biệt (ảnh 1)

Lý thuyết Toán 7 Chân trời sáng tạo Bài 1: Các góc ở vị trí đặc biệt (ảnh 2)

Ta có: $\hat{x O z} + \hat{x O y} = 60^{0} + 120^{0} = 180^{0}$ .

Vì vậy, hai góc xOz và góc xOy là hai góc bù nhau.

Mặt khác: hai góc $\hat{x O z}$ và $\hat{x O y}$ có cạnh chung Ox và không có điểm trong chung nên hai góc $\hat{x O z}$ và $\hat{x O y}$ là hai góc kề nhau.

Vậy, hai góc $\hat{x O z}$ và $\hat{x O y}$ là hai góc kề bù.

Chú ý : Nếu M là điểm trong của góc xOy thì $\hat{x O M} + \hat{M O y} = \hat{x O y}$ .

Lý thuyết Toán 7 Chân trời sáng tạo Bài 1: Các góc ở vị trí đặc biệt (ảnh 3)

2. Hai góc đối đỉnh

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Ví dụ :

Lý thuyết Toán 7 Chân trời sáng tạo Bài 1: Các góc ở vị trí đặc biệt (ảnh 4)

Cạnh Oy của $\hat{O_{4}}$ là tia đối của cạnh Ox của _{$\hat{O_{2}}$};

Cạnh Ot của $\hat{O_{4}}$ là tia đối của cạnh Oz của _{$\hat{O_{2}}$};

Vì vậy, _{$\hat{O_{2}}$} và $\hat{O_{4}}$ là hai góc đối đỉnh.

Tương tự, góc $\hat{O_{1}}$ và $\hat{O_{3}}$ cũng là hai góc đối đỉnh.

Chú ý: Khi $\hat{O_{1}}$ và $\hat{O_{3}}$ là hai góc đối đỉnh, ta còn nói $\hat{O_{1}}$ đối đỉnh với $\hat{O_{3}}$ ; $\hat{O_{3}}$ đối đỉnh với $\hat{O_{1}}$ ; $\hat{O_{1}}$ và $\hat{O_{3}}$ đối đỉnh với nhau.