Với giải Hoạt động 6 trang 91 SGK Toán lớp 10 Cánh diều chi tiết trong Bài 5: Tích của một số với một vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 5: Tích của một số với một vectơ

Hoạt động 6 trang 91 Toán lớp 10: Cho ba điểm phân biệt A, B, C.

a) Nếu ba điểm A, B, C thẳng hàng thì hai vectơ $\overrightarrow{AB},\overrightarrow{AC}$ có cùng phương hay không? 

b) Ngược lại, nếu hai vectơ $\overrightarrow{AB},\overrightarrow{AC}$ cùng phương thì ba điểm A, B, C có thẳng hàng hay không? 

Lời giải:

a) Giá của vectơ $\overrightarrow{AB}$ là đường thẳng AB, giá của vectơ $\overrightarrow{AC}$ là đường thẳng AC, mà A,  B, C thẳng hàng nên đường thẳng AB và AC trùng nhau. Do đó hai vectơ $\overrightarrow{AB},\overrightarrow{AC}$ cùng phương. 

b) Hai vectơ $\overrightarrow{AB},\overrightarrow{AC}$ cùng phương khi giá AB và AC của chúng song song hoặc trùng nhau. Trường hợp song song không thể xảy ra do hai đường thẳng AB và AC có chung giao điểm A. Vậy AB trùng với AC hay A, B, C thẳng hàng. 

Lý thuyết Một số ứng dụng

3.1. Trung điểm của đoạn thẳng

Nếu I là trung điểm của đoạn thẳng AB thì $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}=2\overrightarrow{\mathrm{MI}}$ với điểm M bất kì.

Chứng minh:

Vì I là trung điểm của đoạn thẳng AB nên $\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}$ = $\overrightarrow{0}$

Suy ra:

$\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}$ = $\left(\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IA}}\right)+\left(\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IB}}\right)$ 

= $\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}$ = $2\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}$

= $2\overrightarrow{\mathrm{MI}}+\overrightarrow{0}$ = $2\overrightarrow{\mathrm{MI}}$.

⇒ $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}$ = $2\overrightarrow{\mathrm{MI}}$ (đpcm).

Ví dụ: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC, BD. Chứng minh $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}=2\overrightarrow{\mathrm{MN}}$.

Hướng dẫn giải:

Vì M, N lần lượt là trung điểm của AC, BD nên ta có:

$\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MC}}=\overrightarrow{0}$

$\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MD}}=2\overrightarrow{\mathrm{MN}}$

⇒ $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}$ = $\left(\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MC}}\right)+\left(\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MD}}\right)$ = $\overrightarrow{0}+2\overrightarrow{\mathrm{MN}}$ = $2\overrightarrow{\mathrm{MN}}$.

⇒ $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}=2\overrightarrow{\mathrm{MN}}$ (đpcm).

3.2. Trọng tâm của tam giác

Nếu G là trọng tâm của tam giác ABC thì $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}=3\overrightarrow{\mathrm{MG}}$ với điểm M bất kì.

Ví dụ: Gọi G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’. Chứng minh rằng: $\overrightarrow{\text{AA'}}+\overrightarrow{\mathrm{BB}\text{'}}+\overrightarrow{\mathrm{CC}\text{'}}=3\overrightarrow{\mathrm{GG}\text{'}}$.

Hướng dẫn giải:

Vì G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’ nên:

$\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0}$ và $\overrightarrow{\mathrm{GA}\text{'}}+\overrightarrow{\mathrm{GB}\text{'}}+\overrightarrow{\mathrm{GC}\text{'}}=\overrightarrow{0}$

Theo quy tắc cộng vectơ ta có:

$\overrightarrow{\text{AA}\text{'}}=\overrightarrow{\mathrm{AG}}+\overrightarrow{\mathrm{GG}\text{'}}+\overrightarrow{\mathrm{G}\text{'}\mathrm{A}\text{'}}$ (1)

$\overrightarrow{\mathrm{BB}\text{'}}=\overrightarrow{\mathrm{BG}}+\overrightarrow{\mathrm{GG}\text{'}}+\overrightarrow{\mathrm{G}\text{'}\mathrm{B}\text{'}}$ (2)

$\overrightarrow{\mathrm{CC}\text{'}}=\overrightarrow{\mathrm{CG}}+\overrightarrow{\mathrm{GG}\text{'}}+\overrightarrow{\mathrm{G}\text{'}\mathrm{C}\text{'}}$ (3)

Cộng vế với vế của (1), (2) và (3) ta có:

$\overrightarrow{\text{AA'}}+\overrightarrow{\mathrm{BB}\text{'}}+\overrightarrow{\mathrm{CC}\text{'}}$ = $3\overrightarrow{\mathrm{GG}\text{'}}+\left(\overrightarrow{\mathrm{AG}}+\overrightarrow{\mathrm{BG}}+\overrightarrow{\mathrm{CG}}\right)+\left(\overrightarrow{\mathrm{GA}\text{'}}+\overrightarrow{\mathrm{GB}\text{'}}+\overrightarrow{\mathrm{GC}\text{'}}\right)$

= $3\overrightarrow{\mathrm{GG}\text{'}}+\left(-\overrightarrow{\mathrm{GA}}-\overrightarrow{\mathrm{GB}}-\overrightarrow{\mathrm{GC}}\right)+\left(\overrightarrow{\mathrm{GA}\text{'}}+\overrightarrow{\mathrm{GB}\text{'}}+\overrightarrow{\mathrm{GC}\text{'}}\right)$

= $3\overrightarrow{\mathrm{GG}\text{'}}-\left(\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}\right)+\left(\overrightarrow{\mathrm{GA}\text{'}}+\overrightarrow{\mathrm{GB}\text{'}}+\overrightarrow{\mathrm{GC}\text{'}}\right)$

= $3\overrightarrow{\mathrm{GG}\text{'}}+\overrightarrow{0}+\overrightarrow{0}$ = $3\overrightarrow{\mathrm{GG}\text{'}}$

⇒ $\overrightarrow{\text{AA'}}+\overrightarrow{\mathrm{BB}\text{'}}+\overrightarrow{\mathrm{CC}\text{'}}=3\overrightarrow{\mathrm{GG}\text{'}}$ (đpcm).

3.3. Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng

– Điều kiện cần và đủ để hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ ($\overrightarrow{\mathrm{b}}$ ≠ 0) cùng phương là có một số thực k để $\overrightarrow{\mathrm{a}}$ = k$\overrightarrow{\mathrm{b}}$.

– Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để $\overrightarrow{\mathrm{AB}}=\mathrm{k}\overrightarrow{\mathrm{AC}}$.

Nhận xét: Trong mặt phẳng, cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ không cùng phương. Với mỗi vectơ $\overrightarrow{\mathrm{c}}$ có duy nhất cặp số (x; y) thoả mãn $\overrightarrow{\mathrm{c}}=\mathrm{x}\overrightarrow{\mathrm{a}}+\mathrm{y}\overrightarrow{\mathrm{b}}$.

Ví dụ: Cho tam giác ABC. Đặt $\overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{AC}}$. Dựng các điểm M, N sao cho $\overrightarrow{\mathrm{AM}}=\frac{1}{3}\overrightarrow{\mathrm{AB}}$; $\overrightarrow{\mathrm{CN}}=2\overrightarrow{\mathrm{BC}}$.

a) Phân tích $\overrightarrow{\mathrm{CM}}$, $\overrightarrow{\mathrm{AN}}$ theo các vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$.

b) Gọi I là điểm thỏa mãn: $\overrightarrow{\mathrm{MI}}=\overrightarrow{\mathrm{CM}}$. Chứng minh I, A, N thẳng hàng.

Hướng dẫn giải:

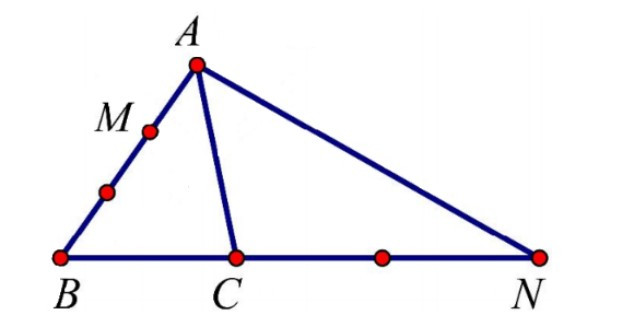
a) Ta có:

+) $\overrightarrow{\mathrm{CM}}$ = $\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AM}}$ = $-\overrightarrow{\mathrm{AC}}+\frac{1}{3}\overrightarrow{\mathrm{AB}}$ = $\frac{1}{3}$$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$.

+) Vì $\overrightarrow{\mathrm{CN}}=2\overrightarrow{\mathrm{BC}}$ ⇒ CN = 2BC ⇒ BC = $\frac{1}{3}$BN ⇒ BN = 3BC.

⇒ $\overrightarrow{\mathrm{BN}}=3\overrightarrow{\mathrm{BC}}$.

⇒ $\overrightarrow{\mathrm{AN}}$ = $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BN}}$ = $\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{BC}}$ = $\overrightarrow{\mathrm{AB}}+3\left(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}\right)$ = $\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{AC}}-3\overrightarrow{\mathrm{AB}}$ 

= $-2\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{AC}}$ = –2$\overrightarrow{\mathrm{a}}$ + 3$\overrightarrow{\mathrm{b}}$.

b) Ta có:

$\overrightarrow{\mathrm{AI}}$ = $\overrightarrow{\mathrm{AM}}+\overrightarrow{\mathrm{MI}}$ = $\frac{1}{3}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CM}}$ = $\frac{1}{3}$$\overrightarrow{\mathrm{a}}$ + $\frac{1}{3}$$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ = $\frac{2}{3}$$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ = $-\frac{1}{3}\left(-2\overrightarrow{a}+3\overrightarrow{b}\right)$

⇒ $\overrightarrow{\mathrm{AI}}$ = $-\frac{1}{3}\overrightarrow{\mathrm{AN}}$.

⇒ I, A, N thẳng hàng.