Với giải Vận dụng trang 62 Toán lớp 7 Chân trời sáng tạo chi tiết trong Chương 3 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Chương 3 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

Vận dụng trang 62 Toán lớp 7: Bạn Nam đã làm một chiếc hộp hình lăng trụ đứng với kích thước như Hình 9. Bạn ấy định sơn các mặt của chiếc hộp, trừ mặt bên dưới. Tính diện tích cần sơn.

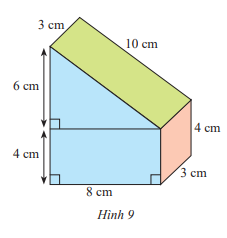
Phương pháp giải:

Lăng trụ đứng có đáy là hình thang.

Bước 1: Tính Sxq = Cđáy . h

Bước 2: Tính Sđáy

Bước 3: Diện tích phần cần sơn = Sxq + Sđáy

Lời giải:

Diện tích xung quanh chiếc hộp là:

 Sxq = Cđáy . h = (6+4+8+4+10).3 = 96 (cm2)

Diện tích đáy là:

Sđáy = (10+4).8 : 2 = 56 (cm2)

Diện tích phần cần sơn là:

96 + 56 = 152 (cm2)

Lý thuyết Diện tích xung quanh và thể tích của một số hình khối trong thực tiễn

Ví dụ: Một tấm lịch để bàn có dạng hình lăng trụ đứng tam giác. Tính diện tích xung quanh của tấm lịch.

Hướng dẫn giải

Diện tích xung quanh của tấm lịch để bàn là:

S_xq = C_đáy . h = (7 + 15 + 15) . 16 = 592 (cm²)

Vậy diện tích xung quanh của tấm lịch là 592 cm².

Ví dụ: Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như hình sau.

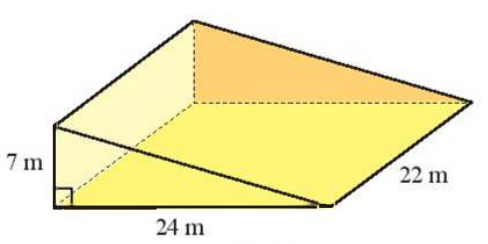
Hãy tính thể tích của khối bê tông.

Hướng dẫn giải

Diện tích đáy của hình lăng trụ đứng tam giác là:

S_đáy = $\frac{1}{2}.7.24$ = 84 (m²).

Thể tích của khối bê tông là:

V = S_đáy . h = 84 . 22 = 1 848 (m³).

Vậy thể tích của khối bê tông là 1 848 m³.

Xem thêm các bài giải Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

HĐ 1 trang 59 Toán lớp 7: Hãy quan sát lăng trụ đứng tam giác (Hình 1) và thực hiện các yêu cầu sau:...

Thực hành 1 trang 59 Toán lớp 7: Tính diện tích xung quanh của hình lăng trụ đứng có đáy là hình thang được cho trong Hình 2...

HĐ 2 trang 60 Toán lớp 7: Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như ở Hình 3b...

Thực hành 2 trang 60 Toán lớp 7: Tính diện tích xung quanh của một cột bê tông hình lăng trụ đứng có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m (Hình 4)...

Thực hành 3 trang 60 Toán lớp 7: Tính thể tích hình lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5...

Thực hành 4 trang 60 Toán lớp 7: Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như Hình 8. Hãy tính thể tích khối bê tông...

Bài 1 trang 62 Toán lớp 7: Một chiếc hộp đèn có dạng hình lăng trụ đứng tam giác có kích thước như Hình 10. Tính diện tích xung quanh của chiếc hộp...

Bài 2 trang 62 Toán lớp 7: Một chiếc lều trại có hình dạng và kích thước như Hình 11. Tính tổng diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) và thể tích của chiếc lều...

Bài 3 trang 62 Toán lớp 7: Một cái bục hình lăng trụ đứng có kích thước như Hình 12...

Bài 4 trang 63 Toán lớp 7: Tính thể tích hình lăng trụ đứng có đáy là hình thang cân với kích thước như hình 13...

Bài 5 trang 63 Toán lớp 7: Để làm đường dẫn bắc ngang một con đê, người ta đúc một khối bê tông có kích thước như Hình 14. Tính chi phí để đúc khối bê tông đó, biết rằng chi phí để đúc 1 m3 bê tông là 1,2 triệu đồng...

Bài 6 trang 63 Toán lớp 7: Một hình lăng trụ đứng tứ giác có kích thước đáy như hình 15, biết chiều cao của lăng trụ là 7 cm. Tính thể tích của hình lăng trụ...

Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

Bài 5: Hoạt động thực hành và trải nghiệm: Các bài toán về đo đạc và gấp hình

Bài tập cuối chương 3

Bài 1: Các góc ở vị trí đặc biệt