Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 7 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác sách Chân trời sáng tạo. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác. Mời các bạn đón xem:

Bài tập Toán lớp 7 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

A. Bài tập Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

A.1. Bài tập trắc nghiệm

Câu 1. Cho lăng trụ đứng tam giác ABC.EGH, biết GH = 4 cm. S_BCHG = 36 cm². Chiều cao của lăng trụ là:

A. 32 cm;

B. 9 cm;

C. 40 cm;

D. 10 cm.

Hướng dẫn giải

Đáp án đúng là: B

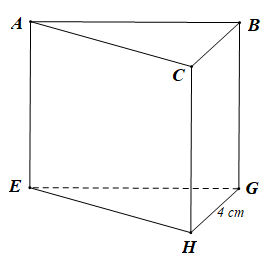
Vì ABC.EGH là lăng trụ đứng tam giác nên mặt bên BCHG là hình chữ nhật.

Do đó S_BCHG = GH. CH = 36 cm²

Mà GH = 4 cm nên CH = S_BCHG : GH = 36 : 4 = 9 (cm).

Chiều cao của hình lăng trụ đứng là độ dài một cạnh bên, mà CH là cạnh bên của hình lăng trụ này.

Vậy chiều cao của lăng trụ đứng ABC.EGH là 9 cm.

Câu 2. Cho hình lăng trụ đứng có đáy là hình vuông, chiều cao bằng 20 cm và diện tích xung quanh bằng 64 cm². Cạnh đáy của hình lăng trụ đứng đó là:

A. 3,2 cm;

B. ± 4 cm;

C. 4 cm;

D. 16 cm.

Hướng dẫn giải

Đáp án đúng là: C

Gọi độ dài cạnh đáy của hình lăng trụ đứng là a (cm) (a > 0).

Diện tích xung quanh của hình lăng trụ đứng đó là:

S_xq = 4 . a²

Do đó 64 = 4 . a²

a² = 16

nên a = 4 hoặc a = –4.

Mà a > 0 nên a = 4 (cm).

Vậy độ dài cạnh đáy của hình lăng trụ đứng đó là 4 cm.

Câu 3. Cho hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ với đáy là hình thoi có độ dài hai đường chéo là 5 cm và 10 cm. Biết thể tích của hình lăng trụ đứng tứ giác là 160 cm³. Chiều cao của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

A. 32 cm;

B. 8 cm;

C. 6,4 cm;

D. 10 cm.

Hướng dẫn giải

Đáp án đúng là: C

Diện tích đáy (hình thoi) của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

$\frac{1}{2}$. 5 . 10 = 25 (cm²)

Chiều cao của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

160 : 25 = 6,4 (cm)

Vậy chiều cao của hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là 6,4 cm.

A.2. Bài tập tự luận

Bài 1. Một chiếc hộp có dạng hình lăng trụ đứng tam giác với các kích thước như hình vẽ sau.

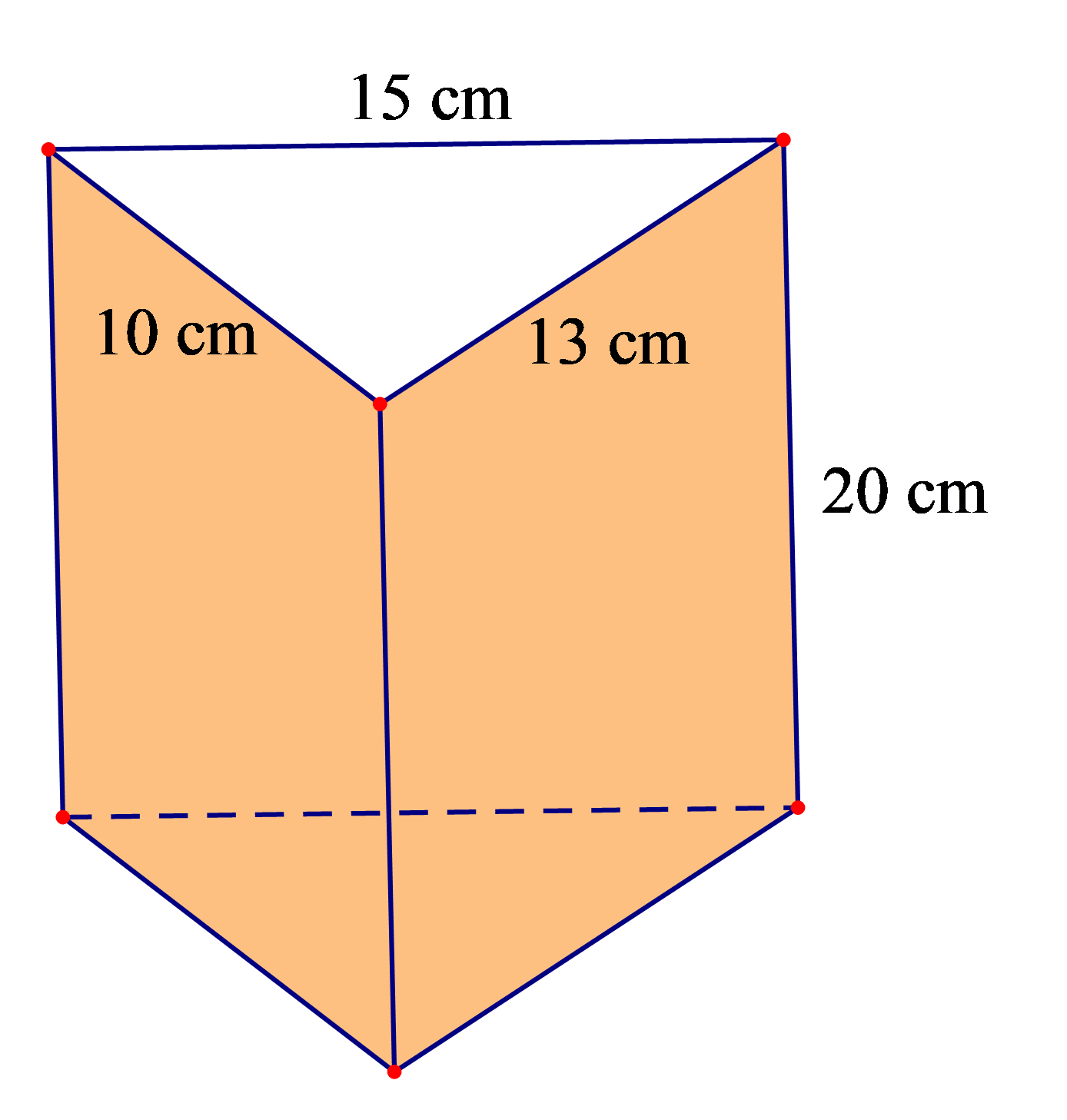
Hãy tính diện tích xung quanh của chiếc hộp.

Hướng dẫn giải

Ta có chu vi đáy của hình lăng trụ đứng tam giác là:

C_đáy = 10 + 13 + 15 = 38 (cm)

Diện tích xung quanh của hình lăng trụ đứng tam giác là:

S_xq = C_đáy . h = 38 . 20 = 760 (cm²).

Vậy diện tích xung quanh của chiếc hộp là 760 cm².

Bài 2. Lòng trong của một chiếc bể chứa nước có dạng hình lăng trụ đứng tứ giác, đáy là hình vuông có cạnh bằng 5 m, chiều cao của bể là 2,5 m. Hỏi bể chứa tối đa được bao nhiêu lít nước.

Hướng dẫn giải

Thể tích nước tối đa bể chứa được bằng thể tích của lòng trong của bể.

Lòng trong của bể hình lăng trụ đứng đáy là hình vuông nên ta có:

S_đáy = 5 . 5 = 25 (m²)

Thể tích lòng trong của bể là:

V = S_đáy . h = 25 . 2,5 = 62,5 (m³) = 62 500 (l).

Vậy bể chứa tối đa được 62 500 lít nước.

Bài 3. Một chiếc hộp đèn có dạng hình lăng trụ đứng tam giác có kích thước như Hình 10. Tính diện tích xung quanh của chiếc hộp.

Hướng dẫn giải

Chu vi đáy của hình lăng trụ đứng tam giác là:

12 + 16 + 20 = 48 (cm)

Diện tích xung quanh của chiếc hộp là:

48 . 25 = 1 200 (cm²)

Vậy diện tích xung quanh của chiếc hộp là 1 200 cm².

Bài 4. Một chiếc lều trại có hình dạng và kích thước như Hình 11. Tính tổng diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) và thể tích của chiếc lều.

Hướng dẫn giải

Chiếc lều trại có hình dạng hình lăng trụ tam giác có đáy là tam giác cân.

Chu vi đáy của hình lăng trụ tam giác là:

2,5 + 2,5 + 4 = 9 (m)

Diện tích xung quanh của hình lăng trụ tam giác là:

9 . 6 = 54 (m²)

Diện tích hai đáy của hình lăng trụ tam giác là:

$2.\frac{1}{2}.4.1,5=6$ (m²)

Diện tích tích tất cả các mặt của hình lăng trụ tam giác là:

54 + 6 = 60 (m²)

Diện tích mặt tiếp giáp với đất là:

6 . 4 = 24 (m²)

Tổng diện tích tấm bạt có thể phủ kín toàn bộ lều bằng tổng diện tích các mặt của hình lăng trụ tam giác trừ diện tích mặt tiếp giáp với đất và bằng:

60 – 24 = 36 (m²)

Diện tích đáy của hình lăng trụ tam giác là:

$\frac{1}{2}.4.1,5=3$ (m²)

Thể tích của chiếc lều là:

3 . 6 = 18 (m³)

Vậy tổng diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) là 36 m² và thể tích của chiếc lều là 18 m³.

Bài 5. Một cái bục hình lăng trụ đứng có kích thước như Hình 12.

a) Người ta muốn sơn tất cả các mặt của cái bục. Diện tích cần phải sơn là bao nhiêu?

b) Tính thể tích của cái bục.

Hướng dẫn giải

Chiếc bục có dạng hình lăng trụ đứng tứ giác.

a) Chu vi đáy của hình lăng trụ đứng tứ giác là:

4 + 8 + 5 + 5 = 22 (dm)

Diện tích xung quanh của hình lăng trụ đứng tứ giác là:

22 . 12 = 264 (dm²).

Diện tích hai đáy của hình lăng trụ đứng tứ giác là:

$2.\frac{5+8}{2}.4=52$ (dm²).

Diện tích tất cả các mặt của hình lăng trụ đứng tứ giác là:

264 + 52 = 316 (dm²).

Diện tích mặt tiếp xúc với mặt đất là:

12 . 8 = 96 (dm²).

Diện tích cần phải sơn của cái bục bằng diện tích tất cả các mặt của hình lăng trụ đứng tứ giác trừ đi diện tích mặt tiếp xúc với mặt đất và bằng:

316 – 96 = 220 (dm²)

Vậy diện tích cần phải sơn của cái bục là 220 dm².

b) Diện tích đáy của hình lăng trụ đứng tứ giác là:

$\frac{5+8}{2}.4=26$ (dm²)

Thể tích của cái bục là:

26 . 12 = 312 (dm³).

Vậy thể tích của cái bục là 312 dm³.

B. Lý thuyết Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

1. Diện tích xung quanh của hình lăng trụ đứng

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao.

S_xq = C_đáy . h

(C_đáy là chu vi đáy, h là chiều cao).

Chú ý: Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng tam giác ABC.DEF sau:

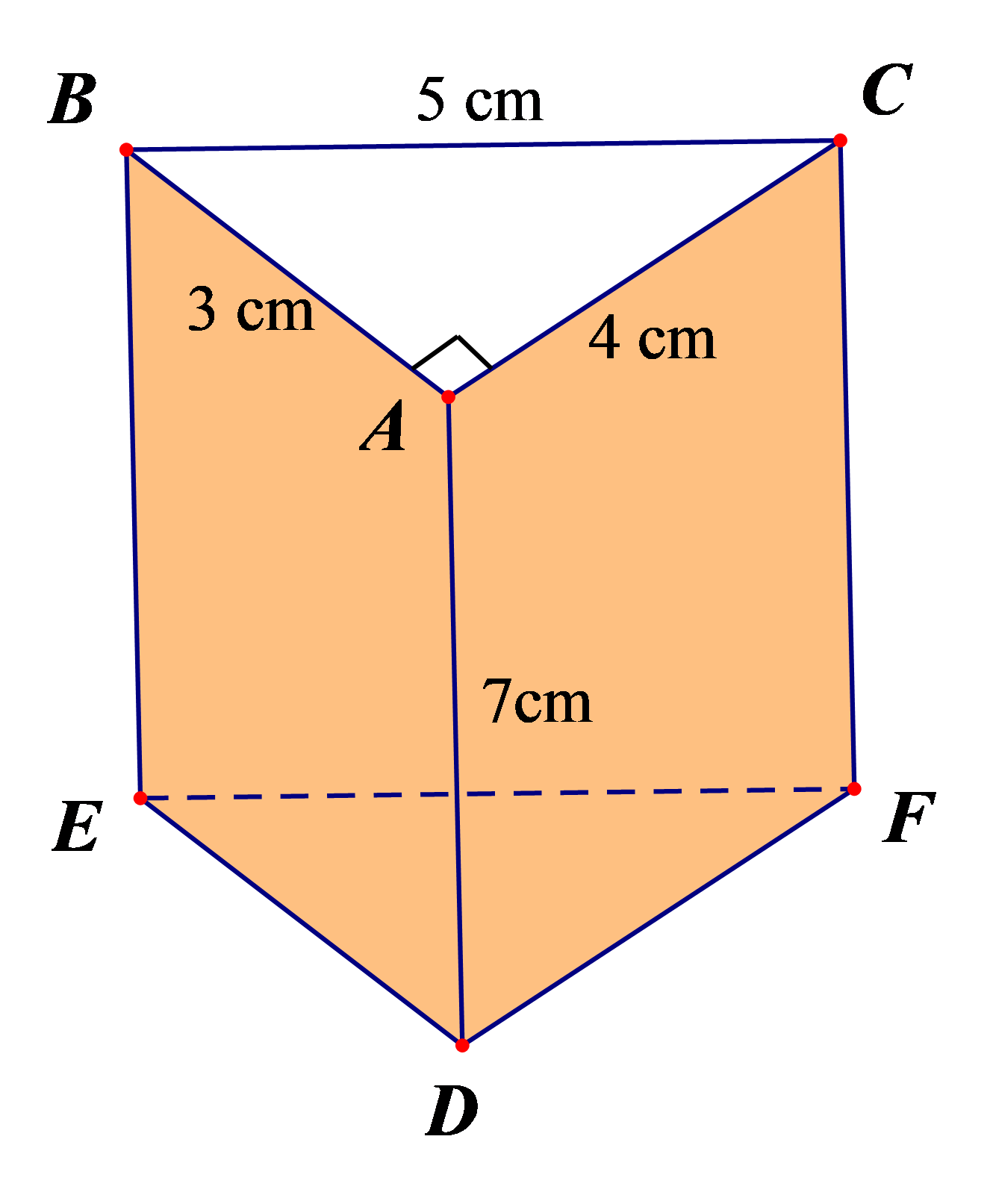
Hướng dẫn giải

Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.DEF là:

S_xq = C_đáy . h = (3 + 4 + 5 ) . 7 = 84 (cm²).

Diện tích một đáy của hình lăng trụ đứng tam giác ABC.DEF là: 

S_đáy =  $\frac{1}{2}.3.4=6$ (cm²)

Diện tích toàn phần của hình lăng trụ đứng tam giác ABC.DEF là:

84 + 2. 6 = 96 (cm²)

Vậy diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng tam giác ABC.DEF lần lượt là 84 cm² và 96 cm².

2. Thể tích của hình lăng trụ đứng

Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.

V = S_đáy . h

(S_đáy là diện tích đáy, h là chiều cao).

Ví dụ: Tính thể tích của hình lăng trụ đứng tứ giác có đáy là hình chữ nhật chiều rộng là 3 cm, chiều dài là 4 cm, và chiều cao của lăng trụ là 5,5 cm.

Hướng dẫn giải

Ta có đáy là hình chữ nhật nên diện tích đáy là:

S_đáy = 3 . 4 = 12 (cm²)

Thể tích của hình lăng trụ đứng tứ giác đó là: 

V = S_đáy . h = 12 . 5,5 = 66 (cm³).

Vậy thể tích của hình lăng trụ đứng tứ giác đó là 66 cm³.

3. Diện tích xung quanh và thể tích của một số hình khối trong thực tiễn

Ví dụ: Một tấm lịch để bàn có dạng hình lăng trụ đứng tam giác. Tính diện tích xung quanh của tấm lịch.

Hướng dẫn giải

Diện tích xung quanh của tấm lịch để bàn là:

S_xq = C_đáy . h = (7 + 15 + 15) . 16 = 592 (cm²)

Vậy diện tích xung quanh của tấm lịch là 592 cm².

Ví dụ: Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như hình sau.

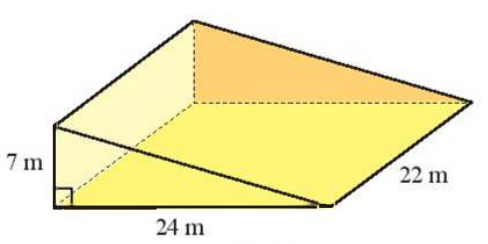
Hãy tính thể tích của khối bê tông.

Hướng dẫn giải

Diện tích đáy của hình lăng trụ đứng tam giác là:

S_đáy = $\frac{1}{2}.7.24$ = 84 (m²).

Thể tích của khối bê tông là:

V = S_đáy . h = 84 . 22 = 1 848 (m³).

Vậy thể tích của khối bê tông là 1 848 m³.