Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 7: Các khái niệm mở đầu chi tiết sách Toán 10 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 7: Các khái niệm mở đầu
Giải Toán 10 trang 46 Tập 1 Kết nối tri thức
Lời giải:
Ta có thể dùng vectơ để biểu diễn vận tốc gió.
Trong đó: hướng của vecto là hướng gió, độ dài vecto biểu thị độ lớn của vận tốc gió.
1. Khái niệm vectơ
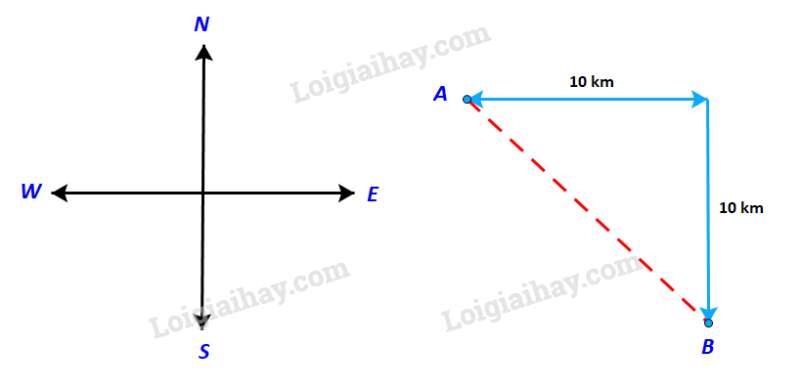
Phương pháp giải:
Xét tam giác, dựa vào độ dài 2 cạnh đã có để suy ra góc A.
Dựa vào định lí Pytago để tính cạnh AB
Từ đó kết luận hướng đi và quãng đường phải đi.
Lời giải:
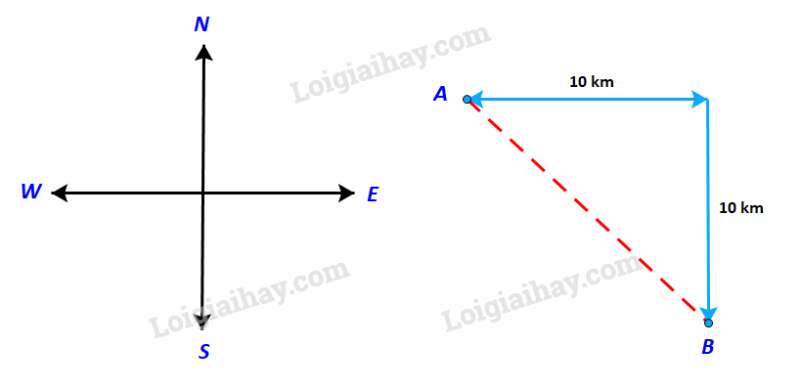
Gọi C là điểm mà tại đó tàu đổi từ hướng đông sang hướng Nam
Xét tam giác ABC ta có:
vuông cân tại C.
Vậy con tàu phải đi theo hướng đông nam, góc so với hướng Đông.
Quãng đường con tàu phải đi là:
Phương pháp giải:
Nhắc lại:
+) Vectơ là một đoạn thẳng có hướng.
+) Độ dài của vectơ là độ dài đoạn thẳng ấy.
Lời giải:
Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
Chú ý khi giải:
Vectơ khác vectơ (khác nhau điểm đầu và điểm cuối).
2. Hai vectơ cùng phương, cùng hướng, bằng nhau
a) Các làn đường song song với nhau.
b) Các xe chạy theo cùng một hướng
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau.
Phương pháp giải:
Quan sát làn đường và hướng đi chuyển (mũi tên) của các xe.
Lời giải:
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.
Giải Toán 10 trang 48 Tập 1 Kết nối tri thức
Phương pháp giải:
Quan sát hai vectơ cùng hướng, ngược hướng chỉ ra các đặc điểm về giá và hướng (chiều) của các vectơ đó.
Lời giải:
Hai vectơ và cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ và ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ có giá song song với giá của vectơ , ngược hướng với vectơ nên hai vectơ và ngược hướng với nhau.
Vectơ có giá song song với giá của vectơ , cùng hướng với vectơ nên hai vectơ và cùng hướng với nhau.
Vectơ có giá không song song với giá của vectơ nên hai vectơ và không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
Giải Toán 10 trang 49 Tập 1 Kết nối tri thức
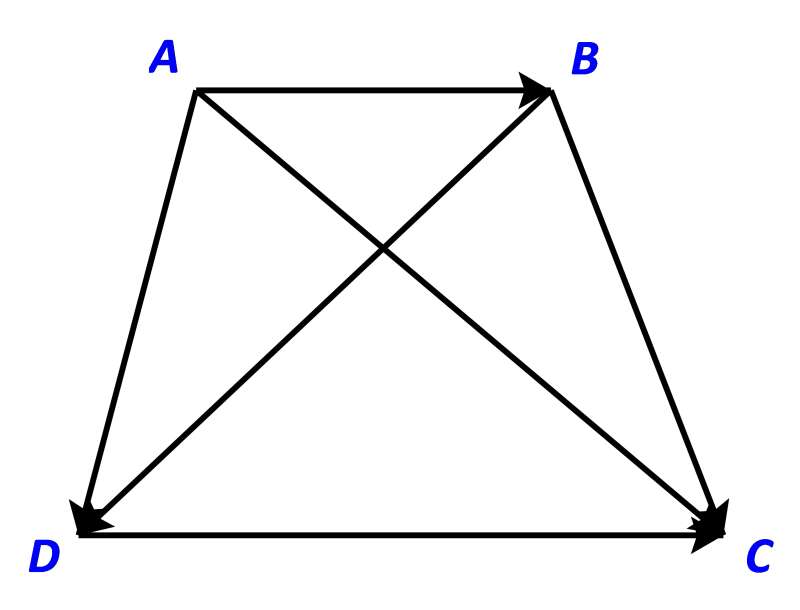
Phương pháp giải:
Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng
(Cùng hướng tức là giá của chúng song song và cùng chiều với nhau)
Lời giải:
Dễ thấy:
nhưng và không song song với nhau. Do đó hai vectơ và không bằng nhau.
do đó hai vectơ và không bằng nhau.
và không song song với nhau. Do đó hai vectơ và không bằng nhau.
a) và ngược hướng
b) và cùng phương
c) và cùng hướng
d) và ngược hướng
Phương pháp giải:
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương mà cùng chiều thì được gọi là cùng hướng.
Hai vectơ cùng phương mà ngược chiều thì được gọi là ngược hướng.
Nhận xét: các cặp vectơ đều có cùng điểm đầu nên giá của chung song song khi và chỉ khi 3 điểm đó thẳng hàng.
Lời giải:
a) và ngược hướng

A, B, thẳng hàng và A nằm giữa B và M
b) và cùng phương
TH1:
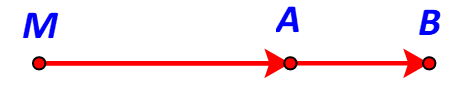
M, A, B thẳng hàng & A nằm giữa M và B.
TH2:

M, A, B thẳng hàng & B nằm giữa M và A.
c) và cùng hướng
TH1:

A, M, B thẳng hàng & M nằm giữa A và B.
TH2:

A, M, B thẳng hàng & B nằm giữa A và M.
d) và ngược hướng

A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) và ngược hướng
Giải Toán 10 trang 50 Tập 1 Kết nối tri thức
a) Hãy thể hiện trên hình vẽ, vectơ vận tốc của dòng nước và các vectơ vận tốc thực tế của các ca nô A, B. ?
b) Trong các vectơ , những cặp vectơ nào cùng phương và những cặp vectơ nào ngược hướng?
Phương pháp giải:
Vẽ 3 vectơ, lần lượt mô phỏng .
Nhận xét về phương và chiều của chúng để kết luận cùng hướng hay ngược hướng.
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương mà cùng chiều thì được gọi là cùng hướng.
Hai vectơ cùng phương mà ngược chiều thì được gọi là ngược hướng.
Lời giải:
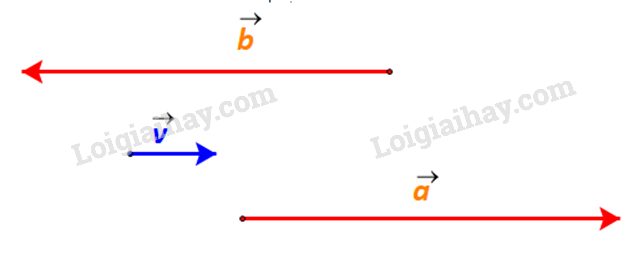
Gọi lần lượt là vectơ vận tốc riêng của ca nô A và B (cùng độ lớn).
Vì ca no A chạy xuôi dòng nên ngoài vận tốc riêng của ca nô, ca nô A còn được đẩy đi bởi vận tốc của dòng nước. Do đó vectơ vận tốc thực của cano A cùng hướng với vectơ và có độ lớn bằng tổng của vận tốc riêng và vận tốc dòng nước, là 18 km/h.
Ngược lại, ca nô đi ngược dòng nên bị cản lại một phần bởi dòng nước. Vì vận tốc của dòng nước nhỏ hơn vận tốc riêng của cano B nên vectơ vận tốc thực của cano B cùng hướng với vectơ và có độ lớn bằng hiệu giữa vận tốc riêng và vận tốc dòng nước, là 12 km/h.
Ta biểu diễn vận tốc thực của ca nô A và ca nô B như sau:
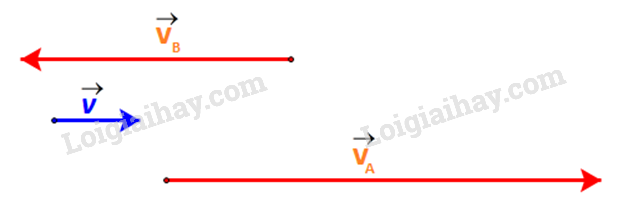
b) Dễ thấy:
Các vectơ đều có giá song song nên chúng cùng phương với nhau.
Ca nô A đi xuôi dòng nên vectơ vận tốc thực của ca nô A cùng hướng với vectơ vận tốc dòng nước.
Hay và cùng hướng.
Ca nô A đi ngược dòng nên vectơ vận tốc thực của ca nô B ngược hướng với vectơ vận tốc dòng nước.
Hay và ngược hướng.
Chú ý khi giải
Vận tốc riêng của cano là vận tốc của cano khi dòng nước đứng im.
Vận tốc thực của cano là vận tốc của cano khi kết hợp với dòng nước (đang chảy)
Bài tập
Bài 4.1 trang 50 Toán lớp 10: Cho 3 vectơ đều khác . Những khẳng định nào sau đây là đúng?
a) đều cùng hướng với vectơ ;
b) Nếu không cùng hướng với thì ngược hướng với .
c) Nếu và đều cùng phương với thì và cùng phương.
d) Nếu và đều cùng hướng với thì và cùng hướng.
Phương pháp giải:
Vectơ cùng hướng, cùng phương với mọi vectơ.
Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương.
Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
Lời giải:
a) Đúng vì vectơ cùng hướng với mọi vectơ.
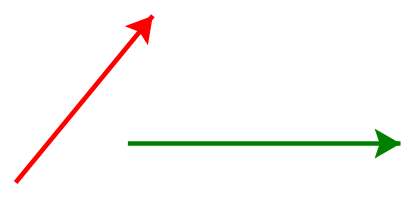
b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).
c) Đúng.
và đều cùng phương với thì a // c và b // c do đó a // b tức là và cùng phương.
d) Đúng.
và đều cùng hướng với thì và cùng phương , cùng chiều đo đó cùng hướng.
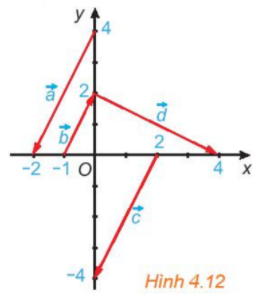
Phương pháp giải:
Hai vectơ cùng phương là hai vectơ có giá song song hoặc trùng nhau.
Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
Lời giải:
Các vecto cùng phương là:
Trong đó cặp vecto cùng hướng, cặp vecto và cặp vecto ngược hướng.
Bài 4.3 trang 50 Toán lớp 10: Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi
Lời giải:
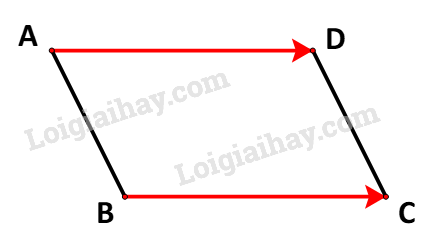
Tứ giác ABCD là một hình bình hành
Hai vecto và cùng hướng và AD = BC.
(đpcm)
Phương pháp giải:
Chỉ ra các vecto (tạo bởi 5 điểm A; B; C; D; O) bằng nhau.
Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải:
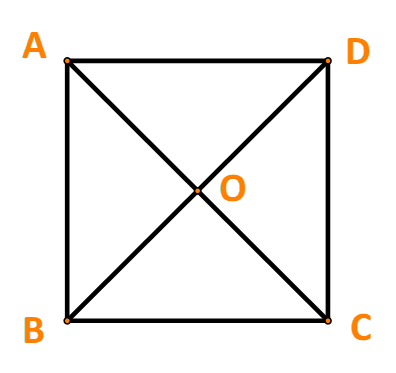
Tập hợp S là:
Các nhóm trong S là:
a) Chỉ ra mỗi quan hệ giữa hai vecto trên.
b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn vởi vecto . Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?
Phương pháp giải:
+) Tọa độ của vecto là
+) Tọa độ của vecto là
Lời giải:
a) Tọa độ của vecto là , vecto là
b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.
Vì nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.
Lý thuyết Các khái niệm mở đầu
1. Khái niệm vectơ
– Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.
– Độ dài vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Chú ý:
+ Vectơ có điểm đầu A và điểm cuối B được kí hiệu là , đọc là vectơ AB.
+ Để vẽ một vectơ, ta vẽ đoạn thẳng nối điểm đầu và điểm cuối của nó, rồi đánh dấu mũi tên ở điểm cuối.
+ Vectơ còn được kí hiệu là , , , ,…
+ Độ dài của vectơ , tương ứng được kí hiệu là , .
Ví dụ: Cho hình vuông ABCD với cạnh có độ dài bằng 1. Tính độ dài vectơ , .
Hướng dẫn giải
Vì ABCD là hình vuông nên .
Áp dụng định lý Pythagore cho tam giác ABD vuông tại A, có các cạnh góc vuông AB = AD = 1.
Ta có: BD2 = AB2 + AD2.
Suy ra: BD2 = 12 + 12 = 2 ⇒ BD = .
Do đó = BD =
Mặt khác Vì ABCD là hình vuông nên hai đường chéo BD và AC bằng nhau.
Vì vậy AC = BD =
Do đó: = AC = ;
Vậy = ; =
2. Hai vectơ cùng phương, cùng hướng, bằng nhau.
+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
+ Hai vectơ và được gọi là bằng nhau, kí hiệu là = , nếu chúng có cùng độ dài và cùng hướng.
Ví dụ:
Trong hình trên đường thẳng m đi qua điểm đầu và điểm cuối của vectơ , nên đường thẳng m gọi là giá của vectơ .
Tương tự, đường thẳng n là giá của hai vectơ và .
Đường thẳng m và n song song với nhau nên ba vectơ và và là các vectơ cùng phương.
và cùng phương nhưng ngược hướng; và cùng phương vàcùng hướng.
Hai vectơ và cùng hướng, ngoài ra chúng có độ dài bằng nhau nên = .
Chú ý:
+ Ta cũng xét các vectơ điểm đầu và điểm cuối trùng nhau (chẳng hạn , ), gọi là các vectơ–không.
+ Ta quy ước vectơ–không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.
+ Các vectơ–không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là .
+ Với mỗi điểm O và vectơ cho trước, có duy nhất điểm A sao cho .
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi và cùng phương.
Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.
Ví dụ: Một vật A thả chìm hoàn toàn dưới đáy một cốc chất lỏng. Khi đó biểu diễn lực đẩy Ác–si–mét và biểu diễn trọng lực tác dụng lên vật A.
và tác dụng lên vật A theo phương thẳng đứng, hai lực này cùng phương nhưng ngược hướng. Do vật chìm hoàn toàn dưới đáy cốc nên trọng lực có độ lớn lớn hơn lực đẩy Ác–si–mét , cụ thể .
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 8: Tổng và hiệu của hai vectơ