+ Tìm căn bậc hai số học của a:

$\sqrt{a}=b$ sao cho $b^2=a;b\ge 0$

+ $\sqrt{a}=b$thì $a=b^2$

$\begin{array}{l}a)\sqrt{0,49}+\sqrt{0,64};b)\sqrt{0,36}-\sqrt{0,81};\\ c)8.\sqrt{9}-\sqrt{64};d)0,1.\sqrt{400}+0,2.\sqrt{1600}\end{array}$

Phương pháp giải:

$\sqrt{a}=b$ sao cho $b^2=a;b\ge 0$

Lời giải:

$\begin{array}{l}a)\sqrt{0,49}+\sqrt{0,64}=0,7+0,8=1,5;\\ b)\sqrt{0,36}-\sqrt{0,81}=0,6-0,9=-0,3;\\ c)8.\sqrt{9}-\sqrt{64}=8.3-8=24-8=16;\\ d)0,1.\sqrt{400}+0,2.\sqrt{1600}=0,1.20+0,2.40=2+8=10\end{array}$

a) Tính diện tích của hình vuông ABCD.

b) Tính độ dài đường chéo AB.

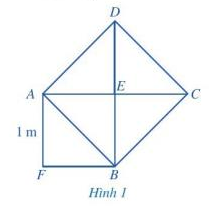
Phương pháp giải:

a) $S_{ABCD}=4.S_{AEB}$

b) Cạnh x của hình vuông có diện tích S là: $x=\sqrt{S}$

Lời giải:

a) Ta có: $S_{ABCD}=4.S_{AEB}$ = 4. $\frac{1}{2}.1.1$ = 2 (dm2)

b) AB = $\sqrt{S{}_{ABCD}}=\sqrt{2}$ (dm)

Lý thuyết Số vô tỉ. Căn bậc hai số học

1. Số vô tỉ

1.1 Khái niệm số vô tỉ

Trong đời sống thực tiễn của con người, ta thường gặp những số không phải là số hữu tỉ. Những số không phải là số hữu tỉ được gọi là số vô tỉ.

Ví dụ: Số Pi (π) là tỉ số giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó và là một số vô tỉ.

1.2 Số thập phân vô hạn không tuần hoàn

Những số thập phân vô hạn mà phần thập phân của nó không có một chu kì nào cả, những số đó được gọi là số thập phân vô hạn không tuần hoàn.

Ví dụ:

Số –1,359130000110578… là số thập phân vô hạn không tuần hoàn.

Số π = 3,14159265358979323846264338… là số thập phân vô hạn không tuần hoàn.

1.3 Biểu diễn thập phân của số vô tỉ

Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.

Ví dụ:

Số –1,359130000110578… là số vô tỉ.

Số π = 3,14159265358979323846264338… là số vô tỉ.

- Nếu a là một số tự nhiên, số nguyên hay số hữu tỉ thì a không thể là số vô tỉ.

2. Căn bậc hai số học

- Căn bậc hai số học của một số a không âm là số x không âm sao cho x² = a.

- Căn bậc hai số học của số a (a ≥ 0) được kí hiệu là $\sqrt{\mathrm{a}}$.

- Căn bậc hai số học của số 0 là số 0, viết là: $\sqrt{0}=0$.

Chú ý: Cho a ≥ 0. Khi đó: 

+  Đẳng thức $\sqrt{\mathrm{a}}$ = b là đúng nếu b ≥ 0 và b² = a.

+  ${\left(\sqrt{\mathrm{a}}\right)}^2=\mathrm{a}$.

Ví dụ:

- Ta có 9 > 0 và 9² = 81 nên 9 là căn bậc hai số học của 81. Ta viết: $\sqrt{81}=9$.

- Ta có 0,4 ≥ 0 và (0,4)² = 0,16 nên 0,4 là căn bậc hai số học của 0,16.

Ta viết $\sqrt{0,16}=0,4$.

- Ta có (– 5)² = 25 nhưng – 5 < 0 nên – 5 không phải căn bậc hai số học của số 25.

Nhận xét:

- Nếu số nguyên dương a không phải là bình phương của bất kì số nguyên dương nào thì  $\sqrt{\mathrm{a}}$ là số vô tỉ.

Ví dụ: $\sqrt{2};\sqrt{3};\sqrt{5};\sqrt{6};\sqrt{7};\mathrm{...}$ đều là các số vô tỉ.

- Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay.

Ví dụ: Để tính $\sqrt{3}$ và $\sqrt{256.36}$ bằng máy tính cầm tay ta làm như sau:

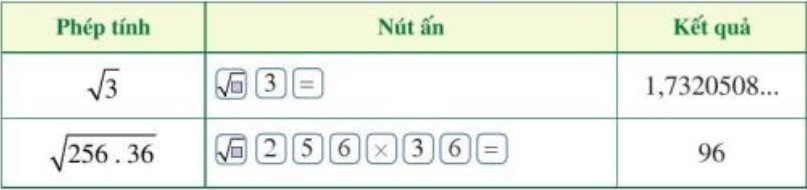
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Bài tập cuối chương 1

Bài 2: Tập hợp R các số thực

Bài 3: Giá trị tuyệt đối của một số thực

Bài 4: Làm tròn và ước lượng