Giải SGK Toán 7 (Cánh diều) Bài tập cuối chương 1

Nguyễn Thị Hằng Ngày: 26-08-2024 Lớp 7

15.3 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối chương 1 chi tiết sách Toán 7 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài tập cuối chương 1

Video bài giảng Bài tập cuối chương 1 - Cánh diều

Giải Toán 7 trang 30 Tập 1

Bài 1 trang 30 toán lớp 7: a) Sắp xếp các số sau theo thứ tự tăng dần: 0, $5; 1; \frac{- 2}{3}$ .

b) Trong ba điểm A, B, C trên trục số dưới đây có một điểm biểu diễn số hữu tỉ 0,5. Hãy xác định điểm đó.

Bài 1 trang 30 toán lớp 7 Tập 1 | Cánh diều (ảnh 1)

Phương pháp giải:

a) So sánh các số rồi sắp xếp theo thứ tự tăng dần.

b) Số 0,5 nằm giữa số 0 và số 1.

Lời giải:

a) Ta có $\frac{- 2}{3} < 0, 5 < 1$ nên:

Sắp xếp các số đã cho theo thứ tự tăng dần là: $\frac{- 2}{3}; 0, 5; 1$

b) Số 0,5 nằm giữa số 0 và số 1

=> Điểm B biểu diễn số hữu tỉ 0,5.

Bài 2 trang 30 Toán lớp 7: Tính:

a) $5 \frac{3}{4} . \frac{- 8}{9}$ ; b) $3 \frac{3}{4} : 2 \frac{1}{2}$ c) $\frac{- 9}{5} : \frac{1}{2}$ d) ${(1, 7)}^{2023} : {(1, 7)}^{2021}$ .

Phương pháp giải:

Quy các phép tính về thực hiện phép chia hai phân số, chia hai lũy thừa cùng cơ số.

Lời giải:

a) $5 \frac{3}{4} . \frac{- 8}{9} = \frac{23}{4} . \frac{- 8}{9} = \frac{- 46}{9}$ ;

b) $3 \frac{3}{4} : 2 \frac{1}{2} = \frac{15}{4} : \frac{5}{2} = \frac{15}{4} . \frac{2}{5} = \frac{3}{2}$

c) $\frac{- 9}{5} : \frac{1}{2} = \frac{- 9}{5} .2 = \frac{- 18}{5}$

d) ${(1, 7)}^{2023} : {(1, 7)}^{2021} = {(1, 7)}^{2023 - 2021} = {(1, 7)}^{2} = 2, 89$ .

Bài 3 trang 30 Toán lớp 7: Tính một cách hợp lí:

a) $\frac{- 5}{12} + (- 3, 7) - \frac{7}{12} - 6, 3$ ; b) $2, 8. \frac{- 6}{13} - 7, 2 - 2, 8. \frac{7}{13}$

Phương pháp giải:

a)Nhóm các phân số với nhau, các số thập phân với nhau rồi thực hiện phép tính.

b)Áp dụng tính chất phân phối của phép nhân với phép trừ: a.b-a.c=a.(b-c)

Lời giải:

$\begin{array}{l} \frac{- 5}{12} + (- 3, 7) - \frac{7}{12} - 6, 3 \\ = (\frac{- 5}{12} - \frac{7}{12}) - (3, 7 + 6, 3) \\ = - 1 - 10 = - 11 \end{array}$

$\begin{array}{l} 2, 8. \frac{- 6}{13} - 7, 2 - 2, 8. \frac{7}{13} \\ = 2, 8. (\frac{- 6}{13} - \frac{7}{13}) - 7, 2 \\ = 2, 8. (- 1) - 7, 2 \\ = - 2, 8 - 7, 2 = - 10 \end{array}$

Bài 4 trang 30 Toán lớp 7: Tính:

a) $0, 3 - \frac{4}{9} : \frac{4}{3} \cdot \frac{6}{5} + 1$ ;

b) ${(\frac{- 1}{3})}^{2} - \frac{3}{8} : (0, 5)^{3} - \frac{5}{2} \cdot (- 4)$ ;

c) $1 + 2 : (\frac{2}{3} - \frac{1}{6}) \cdot (- 2, 25)$

d) $[(\frac{1}{4} - 0, 5) \cdot 2 + \frac{8}{3}] : 2$ .

Phương pháp giải:

Thực hiện phép tính theo thứ tự:

+ Ngoặc: ( ) => [ ]

+ Phép tính: Lũy thừa => Nhân, chia => Cộng, trừ.

Lời giải:

$\begin{array}{l} 0, 3 - \frac{4}{9} : \frac{4}{3} \cdot \frac{6}{5} + 1 \\ = \frac{3}{10} - \frac{4}{9} . \frac{3}{4} . \frac{6}{5} + 1 \\ = \frac{3}{10} - \frac{2}{5} + 1 \\ = \frac{3}{10} - \frac{4}{10} + \frac{10}{10} \\ = \frac{9}{10} \end{array}$

$\begin{array}{l} {(\frac{- 1}{3})}^{2} - \frac{3}{8} : (0, 5)^{3} - \frac{5}{2} \cdot (- 4) \\ = \frac{1}{9} - \frac{3}{8} : \frac{1}{8} - \frac{5}{2} . (- 4) \\ = \frac{1}{9} - 3 + 10 \\ = \frac{1}{9} - \frac{27}{9} + \frac{90}{9} \\ = \frac{64}{9} \end{array}$

$\begin{array}{l} 1 + 2 : (\frac{2}{3} - \frac{1}{6}) \cdot (- 2, 25) \\ = 1 + 2 : (\frac{4}{6} - \frac{1}{6}) \cdot (- \frac{9}{4}) \\ = 1 + 2 : \frac{1}{2} . (- \frac{9}{4}) \\ = 1 + 2. \frac{2}{1} . (- \frac{9}{4}) \\ = 1 + (- 9) = - 8 \end{array}$ $\begin{array}{l} 1 + 2 : (\frac{2}{3} - \frac{1}{6}) \cdot (- 2, 25) \\ = 1 + 2 : (\frac{4}{6} - \frac{1}{6}) \cdot (- \frac{9}{4}) \\ = 1 + 2 : \frac{1}{2} . (- \frac{9}{4}) \\ = 1 + 2. \frac{2}{1} . (- \frac{9}{4}) \\ = 1 + (- 9) = - 8 \end{array}$

$\begin{array}{l} [(\frac{1}{4} - 0, 5) \cdot 2 + \frac{8}{3}] : 2 \\ = [(\frac{1}{4} - \frac{2}{4}) \cdot 2 + \frac{8}{3}] . \frac{1}{2} \\ = (\frac{- 1}{4} .2 + \frac{8}{3}) . \frac{1}{2} \\ = (\frac{- 1}{2} + \frac{8}{3}) . \frac{1}{2} \\ = \frac{13}{6} . \frac{1}{2} = \frac{13}{12} \end{array}$ .

Bài 5 trang 30 Toán lớp 7: Tìm x, biết:

a) $x + (- \frac{2}{9}) = \frac{- 7}{12}$ ;

b) $(- 0, 1) - x = \frac{- 7}{6}$

c) $(- 0, 12) \cdot (x - \frac{9}{10}) = - 1, 2$ ;

d) $(x - \frac{3}{5}) : \frac{- 1}{3} = 0, 4.$

Phương pháp giải:

- Áp dụng quy tắc chuyển vế và đổi dấu ở ý a và ý b.

- Ý c: Muốn tìm thừa số ta lấy thương chia cho thừa số còn lại sau đó áp dụng quy tắc chuyển vế đổi dấu.

- Ý d: Muốn tìm số bị chia ta lấy thương nhân với số chia sau đó áp dụng quy tắc chuyển vế đổi dấu.

Lời giải:

$\begin{array}{l} x + (- \frac{2}{9}) = \frac{- 7}{12} \\ x = \frac{- 7}{12} + \frac{2}{9} \\ x = \frac{- 21}{36} + \frac{8}{36} \\ x = \frac{- 13}{26} \end{array}$

Vậy $x = \frac{- 13}{26}$ .

$\begin{array}{l} (- 0, 1) - x = \frac{- 7}{6} \\ \frac{- 1}{10} - x = \frac{- 7}{6} \\ x = \frac{- 1}{10} + \frac{7}{6} \\ x = \frac{- 3}{30} + \frac{35}{30} \\ x = \frac{32}{30} \\ x = \frac{16}{15} \end{array}$

Vậy $x = \frac{16}{15}$

$\begin{array}{l} (- 0, 12) \cdot (x - \frac{9}{10}) = - 1, 2 \\ \frac{- 3}{25} \cdot (x - \frac{9}{10}) = \frac{- 6}{5} \\ x - \frac{9}{10} = \frac{- 6}{5} : (\frac{- 3}{25}) \\ x - \frac{9}{10} = \frac{- 6}{5} . \frac{- 25}{3} \\ x - \frac{9}{10} = 10 \\ x = 10 + \frac{9}{10} \\ x = \frac{109}{10} \end{array}$

Vậy $x = \frac{109}{10}$ .

$\begin{array}{l} (x - \frac{3}{5}) : \frac{- 1}{3} = 0, 4 \\ (x - \frac{3}{5}) : \frac{- 1}{3} = \frac{2}{5} \\ x - \frac{3}{5} = \frac{2}{5} . \frac{- 1}{3} \\ x - \frac{3}{5} = \frac{- 2}{15} \\ x = \frac{- 2}{15} + \frac{3}{5} \\ x = \frac{7}{15} \end{array}$

Vậy $x = \frac{7}{15}$ .

Bài 6 trang 30 Toán lớp 7: Sắp xếp các số sau theo thứ tự tăng dần:

a) $(0, 2)^{0}; (0, 2)^{3}; (0, 2)^{1}; (0, 2)^{2};$

b) $(- 1, 1)^{2}; (- 1, 1)^{0}; (- 1, 1)^{1}; (- 1, 1)^{3}$ .

Phương pháp giải:

Tính các lũy thừa và so sánh

Lời giải:

a) ${(0, 2)}^{0} = 1; {(0, 2)}^{1} = 0, 2; {(0, 2)}^{2} = 0, 04; {(0, 2)}^{3} = 0, 008$

Vì 0,008 < 0, 04 < 0,2< 1 nên sắp xếp các số theo thứ tự tăng dần là:

$(0, 2)^{0}; (0, 2)^{1}; (0, 2)^{2}; (0, 2)^{3} .$

b) ${(- 1, 1)}^{0} = 1; {(- 1, 1)}^{1} = - 1, 1; {(- 1, 1)}^{2} = 1, 21; {(- 1, 1)}^{3} = - 1, 331$

Vì -1,331 < -1,1 < 1 < 1,21 nên sắp xếp các số theo thứ tự tăng dần là:

$(- 1, 1)^{3}; (- 1, 1)^{1} (- 1, 1)^{0}; (- 1, 1)^{2}$

Chú ý:

- Nếu phần cơ số lớn hơn 1 thì khi số mũ tăng giá trị lũy thừa tăng

- Nếu phần cơ số lớn hơn 0, nhỏ hơn 1 thì khi số mũ tăng giá trị lũy thừa giảm

Bài 7 trang 30 Toán lớp 7: Trọng lượng của một vật thể trên Mặt Trăng bằng khoảng $\frac{1}{6}$ trọng lượng của nó trên Trái Đất. Biết trọng lượng của một vật trên Trái Đất được tính theo công thức: $P = 10 m$ với $P$ là trọng lượng của vật tính theo đơn vị Niu-tơn (kí hiệu $N$ ); $m$ là khối lượng của vật tính theo đơn vị ki-lô-gam.

(Nguồn: Khoa học tự nhiên 6, NXB Đại học Sư phạm, 2021)

Nếu trên Trái Đất một nhà du hành vũ trụ có khối lượng là $75, 5 k g$ thì trọng lượng của người đó trên Mặt Trăng sẽ là bao nhiêu Niu-tơn (làm tròn kết quả đến hàng phần trăm)?

Phương pháp giải:

- Trọng lượng người đó trên mặt trăng = Trọng lượng người đó trên Trái Đất . $\frac{1}{6}$

- Đổi đơn vị tính trọng lượng sang Niu-tơn.

Lời giải:

Trọng lượng người đó trên Mặt Trăng là: $75, 5. \frac{1}{6} = \frac{151}{12}$ (kg)

Trọng lượng người đó trên Mặt Trăng tính bằng đơn vị Niu-tơn là:

$\frac{151}{12} .10 \approx 125, 83$ (N)

Giải Toán 7 trang 31 Tập 1

Bài 8 trang 31 Toán lớp 7: Một người đi quãng đường từ địa điểm $A$ đến địa điểm $B$ với vận tốc $36 k m / h$ mất 3,5 giờ. Từ địa điểm $B$ quay trở về địa điểm $A$ , người đó đi với vận tốc $30 k m / h$ . Tính thời gian đi từ địa điểm $B$ quay trở về địa điểm $A$ của người đó.

Phương pháp giải:

Áp dụng công thức: quãng

đường = vận tốc . thời gian

Tính quãng đường AB

⇨ Thời gian người đi quãng đường từ địa điểm B đến địa điểm A

Lời giải:

Quãng đường AB dài: $36.3, 5 = 126$ (km)

Thời gian người đó đi quãng đường từ địa điểm B về địa điểm A là:

$126 : 30 = 4, 2$ (giờ)

Bài 9 trang 31 Toán lớp 7: Một trường trung học cơ sở có các lớp 7A, 7B, 7C, 7D, 7E; mỗi lớp đều có 40 học sinh. Sau khi sơ kết Học kì I, số học sinh đạt kết quả học tập ở mức Tót của mỗi lớp đó được thể hiện qua biểu đồ cột ở Hình 9.

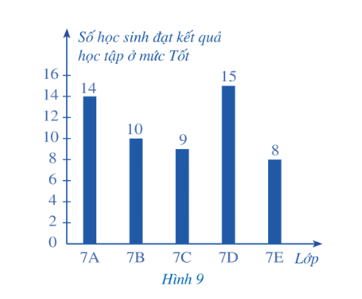
Toán lớp 7 Bài tập cuối chương 1 | Cánh diều (ảnh 1)

a) Lớp nào có số học sinh đạt kết quả học tập ở mức Tốt ít hơn một phần tư số học sinh của cả lớp?

b) Lớp nào có số học sinh đạt kết quả học tập ở mức Tốt nhiều hơn một phần ba số học sinh của cả lớp?

c) Lớp nào có tỉ lệ học sinh đạt kết quả học tập ở mức Tốt cao nhất, thấp nhất?

Phương pháp giải:

- Tính một phần ba và một phần tư số học sinh của cả lớp

- Quan sát biểu đồ và trả lời câu hỏi.

Lời giải:

a) Một phần tư số học sinh cả lớp là: $\frac{1}{4} .40 = 10$ (học sinh).

=>Lớp 7C và 7E có số học sinh đạt kết quả học tập ở mức Tốt ít hơn một phần tư số học sinh của cả lớp.

b) Một phần ba số học sinh cả lớp là: $\frac{1}{3} .40 \approx 13$ (học sinh).

=> Lớp 7A và 7D có số học sinh đạt kết quả học tập ở mức Tốt nhiều hơn một phần ba số học sinh của cả lớp.

c) Lớp 7D có tỉ lệ học sinh đạt kết quả học tập ở mức Tốt cao nhất.

Lớp 7E có tỉ lệ học sinh đạt kết quả học tập ở mức Tốt thấp nhất.

Bài 10 trang 31 Toán lớp 7: Sản lượng chè và hạt tiêu xuất khẩu của Việt Nam qua một số năm được biểu diễn trong biểu đồ cột kép ở Hình 10.

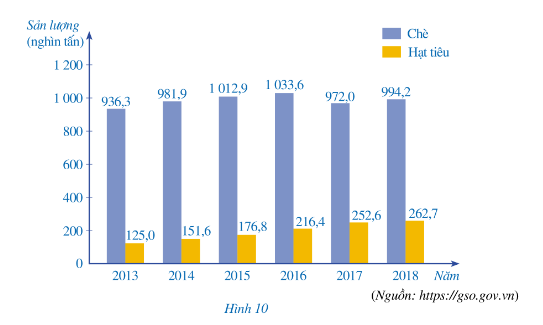
a) Những năm nào Việt Nam có sản lượng chè xuất khẩu trên 1 triệu tấn? Sản lượng hạt tiêu xuất khẩu trên 0,2 triệu tấn?

b) Năm nào Việt Nam có sản lượng chè xuất khẩu lớn nhất? Sản lượng hạt tiêu xuất khẩu lớn nhất?

c) Tính tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018 (làm tròn kết quả đến hàng đơn vị)

Toán lớp 7 Bài tập cuối chương 1 | Cánh diều (ảnh 2) Phương pháp giải:

- Quan sát biểu đồ và trả lời câu hỏi.

- Tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018 = sản lượng chè xuất khẩu năm 2013 : sản lượng chè xuất khẩu năm 2018.100%

Lời giải:

Dựa vào Hình 10, sản lượng chè xuất khẩu của Việt Nam ở các năm 2013, năm 2014, năm 2015, năm 2016, năm 2017, năm 2018 lần lượt là 936,3 nghìn tấn; 981,9 nghìn tấn; 1012,9 nghìn tấn; 1 033,6 nghìn tấn; 972,0 nghìn tấn; 994,2 nghìn tấn.

Sản lượng hạt tiêu xuất khẩu của Việt Nam ở các năm 2013, năm 2014, năm 2015, năm 2016, năm 2017, năm 2018 lần lượt là 125,0 nghìn tấn; 151,6 nghìn tấn; 176,8 nghìn tấn; 216,4 nghìn tấn; 252,6 nghìn tấn; 262,7 nghìn tấn.

a) Năm 2015 và năm 2016 sản lượng chè xuất khẩu trên 1 triệu tấn.

Năm 2016, 2017, 2018 sản lượng hạt tiêu xuất khẩu trên 0,2 triệu tấn.

b) Năm 2016 Việt Nam có sản lượng chè xuất khẩu lớn nhất.

Năm 2018 Việt Nam sản lượng hạt tiêu xuất khẩu lớn nhất.

c) Tỉ số phần trăm của sản lượng chè xuất khẩu năm 2013 và sản lượng chè xuất khẩu năm 2018 là:

$\frac{125, 0}{262, 7} . 100 % \approx 48 %$

Lý thuyết Toán 7 Chương 1: Số hữu tỉ

1. Số hữu tỉ

- Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b} (a, b \in ℤ, b \neq 0)$ .

- Tập hợp các số hữu tỉ kí hiệu là ℚ.

Chú ý:

- Mỗi số nguyên là một số hữu tỉ.

- Các phân số bằng nhau là cách viết khác nhau của cùng một số hữu tỉ.

2. Biểu diễn số hữu tỉ trên trục số

- Tương tự số nguyên ta có thể biểu diễn mọi số hữu tỉ trên trục số.

- Điểm biểu diễn số hữu tỉ a được gọi là điểm a.

- Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số ta chọn một trong những phân số đó để biểu diễn. Thông thường ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.

- Nếu số hữu tỉ chưa viết dưới dạng phân số thì ta viết lại chúng dưới dạng phân số rồi biểu diễn phân số đó trên trục số.

3. Số đối của một số hữu tỉ

- Trên trục số hai số hữu tỉ phân biệt có điểm biểu diễn nằm về hai phía của điểm gốc O và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số hữu tỉ a, kí hiệu là –a.

- Số đối của số 0 là 0.

4. So sánh các số hữu tỉ

4.1 So sánh hai số hữu tỉ

Trong hai số hữu tỉ khác nhau bao giờ cũng có một số nhỏ hơn số kia.

- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a.

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.

- Số hữu tỉ 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương

- Nếu a < b và b < c thì a < c.

4.2 Cách so sánh hai số hữu tỉ

+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta dùng quy tắc đã học ở lớp 6 để so sánh.

+ Các trường hợp khác hai trường hợp trên, để so sánh hai số hữu tỉ ta viết chúng cùng về dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.

4.3 Minh họa trên trục số

Hai điểm x, y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số :

- Trên trục số nằm ngang: Nếu x < y hay y > x thì điểm x nằm bên trái điểm y.

- Trên trục số thẳng đứng: Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y.

5. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế

5.1 Quy tắc cộng, trừ hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

- Nếu hai số hữu tỉ cùng được viết dưới dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.

5.2 Tính chất của phép cộng các số hữu tỉ

- Phép cộng các số hữu tỉ có các tính chất giống với phép cộng các số nguyên: giao hoán, kết hợp, cộng với số 0, cộng với số đối.

- Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức chỉ có phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.

5.3 Quy tắc chuyển vế

Khi chuyển một số hạng tử vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:

x + y = z ⇒ x = z – y

x – y = z ⇒ x = z + y

6. Nhân, chia hai số hữu tỉ

6.1 Quy tắc nhân, chia hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

- Nếu hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.

6.2 Tính chất của phép nhân các số hữu tỉ

Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.

Nhận xét:

- Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là $\frac{1}{a}$ . Ta có $a \cdot \frac{1}{a} = 1$

- Số nghịch đảo của số hữu tỉ $\frac{1}{a}$ là a.

- Nếu a, b là hai số hữu tỉ và b ≠ 0 thì $a : b = a \cdot \frac{1}{b}$ .

7. Phép tính lũy thừa với số mũ tự nhiên

- Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x: $x^{n} = \underset{n thua so x}{\underset{⏟}{x . x . ... .x}}$ với $n \in ℕ^{*}$

Số x được gọi là cơ số, n gọi là số mũ.

- Quy ước x¹ = x.

Chú ý:

xⁿ đọc là “x mũ n” hoặc “x lũy thừa n” hoặc “lũy thừa bậc n của x”.

x² còn được gọi là “x bình phương” hay “bình phương của x”.

x³ còn gọi là “x lập phương” hay “lập phương của x”.

Chú ý: Để viết lũy thừa bậc n của phân số $\frac{a}{b}$ , ta phải viết $\frac{a}{b}$ trong dấu ngoặc ( ), tức là ${(\frac{a}{b})}^{n}$ .

8. Tích và thương của hai lũy thừa cùng cơ số

- Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:

x^m . xⁿ = x^{m+n $(m, n \in ℕ)$}.

- Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia :

x^m : xⁿ = x^{m – n} $(x \neq 0; m \geq n; m,n \in ℕ)$

- Quy ước x⁰ = 1 (x ≠ 0).

9. Lũy thừa của một lũy thừa

Khi tính lũy thừa của một lũy thừa ta giữ nguyên cơ số và nhân hai số mũ:

${(x^{m})}^{n} = x^{m . n} (m,n \in ℕ)$ .

10. Thứ tự thực hiện các phép tính

- Đối với biểu thức không có dấu ngoặc:

+ Khi biểu thức chỉ có các phép tính cộng và trừ (hoặc chỉ có phép tính nhân và chia), ta thực hiện phép tính theo thứ tự từ bên trái sang phải.

+ Khi biểu thức có các phép tính cộng, trừ, nhân, chia, ta thực hiện phép tính nhân và chia trước, rồi đến cộng và trừ.

+ Khi biểu thức có chứa các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép tính nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.

- Đối với biểu thức có chứa dấu ngoặc:

+ Khi biểu thức có chứa dấu ngoặc, ta thực hiện các phép tính trong ngoặc trước.

+ Khi các biểu thức có chứa các dấu ngoặc ( ), [ ]; { } thì thứ tự thực hiện phép tính như sau: ( ) → [ ] →{ }.

11. Quy tắc dấu ngoặc

- Khi bỏ dấu ngoặc có dấu “+” đằng trước, ta giữa nguyên dấu của các số hạng bên trong dấu ngoặc.

a + (b + c) = a + b + c

a + (b – c) = a + b – c

- Khi bỏ dấu ngoặc có dấu “–” đằng trước, ta phải đổi dấu của các số hạng bên trong dấu ngoặc: dấu “+” đổi thành dấu “–” và dấu “–” đổi thành dấu “+”.

a – (b + c) = a – b – c

a – (b – c) = a – b + c

Nhận xét: Nếu đưa các số hạng vào trong dấu ngoặc có dấu “–” đằng trước thì phải đổi dấu các số hạng đó.

12. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn

- Các số thập phân chỉ gồm hữu hạn chữ số sau dấu “,” được gọi là số thập phân hữu hạn.

- Các số thập phân mà trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi mãi được gọi là số thập phân vô hạn tuần hoàn. Chữ số hoặc cụm chữ số lặp đi lặp lại mãi mãi đó được gọi là chu kì của số thập phân vô hạn tuần hoàn.

13. Biểu diễn thập phân của số hữu tỉ

- Mỗi số hữu tỉ đều viết được dưới dạng phân số $\frac{a}{b} (a,b \in ℤ; b > 0)$ . Thực hiện phép tính

a : b ta có thể biểu diễn số hữu tỉ đó dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

- Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Bài 5: Biểu diễn thập phân của một số hữu tỉ

Bài 1: Số vô tỉ. Căn bậc hai số học

Bài 2: Tập hợp R các số thực

Bài 3: Giá trị tuyệt đối của một số thực