Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 2: Tập hợp R các số thực chi tiết sách Toán 7 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 2: Tập hợp R các số thực

Video bài giảng Tập hợp R các số thực - Cánh diều

I. Số thực

Giải Toán 7 trang 38 Tập 1

Hoạt động 1 trang 38 Toán lớp 7: a) Nêu hai ví dụ về số hữu tỉ

b) Nêu 2 ví dụ về số vô tỉ

Phương pháp giải:

Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}(a,b\in Z,b\ne 0)$

Những số không phải số hữu tỉ là số vô tỉ

Lời giải:

a) $\frac{3}{8};-0,2$ là các số hữu tỉ

b) $-\sqrt{3};\pi$ là các số vô tỉ

Hoạt động 2 trang 38 Toán lớp 7: a) Nêu biểu diễn thập phân của số hữu tỉ.

b) Nêu biểu diễn thập phân của số vô tỉ.

Phương pháp giải:

Nhớ lại dạng thập phân của số hữu tỉ, số vô tỉ đã học

Lời giải:

a) Số hữu tỉ được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn

b) Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn

II. Biểu diễn số thực trên trục số

Giải Toán 7 trang 39 Tập 1

Hoạt động 3 trang 39 Toán lớp 7: Biểu diễn các số hữu tỉ sau trên trục số: $-\frac{1}{2};1;1,25;\frac{7}{4}$

Phương pháp giải:

Vẽ trục số

Lời giải:

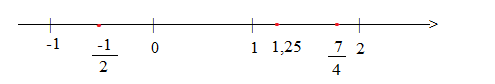
III. Số đối của một số thực

Giải Toán 7 trang 40 Tập 1

Luyện tập vận dụng 1 trang 40 Toán lớp 7: Tìm số đối của mỗi số sau:

$\frac{2}{-9};-0,5;-\sqrt{3}$

Phương pháp giải:

Số đối của số thực a là -a

Lời giải:

Số đối của $\frac{2}{-9};-0,5;-\sqrt{3}$ lần lượt là: $\frac{2}{9};0,5;\sqrt{3}$

Chú ý:

Số đối của  -a là  - (-a) = a

IV. So sánh các số thực

Hoạt động 5 trang 40 Toán lớp 7: a) So sánh hai số thập phân sau: -0,617 và -0,614.

b) Nêu quy tắc so sánh 2 số thập phân hữu hạn.

Phương pháp giải:

* So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương

* So sánh 2 số thập phân dương:

Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn

*So sánh 2 số thập phân âm:

Nếu a < b thì –a > - b

Lời giải:

a) Vì 0,617 > 0,614 nên -0,617 < -0,614

b) * So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương

* So sánh 2 số thập phân dương:

Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn

*So sánh 2 số thập phân âm:

Nếu a < b thì –a > - b

Giải Toán 7 trang 41 Tập 1

Luyện tập vận dụng 2 trang 41 Toán lớp 7: So sánh 2 số thực sau:

a) $1,(375)$ và $1\frac{3}{8}$

b) – 1,(27) và -1,272

Phương pháp giải:

Viết các số thực dưới dạng số thập phân. Đối với các số thập phân vô hạn tuần hoàn, ta đổi dạng viết có chu kì về dạng không viết chu kì

Lời giải:

a) Ta có: 1,(375) = 1,375375375…

$1\frac{3}{8}$ = 1,375

Vì 1,375375375 > 1,375 nên 1,(375) > $1\frac{3}{8}$

b) Ta có: -1,(27) = -1,272727…

Vì 1,272727… > 1,272 nên - 1,272727 < -1,272 hay – 1,(27) <  -1,272

Giải Toán 7 trang 42 Tập 1

Bài 1 trang 42 Toán lớp 7: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Nếu a $\in$ Z thì a $\in$ R

b) Nếu a $\in$ Q thì a $\in$ R

c) Nếu a $\in$ R thì a $\in$ Z

d) Nếu a $\in$ R thì a $\notin$ Q

Phương pháp giải:

Z: tập hợp các số nguyên: Z ={-3;-2;-1;0;1;2;3;…}

Q: tập hợp các số hữu tỉ

R: tập hợp các số thực

Lời giải:

a) Nếu a ∈ ℤ thì a ∈ ℝ.

Nếu a ∈ ℤ tức a là số nguyên, mà mọi số nguyên đều là số thực, do đó a ∈ ℝ.

Vậy phát biểu a) đúng.

b) Nếu a ∈ ℚ thì a ∈ ℝ.

Nếu a ∈ ℚ tức a là số hữu tỉ, mà mọi số hữu tỉ đều là số thực a ∈ ℝ.

Vậy phát biểu b) đúng.

c) Nếu a ∈ ℝ thì a ∈ ℤ.

Nếu a ∈ ℝ tức a là số thực, mà không phải số thực nào cũng là số nguyên.

Chẳng hạn, 1,4 ∈ ℝ nhưng 1,4 ∉ ℤ.

Do đó phát biểu c) sai.

d) Nếu a ∈ ℝ  thì a ∉ ℚ.

Nếu a ∈ ℝ tức a là số thực, mà không phải số thực nào cũng không phải là số hữu tỉ.

Chẳng hạn, $\frac{3}{4}\in ℝ$  nhưng $\frac{3}{4}\in \mathbb{Q}.$

Do đó phát biểu d) sai.

Vậy, trong các phát biểu trên: Phát biểu đúng là a và b; Phát biểu sai là c và d.

Bài 2 trang 42 Toán lớp 7: Tìm số đối của mỗi số sau:

$\frac{-8}{35};\frac{5}{-6};-\frac{18}{7};1,15;-21,54;-\sqrt{7};\sqrt{5}$

Phương pháp giải:

Số đối của số thực a là -a

Lời giải:

Số đối của $\frac{-8}{35};\frac{5}{-6};-\frac{18}{7};1,15;-21,54;-\sqrt{7};\sqrt{5}$ lần lượt là: $\frac{8}{35};\frac{5}{6};\frac{18}{7};-1,15;21,54;\sqrt{7};-\sqrt{5}$

Bài 3 trang 42 Toán lớp 7: So sánh:

a) -1,(81) và -1,812;

b) $2\frac{1}{7}$ và 2,142;

c) - 48,075…. và – 48,275….;

d) $\sqrt{5}$ và $\sqrt{8}$

Phương pháp giải:

a,b,c) Viết các số thực dưới dạng số thập phân.

* So sánh 2 số thập phân dương:

Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn

*So sánh 2 số thập phân âm:

Nếu a < b thì –a > - b

d) Nếu a > b > 0 thì $\sqrt{a}>\sqrt{b}$

Lời giải:

a) Ta có: 1,(81) = 1,8181…

Vì 1,8181… < 1,812 nên -1,8181… > -1,812 hay -1,(81) > -1,812

b) Ta có: $2\frac{1}{7}$ = 2,142857….

Vì 2,142857….> 2,142 nên $2\frac{1}{7}$ > 2,142

c) Vì 48,075… < 48,275… nên - 48,075…. > – 48,275…

d) Vì 5 < 8 nên $\sqrt{5}$ < $\sqrt{8}$

Bài 4 trang 42 Toán lớp 7: Tìm chữ số thích hợp cho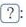 

Phương pháp giải:

* So sánh 2 số thập phân dương:

Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn

*So sánh 2 số thập phân âm:

Nếu a < b thì –a > - b

Lời giải:

Bài 5 trang 42 Toán lớp 7:a) Sắp xếp các số sau theo thứ tự tăng dần:

-2,63…; 3,(3); -2,75…; 4,62.

b) Sắp xếp các số sau theo thứ tự giảm dần:

1,371…; 2,065; 2,056…; -0,078…; 1,(37).

Phương pháp giải:

* So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương

* So sánh 2 số thập phân dương:

Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn

*So sánh 2 số thập phân âm:

Nếu a < b thì –a > - b

Lời giải:

a) Ta có: -2,63…; -2,75 < 0;

3,(3); 4,62 > 0

Vì 2,63…<  2,75 nên -2,63…> -2,75

Mà 3,(3) < 4,62

Nên -2,75 < -2,63…< 3,(3) < 4,62

Vậy các số trên theo thứ tự tăng dần là: -2,75 ; -2,63…; 3,(3) ; 4,62

b) Ta có: -0,078 < 0;

1,371…; 2,065; 2,056…; 1,(37) > 0

Ta có: 1,(37) = 1,3737….

Ta được: 2,065 > 2,056…> 1,3737…. > 1,371…

Nên 2,065 > 2,056…> 1,3737…. > 1,371… > -0,078

Vậy các số trên theo thứ tự giảm dần là: 2,065 ; 2,056…; 1,3737…. ; 1,371… ; -0,078

Lý thuyết Tập hợp R các số thực

1. Tập hợp số thực

1.1 Số thực

- Số hữu tỉ và số vô tỉ được gọi chung là số thực.

- Tập hợp các số thực được kí hiệu là ℝ.

Ví dụ: Các số 1,2 ; $\frac{-5}{3}$ ; $\sqrt{5}$ ; … là các số thực.

1.2 Biểu diễn thập phân của số thực

 - Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn. Ta có sơ đồ sau:

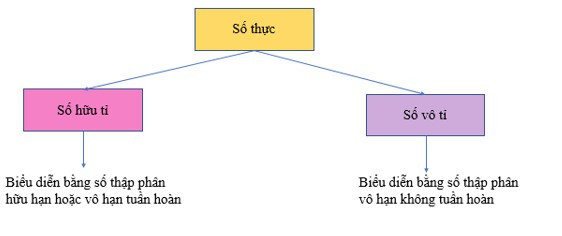
2. Biểu diễn số thực trên trục số

Tương tự như đối với số hữu tỉ, ta có thể biểu diễn mọi số thực trên trục số, khi đó điểm biểu diễn số thực x được gọi là điểm x.

Ví dụ: Biểu diễn các số thực sau trên trục số:

a) $\frac{-1}{2}$ và 2;

b) $\sqrt{2}$.

Hướng dẫn giải

a) Số $\frac{-1}{2}$ và 2 là hai số hữu tỉ, vì thế để biểu diễn hai số này trên trục số ta thực hiện như cách biểu diễn một số hữu tỉ trên trục số.

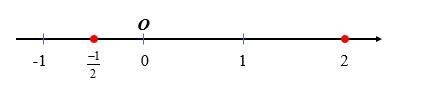
b) Số $\sqrt{2}$ là một số vô tỉ vì vậy để biểu diễn số $\sqrt{2}$ trên trục số ta làm như sau:

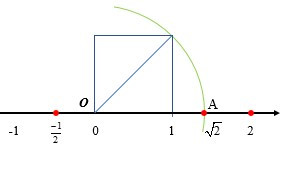
+ Vẽ một hình vuông với một cạnh là đoạn thẳng có hai đầu mút là điểm gốc 0 và điểm 1. Khi đó, đường chéo của hình vuông có độ dài cạnh bằng $\sqrt{2}$.

+ Vẽ một phần đường tròn tâm là điểm gốc 0, bán kính là $\sqrt{2}$, cắt trục số tại điểm A nằm bên phải gốc 0. Ta có OA = $\sqrt{2}$ và A là điểm biểu diễn $\sqrt{2}$.

Nhận xét:

- Không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

- Mỗi số thực được biểu diễn bởi một điểm trên trục số; Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Vậy trục số còn được gọi là trục số thực.

3. Số đối của một số thực

- Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số thực a kí hiệu là – a.

- Số đối của số 0 là 0.

Nhận xét: Số đối của – a là số a, tức là –(–a) = a.

Ví dụ:

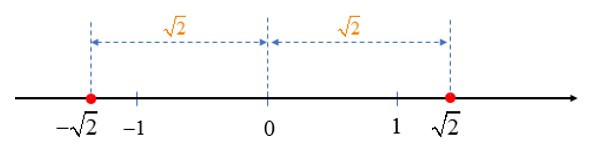
Số đối của số thực $\sqrt{2}$ là số thực $-\sqrt{2}$.

4. So sánh các số thực

4.1 So sánh hai số thực

Cũng như số hữu tỉ, trong hai số thực khác nhau luôn có một số nhỏ hơn số kia.

- Nếu số thực a nhỏ hơn số thực b thì ta biết a < b hay b > a.

- Số thực lớn hơn 0 gọi là số thực dương.

- Số thực nhỏ hơn 0 gọi là số thực âm.

- Số 0 không phải là số thực dương cũng không phải số thực âm.

- Nếu a < b và b < c thì a < c.

4.2 Cách so sánh hai số thực

- Ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.

- Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc: Với a, b là hai số thực dương, nếu a > b thì $\sqrt{\mathrm{a}}>\sqrt{\mathrm{b}}$.

Ví dụ: So sánh các số thực sau:

a) –1,(27) và –1,272;

b) $\sqrt{7}$ và $\sqrt{8}$.

Hướng dẫn giải

a) Ta viết –1,(27) = –1,27272727….. sau đó ta so sánh với –1,272.

Hai số –1,27272727… và –1,2720 có phần nguyên và đến hàng phần nghìn giống nhau, cặp chữ số khác nhau đầu tiên bắt đầu từ hàng phần chục nghìn.

Do 7 > 0 nên 1,27272727…..> 1,2720, suy ra  –1,27272727…..< –1,2720.

Vậy –1,(27) < –1,272.

b) Ta có: 0 < 7 < 8 nên $\sqrt{7}$ < $\sqrt{8}$.

4.3 Minh họa trên trục số

Giả sử hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số nằm ngang. Ta có nhận xét sau :

- Nếu x < y hay y > x thì điểm x nằm bên trái điểm y;

- Ngược lại nếu điểm x nằm bên trái điểm y thì x < y hay y > x.

Đối với hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số thẳng đứng, ta cũng có nhận xét sau :

- Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y;

- Ngược lại, nếu điểm x nằm phía dưới điểm y thì x < y hay y > x.

Ví dụ:

+ Vì $\frac{-3}{2}$ < –1 nên trên trục số nằm ngang, điểm $\frac{-3}{2}$ nằm bên trái điểm –1.

+ Điểm $\sqrt{2}$ nằm bên trái điểm $\sqrt{5}$, vì vậy $\sqrt{2}$ < $\sqrt{5}$.

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Bài 1: Số vô tỉ. Căn bậc hai số học

Bài 3: Giá trị tuyệt đối của một số thực

Bài 4: Làm tròn và ước lượng

Bài 5: Tỉ lệ thức