Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp)

hoa Ngày: 23-09-2022 Lớp 8

2.8 K

Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp), chi tiết nhất giúp học sinh dễ dàng làm bài tập Những hằng đẳng thức đáng nhớ (tiếp) lớp 8.

Giải bài tập Toán lớp 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp)

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 14 sgk Toán 8 Tập 1: Tính $(a + b) (a^{2} - a b + b^{})$ (với $a, b$ là hai số tùy ý).

Phương pháp giải: Áp dụng quy tắc nhân đa thức với đa thức

Lời giải:

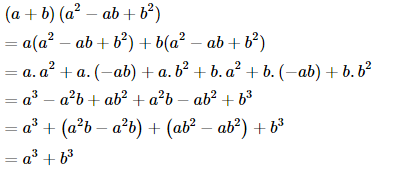
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 4)

Trả lời câu hỏi 2 trang 15 sgk Toán 8 Tập 1: Phát biểu hằng đẳng thức (6) bằng lời.

Áp dụng:

a) Viết $x^{3} + 8$ dưới dạng tích

b) Viết $(x + 1) (x^{2} - x + 1)$ dưới dạng tổng

Phương pháp giải: Hằng đẳng thức $A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2})$ (6)

Lời giải:

Phát biểu: Tổng của lập phương hai biểu thức bằng tích của tổng hai biểu thức và bình phương thiếu của hiệu hai biểu thức đó.

Áp dụng:

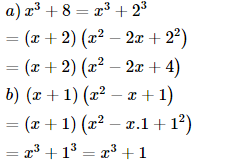
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 5)

Trả lời câu hỏi 3 trang 15 sgk Toán 8 Tập 1: Tính $(a - b) (a^{2} + a b + b^{2})$ (với $a, b$ là các số tùy ý).

Lời giải:

$\begin{aligned} (a - b) (a^{2} + a b + b^{2}) \\ = a (a^{2} + a b + b^{2}) - b (a^{2} + a b + b^{2}) \\ = a . a^{2} + a . a b + a . b^{2} + (- b) . a^{2} + (- b) . a b + (- b) . b^{2} \\ = a^{3} + a^{2} b + a b^{2} - a^{2} b - a b^{2} - b^{3} \\ = a^{3} + (a^{2} b - a^{2} b) + (a b^{2} - a b^{2}) - b^{3} \\ = a^{3} - b^{3} \end{aligned}$

Trả lời câu hỏi 4 trang 15 sgk Toán 8 Tập 1: Phát biểu hằng đẳng thức (7) bằng lời.

Áp dụng:

a) Tính $(x - 1) (x^{2} + x + 1)$

b) Viết $8 x^{3} - y^{3}$ dưới dạng tích

c) Hãy đánh dấu x vào ô có đáp án đúng của tích: $(x + 2) (x^{2} - 2 x + 4)$

Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 1)

Phương pháp giải: Hằng đẳng thức $A^{3} - B^{3} = (A - B) (A^{2} + A B + B^{2})$ (7)

Lời giải:

Phát biểu: Hiệu của lập phương hai biểu thức bằng tích của hiệu hai biểu thức và bình phương thiếu của tổng hai biểu thức đó.

Áp dụng:

$\begin{array}{l} a) (x - 1) (x^{2} + x + 1) \\ = (x - 1) (x^{2} + x .1 + 1^{2}) \\ = x^{3} - 1^{3} = x - 1 \\ b) 8 x^{3} - y^{3} \\ = {(2 x)}^{3} - y^{3} \\ = (2 x - y) [{(2 x)}^{2} + 2 x . y + y^{2}] \\ = (2 x - y) (4 x^{2} + 2 x y + y^{2}) \\ c) (x + 2) (x^{2} - 2 x + 4) \\ = (x + 2) (x^{2} - x .2 + 2^{2}) \\ = x^{3} + 2^{3} = x^{3} + 8 \end{array}$

Vậy ta đánh dấu x vào ô như sau:
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 3)

Câu hỏi và bài tập (trang 16, 17 sgk Toán 8 Tập 1)

Bài 30 trang 16 sgk Toán 8 tập 1: Rút gọn các biểu thức sau:

a) $(x + 3) (x^{2} - 3 x + 9) - (54 + x^{3})$

b) $(2 x + y) (4 x^{2} - 2 x y + y^{2}) - (2 x - y) (4 x^{2} + 2 x y + y^{2})$

Phương pháp giải: Áp dụng: Hằng đẳng thức tổng hai lập phương, quy tắc phá dấu ngoặc.

$A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2})$

Lời giải:

$\begin{aligned} (x + 3) (x^{2} - 3 x + 9) - (54 + x^{3}) \\ = (x + 3) (x^{2} - x .3 + 3^{2}) - (54 + x^{3}) \\ = x^{3} + 3^{3} - (54 + x^{3}) \\ = x^{3} + 27 - 54 - x^{3} \\ = (x^{3} - x^{3}) + (27 - 54) \\ = - 27 \end{aligned}$

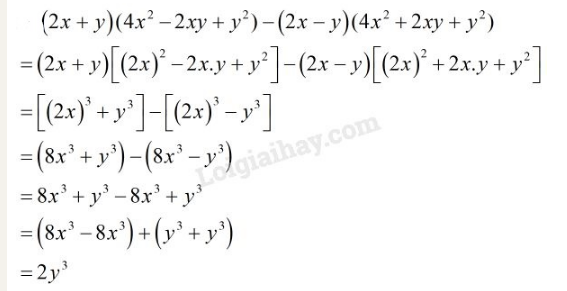
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 6)

Bài 31 trang 16 sgk Toán 8 tập 1: Chứng minh rằng:

a) $a^{3} + b^{3} = {(a + b)}^{3} - 3 a b (a + b)$

b) $a^{3} - b^{3} = {(a - b)}^{3} + 3 a b (a - b)$

Áp dụng: Tính $a^{3} + b^{3}$ , biết $a . b = 6$ và $a + b = - 5.$

Phương pháp giải: - Biến đổi vế phải của đẳng thức về vế trái đẳng thức.

- Áp dụng các hằng đẳng thức đáng nhớ: lập phương của một tổng hoặc một hiệu, tổng (hiệu) hai lập phương, nhân đơn thức với đa thức.

Lời giải:

a) $a^{3} + b^{3} = {(a + b)}^{3} - 3 a b (a + b)$

Biến đổi vế phải:

$\begin{aligned} {(a + b)}^{3} - 3 a b (a + b) \\ = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} + (- 3 a b) . a + (- 3 a b) . b \\ = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} - 3 a^{2} b - 3 a b^{2} \\ = a^{3} + (3 a^{2} b - 3 a^{2} b) + (3 a b^{2} - 3 a b^{2}) + b^{3} \\ = a^{3} + b^{3} \end{aligned}$

Vậy $a^{3} + b^{3} = {(a + b)}^{3} - 3 a b (a + b)$

b) $a^{3} - b^{3} = {(a - b)}^{3} + 3 a b (a - b)$

Biến đổi vế phải:

$\begin{aligned} {(a - b)}^{3} + 3 a b (a - b) \\ = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} + 3 a b . a + 3 a b . (- b) \\ = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} + 3 a^{2} b - 3 a b^{2} \\ = a^{3} + (3 a^{2} b - 3 a^{2} b) + (3 a b^{2} - 3 a b^{2}) - b^{3} \\ = a^{3} - b^{3} \end{aligned}$

Vậy $a^{3} - b^{3} = {(a - b)}^{3} + 3 a b (a - b)$

Áp dụng:

Với $a b = 6, a + b = - 5$ , ta được:

$\begin{aligned} a^{3} + b^{3} = {(a + b)}^{3} - 3 a b (a + b) \\ = {(- 5)}^{3} - 3.6. (- 5) \\ = - 125 + 90 = - 35 \end{aligned}$

Bài 32 trang 16 sgk Toán 8 tập 1: Điền các đơn thức thích hợp vào ô trống:

Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 7)

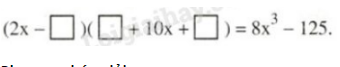
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 8)

Phương pháp giải: Áp dụng: Hằng đẳng thức tổng hai lập phương.

$A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2})$

Lời giải:

a) Ta có:

$\begin{aligned} 27 x^{3} + y^{3} \\ = {(3 x)}^{3} + y^{3} \\ = (3 x + y) [{(3 x)}^{2} - 3 x . y + y^{2}] \\ = (3 x + y) (9 x^{2} - 3 x y + y^{2}) \end{aligned}$

Suy ra:

$(3 x + y) ($ $9 x^{2} - 3 x y + y^{2}$ $) = 27 x^{3} + y^{3}$

b) Ta có:

$\begin{aligned} 8 x^{3} - 125 \\ = {(2 x)}^{3} - 5^{3} \\ = (2 x - 5) [{(2 x)}^{2} + 2 x .5 + 5^{2}] \\ = (2 x - 5) (4 x^{2} + 10 x + 25) \end{aligned}$

Suy ra:

$(2 x -$ $5$ $) ($ $4 x^{2}$ $+ 10 x +$ $25$ $) = 8 x^{3} - 125$

Bài 33 trang 16 sgk Toán 8 tập 1: Tính:

a) $\begin{aligned} {(2 + x y)}^{2} \end{aligned}$ ;

b) $\begin{aligned} {(5 - 3 x)}^{2} \end{aligned}$ ;

c) $\begin{aligned} (5 - x^{2}) (5 + x^{2}) \end{aligned}$ ;

d) $\begin{aligned} {(5 x - 1)}^{3} \end{aligned}$ ;

e) $\begin{aligned} (2 x - y) (4 x^{2} + 2 x y + y^{2}) \end{aligned}$ ;

f) $\begin{aligned} (x + 3) (x^{2} - 3 x + 9) \end{aligned}$ .

Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

$\begin{aligned} {(2 + x y)}^{2} = 2^{2} + 2.2. x y + {(x y)}^{2} \\ = 4 + 4 x y + x^{2} y^{2} \end{aligned}$

$\begin{aligned} {(5 - 3 x)}^{2} = 5^{2} - 2.5.3 x + {(3 x)}^{2} \\ = 25 - 30 x + 9 x^{2} \end{aligned}$

$\begin{aligned} (5 - x^{2}) (5 + x^{2}) = 5^{2} - (x^{2})^{2} \\ = 25 - x^{4} \end{aligned}$

$\begin{aligned} {(5 x - 1)}^{3} = {(5 x)}^{3} - 3. {(5 x)}^{2} .1 + 3.5 x {.1}^{2} - 1^{3} \\ = 125 x^{3} - 75 x^{2} + 15 x - 1 \end{aligned}$

$\begin{aligned} (2 x - y) (4 x^{2} + 2 x y + y^{2}) \\ = (2 x - y) [{(2 x)}^{2} + 2 x . y + y^{2}] \\ = {(2 x)}^{3} - y^{3} = 8 x^{3} - y^{3} \end{aligned}$

$\begin{aligned} (x + 3) (x^{2} - 3 x + 9) \\ = (x + 3) (x^{2} - x .3 + 3^{2}) \\ = x^{3} + 3^{3} = x^{3} + 27 \end{aligned}$

Bài 34 trang 17 sgk Toán 8 tập 1: Rút gọn các biểu thức sau:

a) ${(a + b)}^{2} - {(a - b)}^{2}$ ;

b) ${(a + b)}^{3} - {(a - b)}^{3} - 2 b^{3}$ ;

c) ${(x + y + z)}^{2} - 2 (x + y + z) (x + y) + {(x + y)}^{2}$ .

Lời giải:

Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.

$1) {(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

$2) {(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

$3) A^{2} - B^{2} = (A + B) (A - B)$

Lời giải:

$\begin{aligned} {(a + b)}^{2} - {(a - b)}^{2} \\ = (a^{2} + 2 a b + b^{2}) - (a^{2} - 2 a b + b^{2}) \\ = a^{2} + 2 a b + b^{2} - a^{2} + 2 a b - b^{2} \\ = (a^{2} - a^{2}) + 2 a b + 2 a b + (b^{2} - b^{2}) \\ = 4 a b \end{aligned}$

Cách 2:

$\begin{aligned} {(a + b)}^{2} - {(a - b)}^{2} \\ = [(a + b) + (a - b)] . [(a + b) - (a - b)] \\ = (a + b + a - b) (a + b - a + b) \\ = 2 a .2 b = 4 a b \end{aligned}$

Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.

$4) {(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3}$

$5) {(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

$7) A^{3} - B^{3} = (A - B) (A^{2} + A B + B^{2})$

Lời giải:

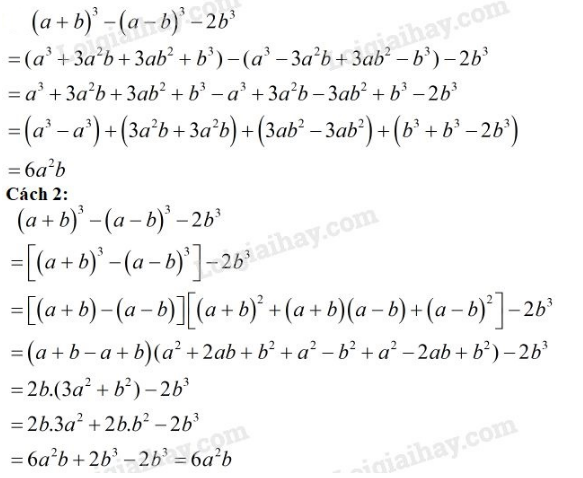
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 1)

Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.

$2) {(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Hoặc áp dụng kết quả:

${(x + y + z)}^{2} = x^{2} + y^{2} + z^{2} + 2 x y + 2 y z + 2 x z$

Lời giải:

Đặt $A = x + y + z; B = x + y$

Ta có:

$\begin{aligned} {(x + y + z)}^{2} - 2 (x + y + z) (x + y) + {(x + y)}^{2} \\ = A^{2} - 2 A B + B^{2} = {(A - B)}^{2} \\ = {[(x + y + z) - (x + y)]}^{2} \\ = {(x + y + z - x - y)}^{2} = z^{2} \end{aligned}$

Cách 2:

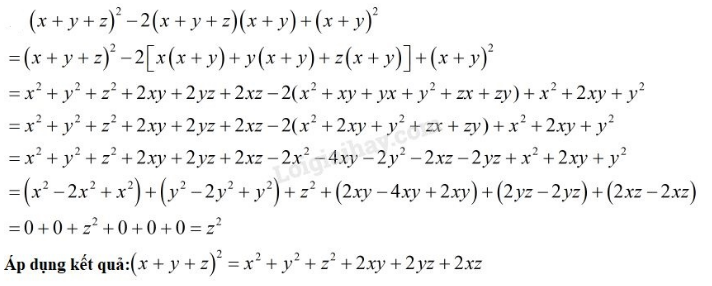
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 2)

Bài 35 trang 17 sgk Toán 8 tập 1: Tính nhanh:

a) $\begin{aligned} 34^{2} + 66^{2} + 68.66 \end{aligned}$

b) $\begin{aligned} 74^{2} + 24^{2} - 48.74 \end{aligned}$

Phương pháp giải: Áp dụng hằng đẳng thức: bình phương của một tổng.

$1) {(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

$\begin{aligned} 34^{2} + 66^{2} + 68.66 \\ = 34^{2} + 68.66 + 66^{2} \\ = 34^{2} + 2.34.66 + 66^{2} \\ = {(34 + 66)}^{2} \\ = 100^{2} = 10000 \end{aligned}$

$\begin{aligned} 74^{2} + 24^{2} - 48.74 \\ = 74^{2} - 48.74 + 24^{2} \\ = 74^{2} - 2.74.24 + 24^{2} \\ = {(74 - 24)}^{2} \\ = 50^{2} = 2500 \end{aligned}$

Bài 36 trang 17 sgk Toán 8 tập 1: Tính giá trị của biểu thức:

a) $x^{2} + 4 x + 4$ tại $x = 98$ ;

b) $x^{3} + 3 x^{2} + 3 x + 1$ tại $x = 99$

Phương pháp giải: Áp dụng hằng đẳng thức bình phương của một tổng để rút gọn biểu thức, sau đó thay giá trị của $x$ để tính giá trị của biểu thức.

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

$x^{2} + 4 x + 4$

$= x^{2} + 2. x .2 + 2^{2}$

$= {(x + 2)}^{2}$

Với $x = 98$ ta có: ${(98 + 2)}^{2} = 100^{2} = 10000$ .

$x^{3} + 3 x^{2} + 3 x + 1$

$= x^{3} + 3. x^{2} .1 + 3. x {.1}^{2} + 1^{3}$

$= {(x + 1)}^{3}$

Với $x = 99$ ta có: ${(99 + 1)}^{3} = 100^{3} = 1000000$ .

Bài 37 trang 17 sgk Toán 8 tập 1: Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu)
Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 3)

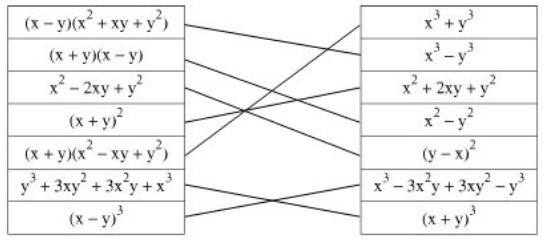
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ.

$1) {(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

$2) {(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

$3) A^{2} - B^{2} = (A + B) (A - B)$

$4) {(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3}$

$5) {(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

$6) A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2})$

$7) A^{3} - B^{3} = (A - B) (A^{2} + A B + B^{2})$

Lời giải:

Giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp) (ảnh 4)

Bài 38 trang 17 sgk Toán 8 tập 1: Chứng minh các đẳng thức sau:

a) ${(a - b)}^{3} = - {(b - a)}^{3}$ ;

b) ${(- a - b)}^{2} = {(a + b)}^{2}$

Phương pháp giải: Áp dụng hằng đẳng thức đáng nhớ: lập phương của một hiệu, sử dụng quy tắc dấu ngoặc, ta biến đổi một vế của đẳng thức thành vế còn lại, ta được điều phải chứng minh.

$5) {(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

Lời giải:

a) ${(a - b)}^{3} = - {(b - a)}^{3}$

Biến đổi vế phải thành vế trái:

$\begin{aligned} - {(b - a)}^{3} = - (b^{3} - 3 b^{2} a + 3 b a^{2} - a^{3}) \\ = - b^{3} + 3 b^{2} a - 3 b a^{2} + a^{3} \\ = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} \\ = {(a - b)}^{3} \end{aligned}$

Vậy ${(a - b)}^{3} = - {(b - a)}^{3}$

Cách 2: Sử dụng quy tắc dấu ngoặc

$\begin{aligned} {(a - b)}^{3} = {[- (b - a)]}^{3} = {[(- 1) . (b - a)]}^{3} \\ = {(- 1)}^{3} . {(b - a)}^{3} = (- 1) . {(b - a)}^{3} \\ = - {(b - a)}^{3} \end{aligned}$

${(- a - b)}^{2} = {(a + b)}^{2}$

Biến đổi vế trái thành vế phải:

$\begin{aligned} {(- a - b)}^{2} = {[(- a) + (- b)]}^{2} \\ = {(- a)}^{2} + 2. (- a) . (- b) + {(- b)}^{2} \\ = a^{2} + 2 a b + b^{2} = {(a + b)}^{2} \end{aligned}$

Vậy ${(- a - b)}^{2} = {(a + b)}^{2}$

Cách 2: Sử dụng quy tắc dấu ngoặc

$\begin{aligned} {(- a - b)}^{2} = {[- (a + b)]}^{2} \\ = {[(- 1) . (a + b)]}^{2} \\ = {(- 1)}^{2} . {(a + b)}^{2} \\ = 1. {(a + b)}^{2} = {(a + b)}^{2} \end{aligned}$

Lý thuyết những hằng đẳng thức đáng nhớ (tiếp)

6. Tổng hai lập phương: Tổng của lập phương hai biểu thức bằng tích của tổng hai biểu thức và bình phương thiếu của hiệu hai biểu thức đó.

$A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2})$

7. Hiệu hai lập phương: Hiệu của lập phương hai biểu thức bằng tích của hiệu hai biểu thức và bình phương thiếu của tổng hai biểu thức đó.

$A^{3} - B^{3} = (A - B) (A^{2} + A B + B^{2})$

Ta có bảy hằng đẳng thức đáng nhớ

$1. {(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

$2. {(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

$3. A^{2} - B^{2} = (A + B) (A - B)$

$4. {(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3}$

$5. {(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

$6. A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2})$

$7. A^{3} - B^{3} = (A - B) (A^{2} + A B + B^{2})$

Các dạng toán cơ bản

Dạng 1: Rút gọn biểu thức

Phương pháp: Sử dụng các hằng đẳng thức và phép nhân đa thức để biến đổi.

Ví dụ: Rút gọn biểu thức $(x - 1) (x^{2} + x + 1)$

Ta có: $(x - 1) (x^{2} + x + 1)$ $= (x - 1) (x^{2} + x .1 + 1^{2}) = x^{3} - 1$

Dạng 2: Tìm $x$

Phương pháp: Sử dụng các hằng đẳng thức và phép nhân đa thức để biến đổi để đưa về dạng tìm $x$ thường gặp

Ví dụ: Tìm $x$ biết $(x + 2) (x^{2} - 2 x + 4) = 8$

Ta có:

$\begin{array}{l} (x + 2) (x^{2} - 2 x + 4) = 8 \\ \Rightarrow x^{3} + 2^{3} = 8 \\ \Rightarrow x^{3} + 8 = 8 \\ \Rightarrow x^{3} = 0 \\ \Rightarrow x = 0 \end{array}$