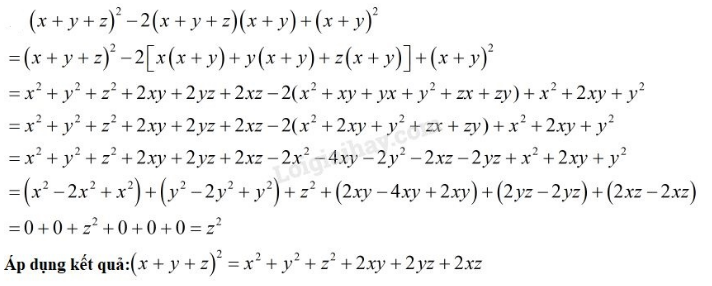Với giải bài 34 trang 17 Toán lớp 8 chi tiết trong Bài 5: Những hàng đẳng thức đáng nhớ (tiếp) giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 5: Những hàng đẳng thức đáng nhớ (tiếp)
Bài 34 trang 17 sgk Toán 8 tập 1: Rút gọn các biểu thức sau:
a) ;
b) ;
c) .
Lời giải:
a)
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.
Lời giải:
Cách 2:
b)
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.
Lời giải:
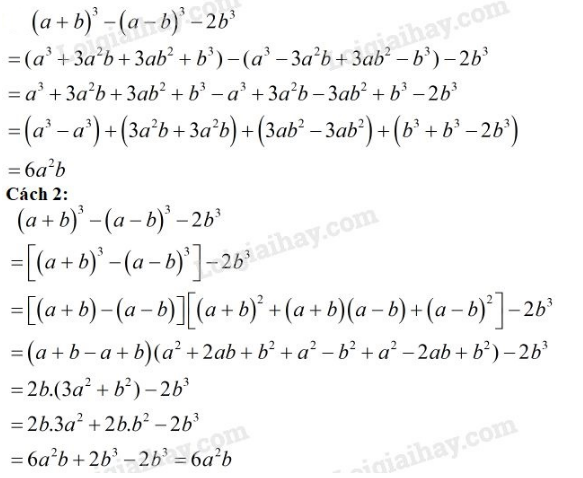
c)
Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.
Hoặc áp dụng kết quả:
Lời giải:
Đặt
Ta có:
Cách 2: