Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ chi tiết sách Toán 7 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ
Video bài giảng Cộng, trừ, nhân, chia số hữu tỉ - Cánh diều
I. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế.
Hoạt động 1 trang 12 Toán lớp 7: Thực hiện các phép tính sau:
a); b).
Phương pháp giải:
a) Quy đồng mẫu hai phân số rồi thực hiện phép cộng hai phân số.
b) Áp dụng quy tắc trừ hai số thập phân.
Lời giải:
a)
b)
a);
b).
Phương pháp giải:
- Đưa hai số về phép cộng, trừ hai phân số.
- Quy đồng mẫu hai phân số rồi thực hiện phép cộng hai phân số.
Lời giải chi tiết:
a);
b)
Hoạt động 2 trang 13 Toán lớp 7: Nêu tính chất của phép cộng các số nguyên
Phương pháp giải:
Nhớ lại tính chất của phép cộng các số nguyên đã học.
Lời giải:
Tính chất giao hoán:
Tính chất kết hợp:
Cộng với số 0: .
Cộng với số đối:
Luyện tập vận dụng 2 trang 13 Toán lớp 7: Tính một cách hợp lí:
a);
b).
Phương pháp giải:
Sử dụng tính chất giao hoán của các số hữu tỉ.
Lời giải:
a).
b)
Hoạt động 3 trang 13 Toán lớp 7: a) Tìm số nguyên x, biết:
b) Trong tập hợp các số nguyên, nếu quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.
Phương pháp giải:
a) Áp dụng quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.
b) Nhắc lại quy tắc đã được học
Lời giải:
a)
Vậy x=-8.
b) Quy tắc: Muốn tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại, ta lấy tổng trừ đi số hạng kia.
Luyện tập vận dụng 3 trang 14 Toán lớp 7: Tìm x, biết:
a);
b).
Phương pháp giải:
Sử dụng quy tắc chuyển vế.
Lời giải:
a)
Vậy .
b)
Vậy .
II. Nhân, chia hai số hữu tỉ.
Hoạt động 4 trang 14 Toán lớp 7: Thực hiện các phép tính sau:
a) b) c).
Phương pháp giải:
- Câu a và b: áp dụng quy tắc nhân, chia hai phân số.
- Câu c: Đưa về dạng phép nhân hai phân số, rồi thực hiện phép tính.
Lời giải:
a)
b)
c).
Luyện tập vận dụng 4 trang 14 Toán lớp 7: Giải bài toán nêu trong phần mở đầu.
Phương pháp giải:
Độ dài đèo Hải Vân = Độ dài hầm Hải Vân : .
Lời giải:
Độ dài đèo Hải Vân là:
Phương pháp giải:
Thời gian ô tô đi hết cả quãng đường AB = Thời gian đi : Quãng đường đi được.
Lời giải:
Thời gian ô tô đi hết quãng đường AB là: (h)
Hoạt động 5 trang 15 Toán lớp 7: Nêu tính chất của phép nhân các số nguyên.
Phương pháp giải:
Nhớ lại tính chất của phép nhân các số nguyên đã học.
Lời giải:
Tính chất giao hoán:
Tính chất kết hợp:
Nhân với số 1: .
Tính chất phân phối của phép nhân đối với phép cộng:
Luyện tập vận dụng 6 trang 15 Toán lớp 7: Tính một cách hợp lí:
a)
b)
Phương pháp giải:
Tính chất giao hoán:
Tính chất kết hợp:
Tính chất phân phối của phép nhân đối với phép trừ:
Lời giải:
a)
b)
Hoạt động 6 trang 15 Toán lớp 7: Nêu phân số nghịch đảo của phân số .
Phương pháp giải:
Phân số cần tìm là phân số nhân với phân số được tích bằng 1.
Lời giải:
Phân số nghịch đảo của phân số là:
Luyện tập vận dụng 7 trang 16 Toán lớp 7: Tìm số nghịch đảo của mỗi số hữu tỉ sau:
a); b)
Phương pháp giải:
a)Đưa hỗn số về phân số rồi tìm số nghịch đảo
Phân số nghịch đảo của phân số là:
b) Số nghịch đảo của số a là: .
Lời giải:
a)Ta có:
Số nghịch đảo của là: .
b) Số nghịch đảo của là:
Chú ý: Ta phải chuyển hỗn số về phân số trước khi tìm số nghịch đảo.
Bài tập.
Bài 1 trang 16 Toán lớp 7: Tính:
a); b); c).
Phương pháp giải:
Đưa các phép tính về phép cộng, trừ các phân số.
Áp dụng tính chất giao hoán và kết hợp để tính nhanh (nếu có thể).
Lời giải:
a);
b);
c)
Bài 2 trang 16 Toán lớp 7: Tính:
a); b); c).
Phương pháp giải:
Lời giải:
a)
b);
c)
Bài 3 trang 16 Toán lớp 7: Tính một cách hợp lí:
a); b);
Phương pháp giải:
a) Áp dụng tính chất giao hoán và kết hợp của phép cộng.
b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
Lời giải:
a)
b)
Bài 4 trang 16 Toán lớp 7: Tìm x, biết:
a);
b)
c);
d).
Phương pháp giải:
Lời giải:
a)
Vậy .
b)
Vậy .
c)
Vậy
d)
Vậy .
Phương pháp giải:
- Tính số tiền lãi = Số tiền gốc.
- Tính số tiền rút ra
- Tính số tiền còn lại.
Lời giải:
Số tiền lãi là: (triệu đồng)
Số tiền gốc và lãi của bác Nhi sau 1 năm là:
60 + 3,9 = 63,9 (triệu đồng)
Số tiền bác Nhi rút ra là: . 63,9 = 21,3 (triệu đồng)
Số tiền còn lại của bác Nhi trong ngân hàng là: 63,9 – 21,3 = 42,6 (triệu đồng).
Bài 6 trang 16 Toán lớp 7:Tính diện tích mặt bằng của ngôi nhà được mô tả như Hình 7 (các số đo trên hình tính theo đơn vị mét):
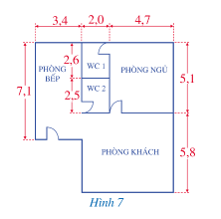
Phương pháp giải:
Lời giải:
Diện tích mặt bằng của ngôi nhà là:
(m2)
Phương pháp giải:
Tính khoảng cách thực tế từ ổ cắm điện đến vòi nước, theo bản đồ: Khoảng cách trên bản đồ:tỉ lệ
=>So sánh với khoảng cách và kết luận.
Lời giải:
Theo bản đồ, khoảng cách thực tế từ ổ cắm điện đến vòi nước là:
(cm)
Vì 50 cm < 60 cm nên khoảng cách trên bản vẽ như vậy không phù hợp với yêu cầu của kiến trúc sư.
Lý thuyết Cộng, trừ, nhân, chia số hữu tỉ
1. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế
1.1 Quy tắc cộng, trừ hai số hữu tỉ
- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.
- Nếu hai số hữu tỉ cùng được viết dưới dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.
Ví dụ: Tính
a) ;
b) 1,205 – 2,31.
Hướng dẫn giải
a) Ta có . Do đó:
.
b) 1,205 – 2,31= 1,205 + (–2,31) = – (2,31 – 1,205) = –1,105.
1.2 Tính chất của phép cộng các số hữu tỉ
- Phép cộng các số hữu tỉ có các tính chất giống với phép cộng các số nguyên: giao hoán, kết hợp, cộng với số 0, cộng với số đối.
- Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức chỉ có phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.
Ví dụ: Tính một cách hợp lý
Ta có:
1.3 Quy tắc chuyển vế
Khi chuyển một số hạng tử vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:
x + y = z ⇒ x = z – y
x – y = z ⇒ x = z + y
Ví dụ: Tìm x, biết
a) ;
b) .
Hướng dẫn giải
a)
Vậy .
Vậy x = – 7,8.
2. Nhân, chia hai số hữu tỉ
2.1 Quy tắc nhân, chia hai số hữu tỉ
- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
- Nếu hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.
Ví dụ:
a) ;
b) .
Hướng dẫn giải
a) Ta viết và
Khi đó:
b) Ta có thể viết
Khi đó .
2.2 Tính chất của phép nhân các số hữu tỉ
Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.
Ví dụ: Tính một cách hợp lý:
a) ;
b) .
Hướng dẫn giải
a)
b) Ta có . Khi đó:
.
Nhận xét:
- Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là . Ta có
- Số nghịch đảo của số hữu tỉ là a.
- Nếu a, b là hai số hữu tỉ và b ≠ 0 thì .
Ví dụ:
Số nghịch đảo của là
Số nghịch đảo của 0,3 là .
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Bài 1: Tập hợp Q các số hữu tỉ
Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ