Với giải sách bài tập Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Giải Toán 7 trang 13 tập 1

Bài 11 trang 13 Toán 7 tập 1: Tính:

a) −6,07 + 3,58;

b) $\frac{3}{5}+\left(-4\right)$;

c) $1\frac{3}{5}-\frac{-7}{11}$;

d) $\frac{-7}{13}+0,6$;

e) $-1,221.\frac{2}{-5}$;

g) $\frac{-17}{7}:0,25$.

Lời giải:

a) −6,07 + 3,58 = −(6,07 − 3,58) = −2,49;

b) $\frac{3}{5}+\left(-4\right)$= 0,6 + (−4)

= −(4 – 0,6) = −3,4;

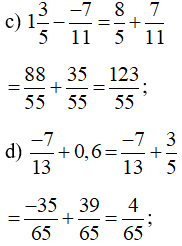
e) $-1,221.\frac{2}{-5}$ = 1,221 . 0,4 = 0,4884;

g) $\frac{-17}{7}:0,25=\frac{-17}{7}:\frac{1}{4}$

$=\frac{-17}{7}.4=\frac{-68}{7}$.

Bài 12 trang 13 Toán 7 tập 1: So sánh giá trị của các biểu thức sau:

$A=10\frac{5}{7}.(-0,7)$; $B=2\frac{4}{5}:(-0,4)$; $C=(-4,5).1\frac{31}{45}$.

Lời giải:

Ta có:

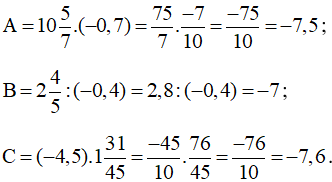
Vì −7,6 < −7,5 < −7 nên ta có: A < A < B.

Bài 13 trang 13 Toán 7 tập 1: Tính một cách hợp lí:

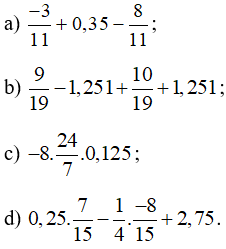
Lời giải:

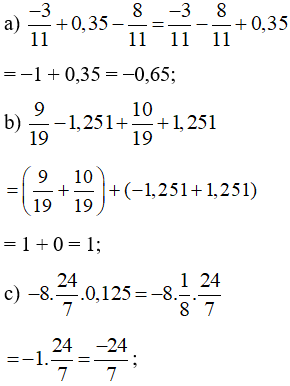
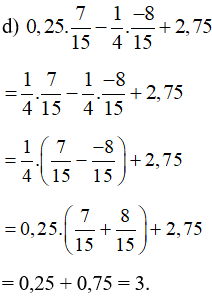
Bài 14 trang 13 Toán 7 tập 1: Tìm số hữu tỉ x, biết:

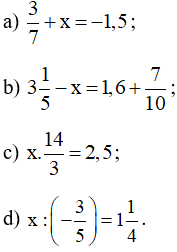
Lời giải:

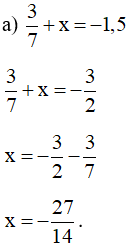
Vậy $x=-\frac{27}{14}$.

b) $3\frac{1}{5}-x=1,6+\frac{7}{10}$

3,2 – x = 1,6 + 0,7

3,2 – x = 2,3

x = 3,2 – 2,3

x = 0,9.

Vậy x = 0,9.

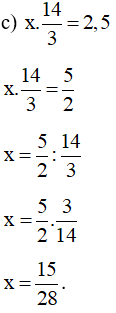
Vậy $x=\frac{15}{28}$.

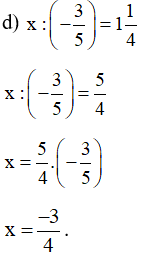
Vậy $x=\frac{-3}{4}$.

Giải Toán 7 trang 14 tập 1

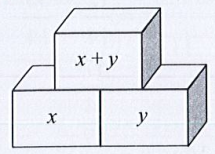
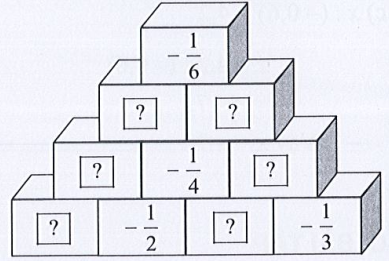
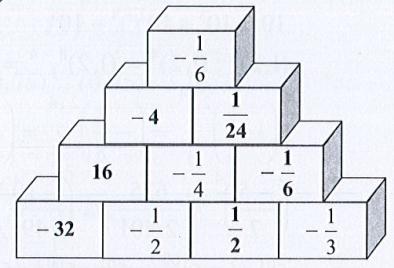
Bài 15 trang 14 Toán 7 tập 1: Tìm số thích hợp cho $\boxed{?}$ trong các hình tháp dưới đây theo quy tắc.

Quy tắc 1:

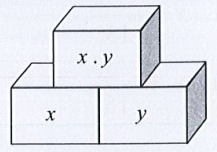
Quy tắc 2:

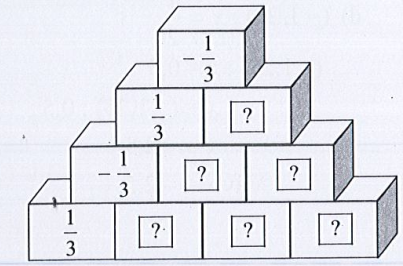
a) Áp dụng Quy tắc 1, ta có tháp:

b) Áp dụng Quy tắc 2, ta có tháp:

Lời giải:

a) Áp dụng Quy tắc 1 thì tổng của hai ô trống bên dưới bằng ô phía trên liền với 2 ô đó.

Chẳng hạn ta tính:

∙ $\frac{1}{3}+\boxed{?}=-\frac{1}{3}$

Do đó $\boxed{?}=-\frac{1}{3}-\frac{1}{3}=-\frac{2}{3}$;

∙ $-\frac{1}{3}+\boxed{?}=\frac{1}{3}$

Do đó $\boxed{?}=\frac{1}{3}-\left(-\frac{1}{3}\right)=\frac{1}{3}+\frac{1}{3}=\frac{2}{3}$;

Tương tự ta tính được các ô trống còn lại.

Ta điền các số vào tháp như sau:

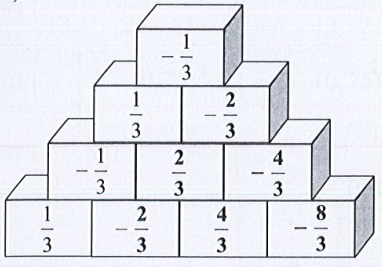
b) Áp dụng Quy tắc 2 thì tổng của hai ô trống bên dưới bằng ô phía trên liền với 2 ô đó.

Chẳng hạn ta tính:

∙ $-\frac{1}{2}.\boxed{?}=-\frac{1}{4}$

Do đó

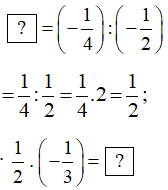
Do đó .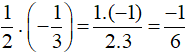

Tương tự ta tính được các ô trống còn lại.

Ta điền các số vào tháp như sau:

Bài 16 trang 14 Toán 7 tập 1: Một vệ tinh nhân tạo bay xung quanh Trái Đất ở độ cao 330 km so với mặt đất. Hỏi sau khi bay được đúng một vòng quanh Trái Đất thì vệ tinh đã bay được khoảng bao nhiêu ki-lô-mét? Biết rằng bán kính Trái Đất xấp xỉ 6 371 km (lấy π =3,14).

Lời giải:

Khi quanh xung quanh Trái Đất, vệ tinh nhân tạo di chuyển theo một đường tròn có bán kính khoảng:

6 371 + 330 = 6 701 (km).

Sau khi bay đúng một vòng Trái Đất thì vệ tinh bay được khoảng:

2 . 3,14 . 6 701 = 42 082,28 (km).

Vậy sau khi bay được đúng một vòng quanh Trái Đất thì vệ tinh đã bay được khoảng 42 082,28 ki-lô-mét.

Bài 17 trang 14 Toán 7 tập 1: Mẹ bạn Ngân gửi vào ngân hàng 20 triệu đồng với kì hạn 1 năm, lãi suất 7,8%/năm.

a) Tính số tiền cả gốc và lãi của mẹ bạn Ngân rút ra sau khi hết kì hạn 1 năm.

b) Sau kì hạn 1 năm, mẹ bạn Ngân rút ra $\frac{3}{40}$ số tiền (cả gốc và lãi) để mua một chiếc xe đạp thưởng cho bạn Ngân vì kết quả học tập đạt mức Tốt. Tính giá của chiếc xe đạp mà mẹ bạn Ngân đã mua.

Lời giải:

Mẹ bạn Ngân gửi vào ngân hàng 20 triệu đồng tức là mẹ bạn Ngân gửi vào ngân hàng 20 000 000 đồng.

a) Số tiền lãi mẹ bạn Ngân nhận được sau kì hạn 1 năm là:

20 000 000 . 7,8%  = 21 560 000 (đồng).

Vậy số tiền cả gốc và lãi của mẹ bạn Ngân rút ra sau khi hết kì hạn 1 năm là 21 560 000 đồng.

b) Giá của chiếc xe đạp mà mẹ bạn Ngân đã mua là:

$21560000.\frac{3}{40}=1617000$ (đồng).

Vậy giá của chiếc xe đạp mà mẹ bạn Ngân đã mua 1 617 000 đồng.

Bài 18 trang 14 Toán 7 tập 1: Một chiếc máy tính có giá niêm yết là 14 triệu đồng (đã bao gồm thuế VAT). Trong tuần lễ khai trương cửa hàng, chiếc máy tính đó được giảm giá 10% của giá niêm yết và nếu khách hàng mua hàng trực tuyến (giao hàng miễn phí) thì được giảm thêm 5% của giá niêm yết. Tính số tiền bác Lan phải trả khi mua hàng trực tuyến chiếc máy tính đó trong tuần lễ khai trương cửa hàng.

Lời giải:

Giá của chiếc máy tính khi mua hàng trực tuyến trong tuần lễ khai trương cửa hàng bằng:

100% − 10% − 5% = 85% (giá niêm yết).

Số tiền của bác Lan phải trả khi mua hàng trực tuyến chiếc máy tính đó trong tuần lễ khai trương cửa hàng là:

14 000 000 . 85% = 11 900 000 (đồng).

Vậy số tiền bác Lan phải trả khi mua hàng trực tuyến chiếc máy tính đó trong tuần lễ khai trương cửa hàng 11 900 000 đồng.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 1: Tập hợp Q các số hữu tỉ

Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

Bài 4: Thứ tự thực hiện phép tính. Quy tắc dấu ngoặc

Bài 5: Biểu diễn thập phân của số hữu tỉ

Lý thuyết Cộng, trừ, nhân, chia số hữu tỉ

1. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế

1.1 Quy tắc cộng, trừ hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

- Nếu hai số hữu tỉ cùng được viết dưới dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.

Ví dụ: Tính

a)  $0,5+\frac{-2}{3}$;                              

b) 1,205 – 2,31.

Hướng dẫn giải 

a) Ta có $0,5=\frac{5}{10}=\frac{1}{2}$ . Do đó:

$0,5+\frac{-2}{3}=\frac{1}{2}+\frac{-2}{3}=\frac{1.3}{2.3}+\frac{(-2).2}{3.2}\text{=}\frac{3}{6}+\frac{-4}{6}=\frac{3+(-4)}{6}=\frac{-1}{6}$.

b) 1,205 – 2,31= 1,205 + (–2,31) = – (2,31 – 1,205) = –1,105.

1.2 Tính chất của phép cộng các số hữu tỉ

- Phép cộng các số hữu tỉ có các tính chất giống với phép cộng các số nguyên: giao hoán, kết hợp, cộng với số 0, cộng với số đối.

- Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức chỉ có phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.

Ví dụ: Tính một cách hợp lý $(-0,4)+\frac{3}{8}+(-0,6)$

Ta có: $(-0,4)+\frac{3}{8}+(-0,6)=(-0,4)+(-0,6)+\frac{3}{8}=-1+\frac{3}{8}=\frac{-8}{8}+\frac{3}{8}=\frac{-5}{8}$

1.3 Quy tắc chuyển vế

Khi chuyển một số hạng tử vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:

x + y = z ⇒ x = z – y

x – y = z ⇒ x = z + y

Ví dụ: Tìm x, biết

a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$;                                                           

b) $\frac{15}{-2}-x=0,3$.

Hướng dẫn giải

a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$      

 $\text{x = }\left(-\frac{5}{6}\right)+\left(-\frac{7}{9}\right)$

 $\text{x =}\left(-\frac{15}{18}\right)+\left(-\frac{14}{18}\right)$

 $\text{ x = }-\frac{29}{18}$

Vậy $\text{ x = }-\frac{29}{18}$ .  

$b) \frac{15}{-2}-x=0,3$       

$\frac{15}{-2}-0,3=x$         

$\text{ x = }\frac{15}{-2}-0,3$

$\text{x = }-7,8$                 

Vậy x = – 7,8.

2. Nhân, chia hai số hữu tỉ

2.1 Quy tắc nhân, chia hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

- Nếu hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.

Ví dụ:

a) $2\frac{3}{8}:(-0,4)$ ;

b) $\frac{-12}{5}\cdot (-6,5)$ .

Hướng dẫn giải

a) Ta viết $2\frac{3}{8}=\frac{19}{8}$và $-0,4=\frac{-4}{10}=\frac{-2}{5}$

Khi đó: $2\frac{3}{8}:(-0,4)=\frac{19}{8}:\frac{-2}{5}=\frac{19}{8}\cdot \frac{5}{-2}=\frac{95}{-16}$

b) Ta có thể viết $-\frac{12}{5}=-\frac{24}{10}=-2,4$

Khi đó $\frac{-12}{5}\cdot (-6,5)=(-2,4).(-6,5)=15,6$ .

2.2 Tính chất của phép nhân các số hữu tỉ

Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.

Ví dụ: Tính một cách hợp lý:

a) $\frac{7}{3}\cdot (-2,5)\cdot \frac{6}{7}$ ;

b) $0,5\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)$ .

Hướng dẫn giải

a) $\frac{7}{3}\cdot (-2,5)\cdot \frac{6}{7}=\frac{7}{3}\cdot \frac{6}{7}\cdot (-2,5)=2\cdot (-2,5)=-5$

b) Ta có $0,5=\frac{5}{10}=\frac{1}{2}$ . Khi đó: 

$0,5\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)=\frac{1}{2}\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)=\frac{1}{2}\cdot \frac{2}{7}+\frac{1}{2}\cdot \frac{2}{-3}=\frac{1}{7}+\frac{1}{-3}=\frac{3}{21}+\frac{-7}{21}=\frac{-4}{21}$.

Nhận xét:

- Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là $\frac{1}{a}$ . Ta có $a.\frac{1}{a}=1$

- Số nghịch đảo của số hữu tỉ $\frac{1}{a}$ là a.

- Nếu a, b là hai số hữu tỉ và b ≠ 0 thì $a:b=a\cdot \frac{1}{b}$.

Ví dụ:

Số nghịch đảo của $\frac{-3}{5}$ là $1:\frac{-3}{5}=\frac{5}{-3}=\frac{-5}{3}$

Số nghịch đảo của 0,3 là $1:0,3=1:\frac{3}{10}=\frac{10}{3}$ .