Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 6: Cung chứa góc hay, chi tiết giúp học sinh dễ dàng làm bài tập Cung chứa góc lớp 9.
Giải bài tập Toán lớp 9 Bài 6: Cung chứa góc
Trả lời câu hỏi giữa bài
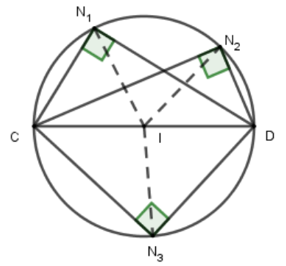
Câu hỏi 1 trang 84 SGK Toán lớp 9 Tập 2: Cho đoạn thẳng CD.
a) Vẽ ba điểm sao cho .
b) Chứng minh rằng các điểm nằm trên đường tròn đường kính CD.
Lời giải:
a)
b)
Gọi I là trung điểm của CD
Xét tam giác vuông tại ta có:
là đường trung tuyến ứng với cạnh huyền
(1)
Xét tam giác vuông tại ta có:
là đường trung tuyến ứng với cạnh huyền
Xét tam giác vuông tại ta có:
là đường trung tuyến ứng với cạnh huyền
Từ (1), (2) và (3) ta có:
Do đó, các điểm nằm trên đường tròn đường kính CD.
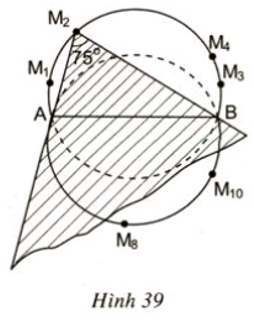
Dịch chuyển tấm bìa trong khe hở sao cho hai cạnh của góc luôn dính sát vào hai chiếc đinh A, B. Đánh dấu các vị trí của đỉnh góc .
Qua thực hành, hãy dự đoán quỹ đạo chuyển động của điểm M.
Lời giải:
Qua thực hành, dự đoán quỹ đạo chuyển động của điểm M là hai cung tròn đối xứng nhau qua dây AB.
Bài tập (trang 86)
Lời giải:
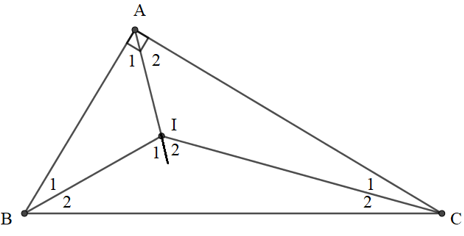
BI là tia phân giác của góc ABC
CI là tia phân giác của góc ACB
Mà do tam giác ABC vuông tại A
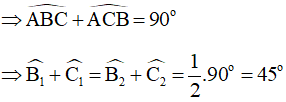
Ta có:
Góc là góc ngoài của tam giác ABI nên
Góc là góc ngoài của tam giác ACI nên ta có:
Do đó, Điểm I luôn nhìn đoạn thẳng BC dưới 1 góc không đổi là , vậy quỹ tích điểm I là cung chứa góc dựng trên đoạn thẳng BC.
Lời giải:
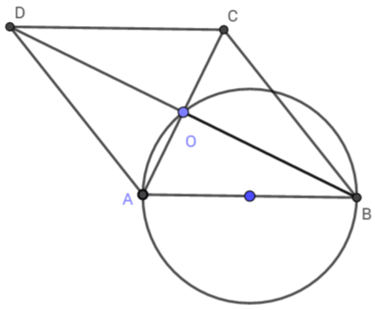
Theo giả thiết ta có: ABCD là hình thoi, có AC và BD là hai đường chéo
tại O (tính chất hình thoi)
Do đó, Điểm O luôn nhìn đoạn thẳng AB cố định dưới một góc không đổi là , vậy quỹ tích điểm O là đường tròn đường kính AB.
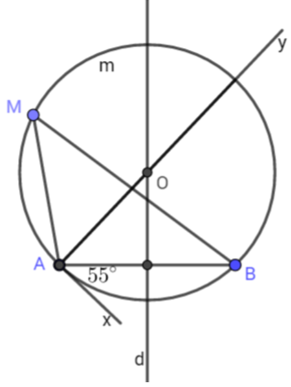
Bài 46 trang 86 SGK Toán lớp 9 Tập 2:Dựng một cung chứa góc trên đoạn thẳng AB = 3cm.
Lời giải:
Cách dựng:
- Dựng đoạn thẳng AB = 3cm
- Dựng góc
- Dựng tia Ay vuông góc với Ax
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chia khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta được cung AmB là cung chứa góc dựng trên đoạn AB = 3cm
Chứng minh:
Ta có:
O thuộc đường trung trực của AB (cách dựng) nên ta có: OA = OB
Do đó, B thuộc đường tròn (O; OA)
Có: tại A nên Ax là tiếp tuyến của (O; OA)
Do đó, góc BAx là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M thuộc cung AmB thì góc AMB là góc nội tiếp chắn cung nhỏ AB
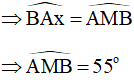
Do đó, cung AmB là cung chứa góc dựng trên đoạn AB = 3cm.

Lời giải:
a)
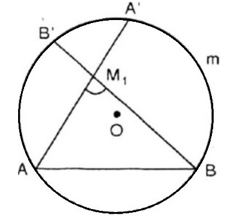
Điểm nằm bên trong cung chứa góc
Gọi B’, A’ lần lượt là giao điểm của và với cung tròn AmB.
Ta có: Góc AA’B là góc nội tiếp chắn cung nhỏ AB và cung AmB là cung chứa góc
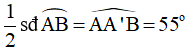
Vì là góc có đỉnh nằm trong đường tròn nên:
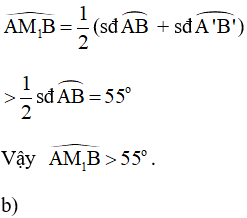
Điểm là điểm bất kì nằm ngoài đường tròn
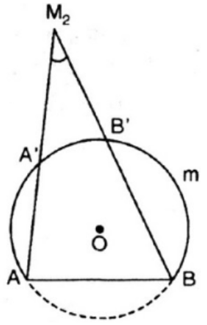
Ta có lần lượt cắt đường tròn tại A’, B’.
Ta có: Góc AA’B là góc nội tiếp chắn cung nhỏ AB và cung AmB là cung chứa góc
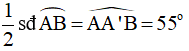
Vì là góc có đỉnh nằm bên ngoài đường tròn chắn cung A’B’ và AB nên ta có:
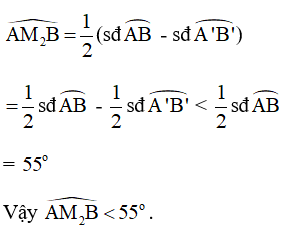
Luyện tập trang 87
Lời giải:
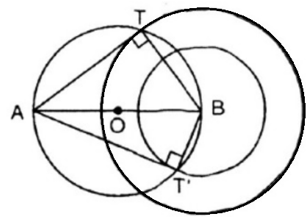
Phần thuận:
Ta có:
AT là tiếp tuyến của đường tròn (B; OT) với T là tiếp điểm
Do AB cố định nên quỹ tích của T là đường tròn đường kính AB.
Phần đảo:
Với T thuộc đường tròn đường kính AB

Do đó, AT tiếp xúc với đường tròn (B; BT < BA)
Kết luận: Quỹ tích các tiếp điểm là đường tròn đường kính AB.
Bài 49 trang 87 SGK Toán lớp 9 Tập 2:Dựng tam giác ABC, biết BC = 6cm, và đường cao AH = 4cm.
Lời giải:
Cách dựng:
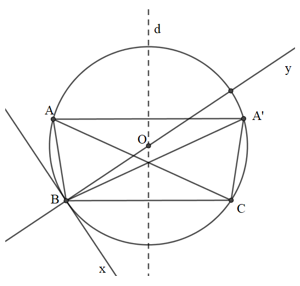
- Kẻ đoạn thẳng AB = 6cm
- Vẽ đường trung trực d của đoạn BC
- Vẽ tia Bx tạo với BC góc
- Vẽ tia By vuông góc với tia Bx tại B, tia By cắt đường thẳng d tại O.
- Vẽ cung BmC tâm O bán kính OB sao cho cung này nằm ở nửa mặt phẳng bờ BC không chứ Bx. Cung BmC chính là cung chứa góc cần dựng.
- Vẽ đường thẳng AA’ song song với BC và cách BC một khoảng 4cm, với A và A’ nằm trên cung BmC.
Khi đó, có hai tam giác thỏa mãn yêu cầu đề bài là tam giác ABC và tam giác A’BC.
Chứng minh:
Theo cách dựng ta có: BC = 6cm
Điểm A thuộc cung chứa góc dựng trên đoạn BC
AA’ // BC và cách BC 4cm nên chiều cao của tam giác ABC là 4cm
Vậy tam giác ABC thỏa mãn yêu cầu đề bài.
a) Chứng minh không đổi.
b) Tìm tập hợp các điểm I nói trên.
Lời giải:
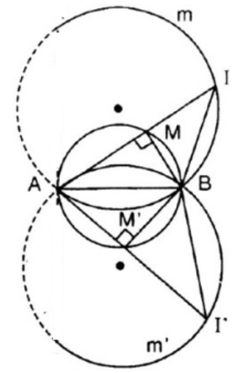
a)
Điểm M là điểm nằm trên đường tròn đường kính AB
là góc nội tiếp chắn nửa đường tròn
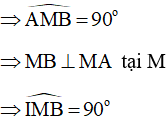
Do đó, tam giác IMB vuông tại I
Xét tam giác IMB vuông tại I
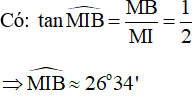
Vậy góc không đổi và luôn bằng .
b)
Vì không đổi và luôn bằng nên điểm I luôn nhìn đoạn AB cho trước một góc không đổi
Do đó, quỹ tích điểm I là cung chứa góc dựng trên đoạn AB.
Lời giải:
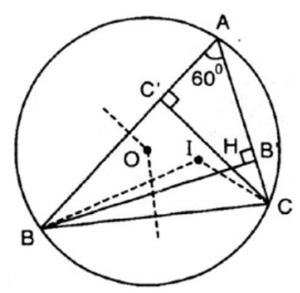
Ta có:
Góc BOC là góc ở tâm chắn cung nhỏ BC
![]()
Góc BAC là góc nội tiếp chắn cung nhỏ BC
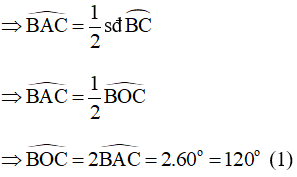
Xét tứ giác AC’HB’ có:
(tổng bốn góc trong một tứ giác)
Do BB'và CC' là các đường cao giao nhau tại H nên ta có:
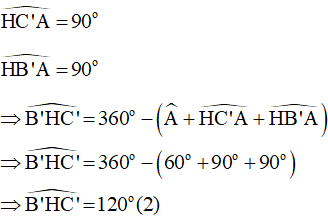
Xét tam giác IBC có:
BI là tia phân giác của góc ABC

Từ (1), (2) và (3) ta suy ra các điểm O, I, H nằm trên cung chứa góc dựng trên đoạn BC.
Vậy 5 điểm B, C, O, H, I nằm trên cùng 1 đường tròn.
Lời giải:
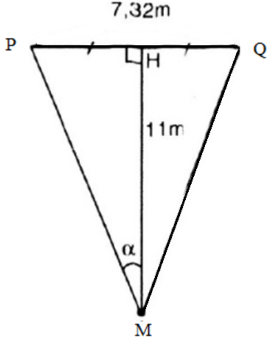
Dựng tam giác PMQ cân tại M.
Gọi chiều rộng cầu môn là PQ:
PQ = 7,32m
Gọi H là trung điểm của PQ
(m)
Lấy điểm M là điểm nằm trên đường trung trực của PQ sao cho MH = 11m
Do đó, M là vị trí đặt bóng cho quả sút phạt đền 11m
Xét tam giác PMQ cân tại M
MH là đường trung tuyến và cũng là đường cao
Do đó, tam giác MHP vuông tại H
Xét tam giác MHP vuông tại H có:
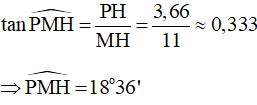
Xét tam giác PMQ cân tại M
MH là đường trung tuyến và cũng là đường phân giác.
Vậy góc sút phạt đền là:
Vẽ cung chứa góc dựng trên đoạn PQ. Bất cứ điểm nào trên cung vừa về cũng có "góc sút" như góc sút của quả phạt đền 11 mét.