Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong

Thanh Trà Ngày: 05-11-2022 Lớp 9

2.7 K

Với giải Bài 44 trang 86 Toán lớp 9 chi tiết trong Bài 6: Cung chứa góc giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 6: Cung chứa góc

Bài 44 trang 86 SGK Toán lớp 9 Tập 2: Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.

Lời giải:

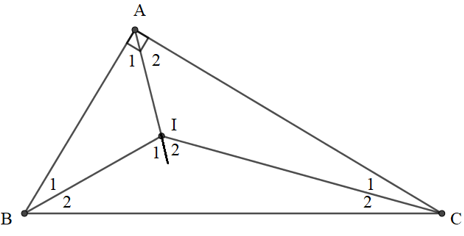
BI là tia phân giác của góc ABC $\Rightarrow \hat{B_{1}} = \hat{B_{2}} = \frac{1}{2} \hat{A B C}$

CI là tia phân giác của góc ACB $\Rightarrow \hat{C_{1}} = \hat{C_{2}} = \frac{1}{2} \hat{A C B}$

$\Rightarrow \hat{B_{1}} + \hat{C_{1}} = \hat{B_{2}} + \hat{C_{2}}$ $= \frac{1}{2} (\hat{A B C} + \hat{A C B})$

Mà do tam giác ABC vuông tại A

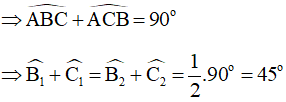
Tài liệu VietJack

Ta có:

Góc $I_{1}$ là góc ngoài của tam giác ABI nên $\hat{I_{1}} = \hat{A_{1}} + \hat{B_{1}}$

Góc $I_{2}$ là góc ngoài của tam giác ACI nên ta có: $\hat{I_{2}} = \hat{A_{2}} + \hat{C_{1}}$

$\Rightarrow \hat{I_{2}} + \hat{I_{2}} = \hat{A_{1}} + \hat{B_{1}} + \hat{A_{2}} + \hat{C_{1}} \Rightarrow \hat{B I C} = \hat{A_{1}} + \hat{A_{2}} + \hat{B_{1}} + \hat{C_{1}} = 90^{o} + 45^{o} = 135^{o}$