Với giải Bài 51 trang 87 Toán lớp 9 chi tiết trong Bài 6: Cung chứa góc giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 6: Cung chứa góc
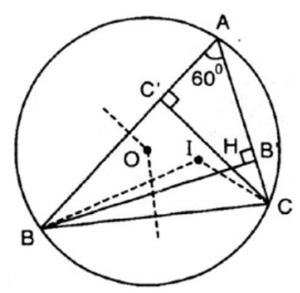
Bài 51 trang 87 SGK Toán lớp 9 Tập 2:Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với . Gọi H là giao điểm của các đường cao BB'và CC'. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
Lời giải:
Ta có:
Góc BOC là góc ở tâm chắn cung nhỏ BC
Góc BAC là góc nội tiếp chắn cung nhỏ BC
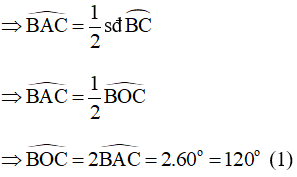
Xét tứ giác AC’HB’ có:
(tổng bốn góc trong một tứ giác)
Do BB'và CC' là các đường cao giao nhau tại H nên ta có:
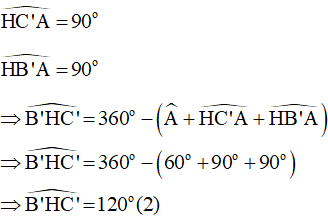
Xét tam giác IBC có:
BI là tia phân giác của góc ABC
Từ (1), (2) và (3) ta suy ra các điểm O, I, H nằm trên cung chứa góc dựng trên đoạn BC.
Vậy 5 điểm B, C, O, H, I nằm trên cùng 1 đường tròn.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
