Giải SGK Toán 9 Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số

Admin Vietjack Ngày: 21-10-2022 Lớp 9
2 K
2 K

Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số hay, chi tiết giúp học sinh dễ dàng làm bài tập Giải hệ phương trình bằng phương pháp cộng đại số lớp 9.

Giải bài tập Toán lớp 9 Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 17 Toán 9 Tập 2: Áp dụng quy tắc cộng đại số để biến đổi hệ (I), nhưng ở bước 1, hãy trừ từng vế hai phương trình của hệ (I) và viết ra các hệ phương trình mới thu được.

(I) 2x−y=1x+y=2

Lời giải

(I) 2x−y=1x+y=2

Trừ từng vế hai phương trình của hệ (I) ta được phương trình:

(2x – y) – (x + y) = 1 – 2

⇔2x−y−x−y=−1

 ⇔ x – 2y = -1

Khi đó, ta thu được hệ phương trình mới:

x−2y=−1x+y=2 hoặc 2x−y=1x−2y=−1

Câu hỏi 2 trang 17 Toán 9 Tập 2: Các hệ số của y trong hai phương trình của hệ (II) có đặc điểm gì ?

(II) 2x+y=3x−y=6

Lời giải

Hệ số của y trong hai phương trình của hệ (II) đối nhau (có tổng bằng 0)

Câu hỏi 3 trang 18 Toán 9 Tập 2: a) Nêu nhận xét về các hệ số của x trong hai phương trình của hệ (III).

b) Áp dụng quy tắc cộng đại số, hãy giải hệ (III) bằng cách trừ từng vế hai phương trình của (III).

Lời giải

a) Hệ số của x trong hai phương trình của hệ (III) giống nhau

b) (III) 2x+2y=92x−3y=4

Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được:

(2x + 2y ) – (2x – 3y) = 9 – 4

⇔2x + 2y – 2x + 3y = 5

⇔5y = 5

Do đó:

(III)⇔5y=52x−3y=4⇔y=5:52x−3y=4⇔y=12.x−3.1=4⇔2x=4+3y=1⇔2x=7y=1⇔x=72y=1

Vậy hệ phương trình có nghiệm duy nhất 72;1

Câu hỏi 4 trang 18 Toán 9 Tập 2: Giải tiếp hệ (IV) bằng phương pháp đã nêu ở trường hợp thứ nhất.

(IV)3x+2y=72x+3y=3

Lời giải

(IV)⇔6x+4y=146x+9y=9

Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được:

(6x + 4y) – (6x + 9y) = 14 – 9

⇔6x+4y−6x−9y=5⇔−5y=5

⇔-5y = 5

Do đó:

(IV)⇔−5y=52x+3y=3⇔y=−12x+3.(−1)=3⇔2x−3=3y=−1⇔2x=6y=−1⇔x=3y=−1

Vậy hệ phương trình đã cho có nghiệm(x; y) = (3; -1).

Bài tập (trang 19)

Bài 20 trang 19 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a) 3x+y=32x−y=7

b) 2x+5y=82x−3y=0

c) 4x+3y=62x+y=4

d) 2x+3y=−23x−2y=−3

e) 0,3x+0,5y=31,5x−2y=1,5

Lời giải:

a)3x+y=32x−y=7⇔3x+y+2x−y=3+72x−y=7

 (cộng vế với vế của hai phương trình)

⇔5x=102x−y=7⇔x=10:52x−y=7⇔x=22.2−y=7⇔x=2y=4−7=−3

Vậy hệ phương trình đã cho có nghiệm (x; y) = (2; -3).

b)2x+5y=82x−3y=0

⇔2x+5y−2x−3y=8−02x−3y=0 (trừ vế với vế của phương trình thứ nhất cho phương trình thứ hai)

⇔2x+5y−2x+3y=82x−3y=0⇔8y=82x−3y=0⇔y=8:82x−3y=0⇔2x−3.1=0y=1⇔2x−3=0y=1⇔2x=3y=1⇔x=32y=1

Vậy hệ phương trình đã cho có nghiệm (x; y) = 32;1.

c)4x+3y=62x+y=4⇔4x+3y=64x+2y=8

 (nhân cả hai vế phương trình thứ hai với 2)

⇔4x+3y=64x+3y−4x+2y=6−8 (Trừ vế với vế của phương trình thứ nhất cho phương trình thứ hai)

⇔4x+3y=64x+3y−4x−2y=−2⇔4x+3y=6y=−2⇔4x+3.(−2)=6y=−2⇔4x=6+6y=−2⇔4x=12y=−2⇔x=3y=−2

Vậy hệ phương trình đã cho có nghiệm (x; y) = (3; -2).

d)2x+3y=−23x−2y=−3⇔6x+9y=−66x−4y=−6

 (Ta nhân cả hai vế của phương trình một với 3 và phương trình hai với 2)

⇔6x+9y=−66x+9y−6x−4y=(−6)−(−6) (trừ vế với vế của phương thứ nhất cho phương trình thứ hai)

⇔6x+9y=−66x+9y−6x+4y=0⇔6x+9y=−613y=0⇔6x+9y=−6y=0⇔6x+9.0=−6y=0⇔6x=−6y=0⇔x=−1y=0

Vậy hệ phương trình đã cho có nghiệm (x; y) = (-1; 0).

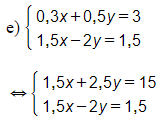
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3x + y = 3 và 2x - y = 7 (ảnh 1)

(Ta nhân cả hai vế của phương trình thứ nhất với 5)

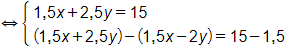
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3x + y = 3 và 2x - y = 7 (ảnh 1) 

(trừ vế với vế của phương thứ nhất cho phương trình thứ hai)

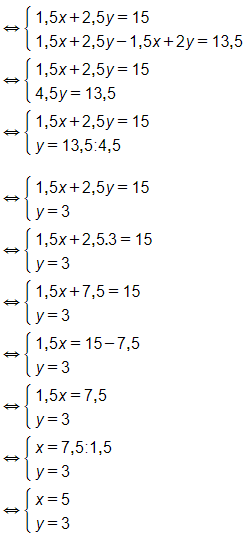
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3x + y = 3 và 2x - y = 7 (ảnh 1)

Vậy hệ phương trình đã cho có nghiệm (x; y) = (5; 3)

Bài 21 trang 19 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a) x2−3y=12x+y2=−2

b) 5x3+y=22x6−y2=2

Lời giải:

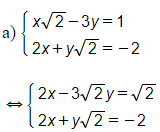
Giải các hệ phương trình sau bằng phương pháp cộng đại số: x căn 2 - 3y = 1 (ảnh 1)

(nhân của hai vế phương trình thứ nhất với )

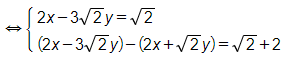Giải các hệ phương trình sau bằng phương pháp cộng đại số: x căn 2 - 3y = 1 (ảnh 1) (trừ vế với vế của phương trình thứ nhất với phương trình thứ hai).

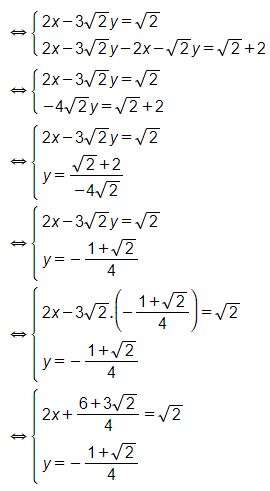
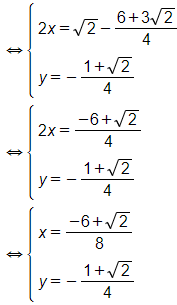
Giải các hệ phương trình sau bằng phương pháp cộng đại số: x căn 2 - 3y = 1 (ảnh 1)

Giải các hệ phương trình sau bằng phương pháp cộng đại số: x căn 2 - 3y = 1 (ảnh 1)

Vậy hệ phương trình có nghiệm (x;y) = (-6 +28;-1+24)

b)

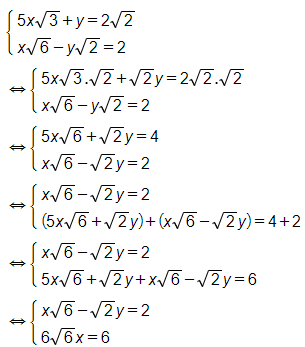
 Giải các hệ phương trình sau bằng phương pháp cộng đại số: x căn 2 - 3y = 1 (ảnh 1)

⇔x6−2y=2x=6:66⇔x6−2y=2x=66⇔x=666.66−2y=2⇔x=661−2y=2⇔x=662y=−1⇔x=66y=−22

Vậy hệ phương trình đã cho có nghiệm (x; y) = 66;−22.

Luyện tập trang 19, 20

Bài 22 trang 19 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a) −5x+2y=46x−3y=−7

b) 2x−3y=11−4x+6y=5

c) 3x−2y=10x−23y=313

Lời giải:

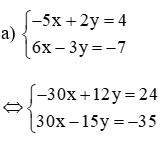
Giải các hệ phương trình sau bằng phương pháp cộng đại số: -5x + 2y =4 (ảnh 1) 

(Nhân cả hai vế phương trình thứ nhất với 6 và phương trình thứ hai với 5)

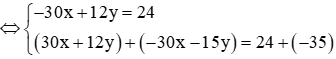
Giải các hệ phương trình sau bằng phương pháp cộng đại số: -5x + 2y =4 (ảnh 1)

(cộng vế với vế của hai phương trình)

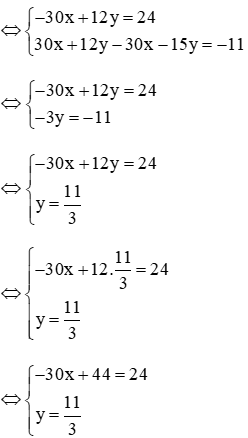
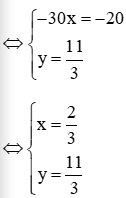
Giải các hệ phương trình sau bằng phương pháp cộng đại số: -5x + 2y =4 (ảnh 1)

Giải các hệ phương trình sau bằng phương pháp cộng đại số: -5x + 2y =4 (ảnh 1)

Vậy hệ phương trình đã cho nghiệm (x; y) =23;113.

b)

2x−3y=11−4x+6y=5

⇔4x−6y=22−4x+6y=5 (Nhân cả hai vế phương trình thứ nhất với 2)

⇔4x−6y=224x−6y+−4x+6y=22+5 (cộng vế với vế của hai phương trình)

⇔4x−6y=224x−6y−4x+6y=27⇔4x−6y=220=27 vô lí

Vậy hệ phương trình đã cho vô nghiệm.

c) 3x−2y=10x−23y=313

⇔3x−2y=103x−3.23y=103.3 (nhân cả hai vế phương trình thứ hai với 3)

⇔3x−2y=103x−2y=10

⇔3x−2y−3x−2y=10−103x−2y=10(trừ vế với vế của phương thứ nhất cho phương trình thứ hai)

⇔0=03x−2y=10

Vậy hệ phương trình đã cho có vô số nghiệm và tập nghiệm của nó là tập hớp các điểm nằm trên đường thẳng 3x – 2y = 10.

Bài 23 trang 19 SGK Toán 9 Tập 2: Giải hệ phương trình sau:

1+2x+1−2y=51+2x+1+2y=3

Lời giải:

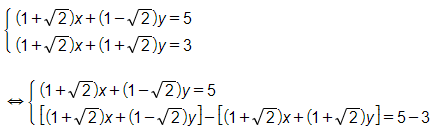
Giải hệ phương trình sau: (1 + căn 2).x + (1 - căn 2).y = 5 và (1 + căn 2).x + (1 + căn 2).y = 3 (ảnh 1)

(trừ vế với vế của phương thứ nhất cho phương trình thứ hai)

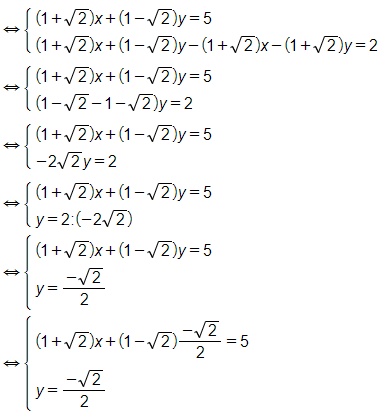
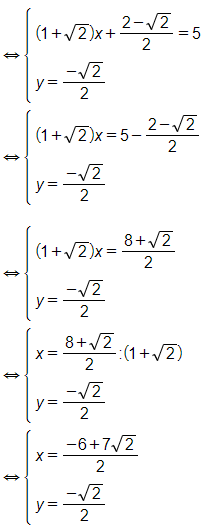
Giải hệ phương trình sau: (1 + căn 2).x + (1 - căn 2).y = 5 và (1 + căn 2).x + (1 + căn 2).y = 3 (ảnh 1)

Giải hệ phương trình sau: (1 + căn 2).x + (1 - căn 2).y = 5 và (1 + căn 2).x + (1 + căn 2).y = 3 (ảnh 1)

Vậy hệ phương trình đã cho có nghiệm (x; y) =−6+722;−22.

Bài 24 trang 19 SGK Toán 9 Tập 2: Giải các hệ phương trình sau:

a) 2x+y+3x−y=4x+y+2x−y=5

b) 2x−2+31+y=−23x−2−21+y=−3

Lời giải:

a)

2x+y+3x−y=4x+y+2x−y=5⇔2x+2y+3x−3y=4x+y+2x−2y=5

⇔5x−y=43x−y=5⇔5x−y=45x−y−3x−y=4−5

(trừ vế với vế của phương thứ nhất cho phương trình thứ hai)

⇔5x−y=45x−y−3x+y=−1⇔5x−y=42x=−1⇔x=−125.−12−y=4⇔x=−12−52−y=4⇔x=−12y=−52−4⇔x=−12y=−132

Vậy hệ phương trình có nghiệm (x;y) = (-12; -132)

b)

2x−2+31+y=−23x−2−21+y=−3⇔2x−4+3+3y=−23x−6−2−2y=−3⇔2x+3y−1=−23x−2y−8=−3⇔2x+3y=−2+13x−2y=−3+8⇔2x+3y=−13x−2y=5

⇔6x+9y=−36x−4y=10(Nhân cả hai vế phương trình thứ nhất với 3 và phương trình thứ hai với hai)

⇔6x+9y=−36x+9y−6x−4y=−3−10⇔6x+9y=−36x+9y−6x+4y=−13⇔6x+9y=−313y=−13⇔6x+9.(−1)=−3y=−1

⇔6x−9=−3y=−1⇔6x=−3+9y=−1⇔6x=6y=−1⇔x=1y=−1

Vậy hệ phương trình đã cho có nghiệm (x; y) = (1; -1).

Bài 25 trang 19 SGK Toán 9 Tập 2: Ta biết rằng: Một đa thức bằng đa thức 0 khi và chỉ khi tất cả các hệ số của nó bằng 0. Hãy tìm các giá trị của m và n để đa thức sau (với biến số x) bằng đa thức 0:

P(x) = (3m - 5n +1)x + (4m - n - 10)

Lời giải

Đa thức P(x) bằng đa thức 0 khi và chỉ khi:

3m−5n+1=04m−n−10=0

⇔3m−5n=−14m−n=10

⇔3m−5n=−120m−5n=50(nhân cả hai vế phương trình thứ hai với 5)

⇔3m−5n=−13m−5n−20m−5n=−1−50⇔3m−5n=−13m−5n−20m+5n=−51⇔3m−5n=−1−17m=−51⇔3m−5n=−1m=−51:−17⇔m=33.3−5.n=−1⇔m=39−5n=−1⇔m=35n=10⇔m=3n=2

Vậy m = 3 và n = 2 thì đa thức P(x) bằng đa thứ 0.

Bài 26 trang 19 SGK Toán 9 Tập 2: Xác định a và b để đồ thị của hàm số y = ax + b đi qua hai điểm A và B trong mỗi trường hợp sau:

a) A(2; -2) và B(-1; 3) ;    

b) A(-4; -2) và B(2; 1)

c) A(3; -1) và B(-3; 2) ;    

d) A và B(0; 2)

Lời giải

a) Đồ thị hàm số y = ax + b đi qua A(2; -2). Thay x = 2 và y = -2 vào hàm số ta có:

2.a + b = -2 (1)

Đồ thị hàm số y = ax + b đi qua B(-1 ; 3). Thay x = -1; y = 3 vào hàm số ta có:

a.(-1) + b = 3 (2)

Từ (1) và (2) ta có hệ phương trình :

2a+b=−2−a+b=3⇔2a+b=−22a+b−−a+b=−2−3⇔2a+b=−22a+b+a−b=−5⇔2a+b=−23a=−5⇔2a+b=−2a=−5:3⇔a=−532.−53+b=−2⇔a=−53−103+b=−2⇔a=−53b=−2+103⇔a=−53b=43

Vậy a =-53; b = 43.

b) Đồ thị hàm số y = ax + b đi qua A(-4; -2). Thay x = -4; y = -2 vào hàm số ta được:

 a.(-4) + b = -2 (3)

Đồ thị hàm số y = ax + b đi qua B(2 ; 1). Thay x = 2 ; y = 1 vào hàm số ta được:

a.2 + b = 1 (4)

Từ (3) và (4) ta có hệ phương trình:

−4a+b=−22a+b=1⇔−4a+b−2a+b=−2−12a+b=1⇔−4a+b−2a−b=−32a+b=1⇔−6a=−32a+b=1⇔a=122.12+b=1⇔a=121+b=1⇔a=12b=0

Vậy a = 12 và b = 0

c) Đồ thị hàm số y = ax + b đi qua A(3 ; -1). Thay x = 3 và y = -1 vào hàm số ta được:

a.3 + b = -1 (5)

Đồ thị hàm số y = ax + b đi qua B(-3 ; 2). Thay x = -3; y = 2 vào hàm số ta được:

a.(-3) + b = 2 (6)

Ta có hệ phương trình :

Từ (5) và (6) ta có hệ phương trình:

3a+b=−1−3a+b=2⇔3a+b=−13a+b+−3a+b=−1+2⇔3a+b=−13a+b−3a+b=1⇔3a+b=−12b=1⇔3a+12=−1b=12⇔3a=−1−12b=12⇔3a=−32b=12⇔a=−32:3b=12⇔a=−12b=12

Vậy a=−12;b=12

d) Đồ thị hàm số y = ax + b đi qua A 3;2.Thay x =3; y = 2 ta có:

a. 3 + b = 2 (*)

Đồ thị hàm số y = ax + b đi qua B(0; 2). Thay x = 0 và y = 2 ta có:

a.0 + b = 2 ⇔ b = 2.

Thay b = 2 vào (*) ta được:

a. 3 + 2 = 2 ⇔ a. 3 = 0 ⇔ a = 0.

Vậy a = 0 và b = 2.

Bài 27 trang 20 SGK Toán 9 Tập 2: Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:

a) 1x−1y=13x+4y=5

Hướng dẫn: Đặt u = 1x;v=1y

b)  1x−2+1y−1=22x−2−3y−1=1

Hứng dẫn: Đặt u=1x−2;v=1y−1

Lời giải:

a) 1x−1y=13x+4y=5 (I)

Đặt 1x=u1y=v. Hệ phương trình (I) trở thành u−v=13u+4v=5

⇔3u−3v=33u+4v=5⇔u−v=13u−3v−3u+4v=3−5⇔u−v=13u−3v−3u−4v=−2⇔u−v=1−7v=−2⇔u=1+vv=27⇔u=1+27v=27⇔u=97v=27⇒1x=971y=27⇔x=79y=72

Vậy hệ phương trình có nghiệm (x; y) =79;72

b) 1x−2+1y−1=22x−2−3y−1=1(II)

Đặt 1x−2=u1y−1=v. Khi đó hệ (II) trở thành u+v=22u−3v=1

⇔2u+2v=42u−3v=1⇔u+v=22u+2v−2u−3v=4−1⇔u+v=22u+2v−2u+3v=3⇔u+v=25v=3⇔u+v=2v=35⇔u+35=2v=35⇔u=2−35v=35⇔u=75v=35⇔1x−2=751y−1=35⇔7x−2=53y−1=5⇔7x−14=53y−3=5⇔7x=14+53y=5+3⇔7x=193y=8⇔x=197y=83

Vậy hệ phương trình đã cho có nghiệm (x; y) = 197;83.

Từ khóa :
Giải hệ phương trình bằng phương pháp cộng đại số toán 9 Giải bài tập
Đánh giá

0

0 đánh giá

Đánh giá
Bài viết cùng môn học
Toán Tổng hợp kiến thức
Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6
Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My
164
Toán Tổng hợp kiến thức
Tìm các tập hợp Ư(8); Ư(12); Ư(15)
Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My
141
Toán Tổng hợp kiến thức
Tìm BCNN của 84 và 108
Tìm BCNN của 84 và 108 Lữ Ngọc My My
115
Toán Tổng hợp kiến thức
Cho biết cos∝ = 12/13 giá trị của tan ∝ là
Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My
110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.

DMCA.com Protection Status