Giải SGK Toán 7 Bài 16 (Kết nối tri thức): Tam giác cân. Đường trung trực của đoạn thẳng

Nguyễn Linh Anh Ngày: 26-08-2024 Lớp 7

12.8 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng chi tiết sách Toán 7 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Video bài giảng Tam giác cân. Đường trung trực của đoạn thẳng - Kết nối tri thức

Giải Toán 7 trang 80 Tập 1

1. Tam giác cân và tính chất

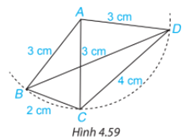
Câu hỏi trang 80 Toán lớp 7: Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.

Phương pháp giải:

Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau đó gọi là 2 cạnh bên, cạnh còn lại của tam giác gọi là cạnh đáy.

Lời giải:

+) Tam giác ABD cân tại đỉnh A có:

AB, AD là 2 cạnh bên

BD là cạnh đáy

$\hat{B}, \hat{D}$ là 2 góc ở đáy

$\hat{A}$ là góc ở đỉnh

+) Tam giác ADC cân tại A có:

AC, AD là 2 cạnh bên

DC là cạnh đáy

$\hat{C}, \hat{D}$ là 2 góc ở đáy

$\hat{A}$ là góc ở đỉnh

+) Tam giác ABC cân tại A có:

AB, AC là 2 cạnh bên

BC là cạnh đáy

$\hat{C}, \hat{B}$ là 2 góc ở đáy

$\hat{A}$ là góc ở đỉnh

Giải Toán 7 trang 81 Tập 1

HĐ 1 trang 81 Toán lớp 7: Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.

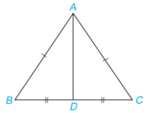
a) Chứng minh rằng $Δ$ ABD = $Δ$ ACD theo trường hợp cạnh - cạnh - cạnh.

b) Hai góc B và C của tam giác ABC có bằng nhau không?

Phương pháp giải:

a) Chứng minh ba cạnh của 2 tam giác trên bằng nhau

b) Từ câu a) suy ra 2 cặp góc tương ứng bằng nhau.

Lời giải:

a) Xét hai tam giác ABD và ACD có:

AB=AC (do tam giác ABC cân tại A).

AD chung

BD=DC (do D là trung điểm của đoạn thẳng BC).

=> $Δ$ ABD = $Δ$ ACD (c.c.c)

b) Do $Δ$ ABD = $Δ$ ACD nên $\hat{B} = \hat{C}$ ( 2 góc tương ứng)

HĐ 2 trang 81 Toán lớp 7: Cho tam giác MNP có $\hat{M} = \hat{N}$ . Vẽ tia phân giác PK của góc MPN (K $\in$ MN).

Chứng minh rằng:

a) $\hat{M K P} = \hat{N K P}$ ;

b) $Δ M P K = Δ N P K$ ;

c) Tam giác MNP có cân tại P không?

Phương pháp giải:

a) Sử dụng định lí: Tổng 3 góc trong một tam giác bằng 180 độ

b) Chứng minh 2 tam giác bằng nhau theo trường hợp góc – cạnh - góc

c) Sử dụng định nghĩa tam giác cân: Tam giác MNP cân là tam giác có 2 cạnh bằng nhau

Lời giải:

Xét tam giác MPK có:

$\hat{P K M} + \hat{M P K} + \hat{K M P} = 180^{o}$

Xét tam giác NPK có:

$\hat{P K N} + \hat{N P K} + \hat{K N P} = 180^{o}$

Mà $\hat{KMP} = \hat{KNP} (theo giả thiết); \hat{MPK} = \hat{NPK} (do PK là tia phân giác của \hat{MPN})$

Suy ra $\hat{M K P} = \hat{N K P}$ .

b)Xét hai tam giác MPK và NPK có:

$\hat{M K P} = \hat{N K P}$ (do PK là tia phân giác của góc MPN).

PK chung

$\hat{M K P} = \hat{N K P}$ (chứng minh trên).

=> $Δ M P K = Δ N P K$ (g.c.g)

c) Do $Δ M P K = Δ N P K$ nên MP=NP (2 cạnh tương ứng)

Suy ra tam giác MNP cân tại P.

Luyện tập 1 trang 81 Toán lớp 7: Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.

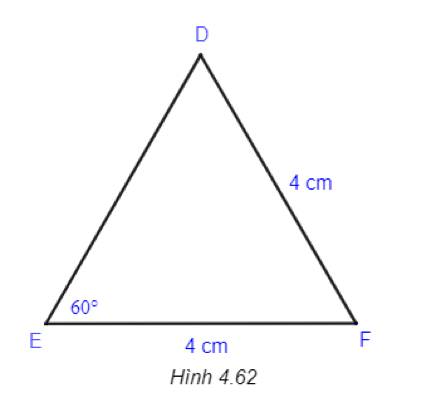
Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng | Kết nối tri thức (ảnh 1)

Phương pháp giải:

Chứng minh tam giác DEF cân tại F từ đó suy ra số đo các góc.

Lời giải:

Xét tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.

Suy ra $\hat{F E D} = \hat{F D E} = 60^{o}$ ( tính chất tam giác cân)

Áp dụng định lí tổng ba góc trong tam giác vào tam giác DEF, ta có:

$\begin{array}{l} \hat{F D E} + \hat{F E D} + \hat{D F E} = 180^{o} \\ \Rightarrow 60^{o} + 60^{o} + \hat{D F E} = 180^{o} \\ \Rightarrow \hat{D F E} = 60^{o} \end{array}$

Thử thách nhỏ trang 81 Toán lớp 7: Một tam giác có gì đặc biệt nếu thoả mãn một trong các điều kiện sau:

a) Tam giác có ba góc bằng nhau?

b) Tam giác cân có một góc bằng 60°?

Phương pháp giải:

Áp dụng: Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc ba góc bằng nhau.

Lời giải:

a) Tam giác có ba góc bằng nhau là tam giác đều

b) Tam giác cân có 1 góc bằng 60 độ là tam giác đều.

2. Đường trung trực của một đoạn thẳng

HĐ 3 trang 81 Toán lớp 7: Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB. Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp.

a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?

b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?

Phương pháp giải:

Dùng thước đo kiểm tra.

Lời giải:

a) O có là trung điểm của đoạn thẳng AB

b) Dùng thước đo góc ta thấy d có vuông góc với AB.

Giải Toán 7 trang 82 Tập 1

Câu hỏi trang 82 Toán lớp 7: Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng?

Phương pháp giải:

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó

Lời giải:

Do: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó

Nên hình a) Lan vẽ đúng.

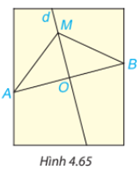
HĐ 4 trang 82 Toán lớp 7: Trên mảnh giấy trong HĐ3, lấy điểm M bất kì trên đường thẳng d. Dùng thước thẳng có vạch chia kiểm tra xem AM có bằng BM không (H.4.65).

Phương pháp giải:

Dùng thước kiểm tra

Lời giải:

Lấy điểm M bất kì trên đường thẳng d dùng thước kiểm tra ta thấy AM bằng BM.

Giải Toán 7 trang 83 Tập 1

Luyện tập 2 trang 83 Toán lớp 7: Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và $\hat{M A B}$ = 60° (H.4.67). Tính BM và số đo góc MBA.

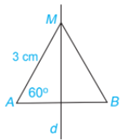
Phương pháp giải:

Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

Lời giải:

Vì M là một điểm nằm trên đường trung trực của đoạn thẳng AB nên MA=MB=3cm.

$\Rightarrow$ Tam giác MAB cân tại M.

$\Rightarrow$ $\hat{M A B} = \hat{M B A} = 60^{o}$ .

Giải Toán 7 trang 84 Tập 1

Bài tập

Bài 4.23 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.

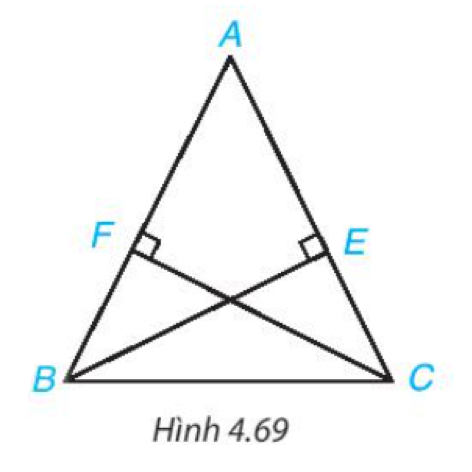
Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng | Kết nối tri thức (ảnh 2)

Phương pháp giải:

Chứng minh 2 tam giác bằng nhau để suy ra 2 cạnh tương ứng bằng nhau

Lời giải:

Do tam giác ABC cân tại A nên: $\hat{A B C} = \hat{A C B}$ (tính chất tam giác cân)

Xét 2 tam giác vuông BFC và CEB:

$\hat{A B C} = \hat{A C B}$

BC chung

=> $Δ B F C = Δ C E B$ (cạnh huyền – góc nhọn)

=>BE=CF (2 cạnh tương ứng).

Bài 4.24 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.

Phương pháp giải:

Chứng minh 2 tam giác AMC và AMB bằng nhau từ đó suy ra các cặp góc tương ứng bằng nhau.

Lời giải:

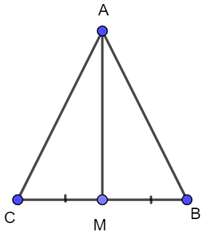
Xét 2 tam giác AMC và AMB có:

AM chung

AB=AC (do tam giác ABC cân tại A)

MB=MC (gt)

$\Rightarrow$ $Δ$ AMB=AMC(c.c.c)

$\Rightarrow$ $\hat{C A M} = \hat{C B M}$ (2 góc tương ứng)

$\Rightarrow$ AM là phân giác của góc BAC

Mặt khác: $\hat{A M B} = \hat{A M C}$ (2 góc tương ứng) mà $\hat{A M B} + \hat{A M C} = 180^{o}$ ( 2 góc kề bù)

Nên: $\hat{A M B} = \hat{A M C} = 90^{o}$ .

Vậy AM vuông góc với BC.

Bài 4.25 trang 84 Toán lớp 7: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.

a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.

b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.

Phương pháp giải:

a) Chứng minh tam giác hai tam giác AMB và AMC bằng nhau $\Rightarrow$ Tam giác ABC cân.

b) Từ M kẻ hai đường vuông góc với AC và AB từ đó chứng minh hai góc B và C bằng nhau.

$\Rightarrow$ Chứng minh hai tam giác AMB và AMC bằng nhau

$\Rightarrow$ Tam giác ABC cân

Lời giải:

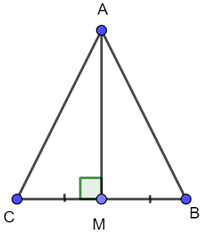
Xét 2 tam giác vuông AMC và AMB có:

AM chung

BM=CM (gt)

=> $Δ A M B = Δ A M C$ (c.g.c)

=> AM=BM (2 cạnh tương ứng)

=> Tam giác ABM cân tại A

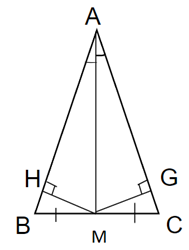
Kẻ MH vuông góc với AB(H thuộc AB)

MG vuông góc với AC (G thuộc AC)

Xét 2 tam giác vuông AHM và AGC có:

$\hat{H A M} = \hat{G A M}$

AM chung

=> $Δ A H M = Δ A G C$ (cạnh huyền – góc nhọn)

=>HM=GM (2 cạnh tương ứng)

Xét 2 tam giác vuông BHM và CGM có:

BM=CM(gt)

MH=MG(cmt)

=> $Δ B H M = Δ C G M$ (cạnh huyền – cạnh góc vuông)

=> $\hat{B M H} = \hat{C M H}$ (2 góc tương ứng)

=>Tam giác ABC cân tại A.

Bài 4.26 trang 84 Toán lớp 7: Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân. Hãy giải thích các khẳng định sau:

a) Tam giác vuông cân thì cân tại đỉnh góc vuông;

b) Tam giác vuông cân có hai góc nhọn bằng 45°;

c) Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.

Phương pháp giải:

Áp dụng tổng ba góc trong tam giác bằng 180 độ.

Lời giải:

a)Do tổng ba góc trong 1 tam giác bằng 180 độ nên tam giác không thể có 2 góc vuông

=>Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau

=> Tam giác vuông cân thì cân tại đỉnh góc vuông.

b) Giả sử hai góc nhọn trong tam giác vuông là x, ta có:

$\begin{array}{l} x + x + 90^{o} = 180^{o} \\ \Rightarrow 2 x = 90^{o} \\ \Rightarrow x = 45^{o} \end{array}$

Vậy tam giác vuông cân có hai góc nhọn bằng 45°.

a) Gọi góc còn lại của tam giác vuông có 1 góc nhọn bằng 45° là x, ta có:

$x + 45^{o} + 90^{o} = 180^{o} \Rightarrow x = 45^{o}$

Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.

Bài 4.27 trang 84 Toán lớp 7: Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB?

Phương pháp giải:

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

Lời giải:

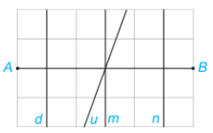
Quan sát hình 4.70 ta thấy đường thẳng m vuông góc với đoạn thẳng AB tại trung điểm của AB nên m là đường trung trực của AB.

Bài 4.28 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC.

Phương pháp giải:

Chứng minh 2 tam giác bằng nhau suy ra 2 cạnh tương ứng bằng nhau, 2 góc tương ứng bằng nhau

Chú ý: Hai góc kề bù bằng nhau thì mỗi góc bằng 90 độ

Lời giải:

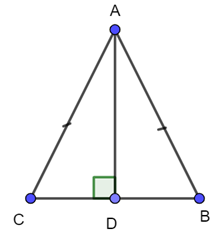
Do tam giác ABC cân tại A nên AB = AC, $\hat{ABC} = \hat{ACB} hay \hat{ABD} = \hat{ACD}$

Do AD là đường cao của tam giác ABC hay AD ⊥ BC tại D nên tam giác ABD vuông tại D và tam giác ACD vuông tại D.

Xét hai tam giác ABD vuông tại D và tam giác ACD vuông tại D có:

AB = AC (chứng minh trên).

$\hat{ABD} = \hat{ACD}$ (chứng minh trên).

Do đó $∆ ABD = ∆ ACD$ (cạnh huyền – góc nhọn).

Khi đó BD = CD (2 cạnh tương ứng) hay D là trung điểm của đoạn thẳng BC.

Do AD vuông góc với BC tại trung điểm của BC nên AD là đường trung trực của đoạn thẳng BC.

Vậy đường thẳng AD là đường trung trực của đoạn thẳng BC.

Lý thuyết Tam giác cân. Đường trung trực của đoạn thẳng

1. Tam giác cân và tính chất

• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.

Ví dụ: Trong hình dưới đây, $Δ A B C$ có cạnh AB = AC được gọi là tam giác cân tại đỉnh A, hai cạnh AB và AC là hai cạnh bên, BC là cạnh đáy, $\hat{B}$ và $\hat{C}$ là hai góc ở đáy, $\hat{A}$ là góc ở đỉnh.

Lý thuyết Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng (ảnh 1)

• Tính chất:

+ Trong tam giác cân, hai góc ở đáy bằng nhau.

+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.

Ví dụ: Tam giác ABC cân tại A thì $\hat{B}$ = $\hat{C}$ . Ngược lại, tam giác ABC có $\hat{B}$ = $\hat{C}$ thì tam giác ABC cân tại A.

Lý thuyết Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng (ảnh 2)

Chú ý:

• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.

Ví dụ: Tam giác ABC có AB = AC = BC thì tam giác ABC được gọi là tam giác đều. Tam giác ABC đều có $\hat{A}$ = $\hat{B}$ = $\hat{C}$ = 60°.

Lý thuyết Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng (ảnh 3)

• Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.

• Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.

2. Đường trung trực của một đoạn thẳng

• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

Ví dụ: Đường thẳng d vuông góc với đoạn AB tại M và M là trung điểm của AB. Khi đó d được gọi là đường trung trực của đoạn thẳng AB.

Lý thuyết Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng (ảnh 4)

• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.

• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

Ví dụ: Đường thẳng d là đường trung trực của đoạn thẳng AB và D ∈ d.

Khi đó DA = DB.

Lý thuyết Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng (ảnh 5)

• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.

Chú ý:

• Cách vẽ đường trung trực của đoạn thẳng bằng compa và thước thẳng.

Chẳng hạn: Vẽ đường thẳng d là đường trung trực của đoạn thẳng AB như sau:

+ Vẽ đoạn thẳng AB;

+ Lấy A làm tâm, vẽ cung tròn (bán kính lớn hơn $\frac{A B}{2}$ ). Sau đó lấy B làm tâm, vẽ cung tròn cùng bán kính sao cho hai cung này cắt nhau tại hai điểm M và N;

+ Dùng thước thẳng vẽ đường thẳng đi qua M và N. Đường thẳng đó là đường trung trực của đoạn thẳng AB.

Lý thuyết Toán 7 Kết nối tri thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng (ảnh 6)