Tailieumoi.vn xin giới thiệu Bài tập chứng minh tam giác cân lớp 7 được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết chứng minh tam giác cân. Mời các bạn đón xem:
Bài tập chứng minh tam giác cân lớp 7
A. Bài tập chứng minh tam giác cân
1. Bài tập trắc nghiệm
Bài 1: Chọn câu sai
A. Tam giác đều có ba góc bằng nhau và bằng 60°
B. Tam giác đều có ba cạnh bằng nhau.
C. Tam giác cân là tam giác đều.
D. Tam giác đều là tam giác cân.
Lời giải:
Tam giác đều là tam giác có ba cạnh bằng nhau
Trong tam giác đều, mỗi góc bằng 60°
Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều
Chọn đáp án C.
Bài 2: Hai góc nhọn của tam giác vuông cân bằng
A. 30° B. 45° C. 60° D. 90°
Lời giải:
Mỗi góc nhọn của tam giác vuông cân bằng 45°
Chọn đáp án B.
Bài 3: Cho tam giác ABC cân tại A. Chọn phát biểu sai
Lời giải:
Chọn đáp án D.
Bài 4: Một tam giác cân có góc ở đỉnh là 64° thì số đo góc đáy bằng?
A. 54° B. 58° C. 72° D. 90°
Lời giải:
Góc ở đỉnh là 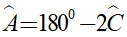
Áp dụng công thức số đo ở đáy là:
Chọn đáp án B.
Bài 5: Một tam giác cân có góc ở đáy bằng 70° thì góc ở đỉnh bằng bao nhiêu?
A. 64° B. 53° C. 70° D. 40°
Lời giải:
Góc ở đỉnh là 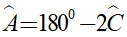
Áp dụng công thức số đo ở đỉnh là: 180° - 2.70° = 40°
Chọn đáp án D.
Bài 6: Cho tam giác ABC nhọn (không cân). Trên tia đối của tia AB lấy D sao cho AD = AC. Trên tia đối của tia AC lấy điểm E sao cho AE = AB. Chọn câu sai:
A. Tam giác ADC là tam giác cân
B. Tam giác ABE là tam giác cân
C. Tam giác ADE là tam giác cân
D. BC = DE
Lời giải:
Chọn đáp án C
Bài 7: Cho tam giác ABC cân tại A. Về phía ngoài tam giác ABC vẽ hai tam giác đều ACD và ABE. So sánh BD và CE.
A. BD = CE
B. BD > CE
C. BD < CE
D. BD = 2CE
Lời giải:
Chọn đáp án A
Bài 8: Cho tam giác MNP cân tại P có = 60°. Khi đó
A. Tam giác MNP vuông cân tại P
B. Tam giác MNP vuông cân tại M
C. Tam giác MNP là tam giác đều
D. Tam giác MNP là tam giác vuông tại P
Lời giải:
Ta có: tam giác MNP cân tại P có một góc = 60°
Suy ra tam giác MNP đều (dấu hiệu nhận biết tam giác đều)
Chọn đáp án C
Bài 9: Cho tam giác ABC cân tại A có = 2. Khi đó
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác vuông tại B
C. Tam giác ABC vuông cân tại A
D. Tam giác ABC vuông cân tại C
Lời giải:
Chọn đáp án C
Bài 10: Cho tam giác HIK đều có E là trung điểm của IK. Khi đó:
Lời giải:
Chọn đáp án B
2. Bài tập vận dụng
Bài 1: Câu nào đúng, câu nào sai? ( Đánh dấu x vào câu lựa chọn)
|
|
Đúng |
Sai |
|
a) Tam giác cân có một góc 45o là tam giác vuông cân. |
|
|
|
b) Mỗi góc ngoài của 1 tam giác thì bằng tổng 2 góc không kề nó của tam giác đó. |
|
|
|
c) Nếu tam giác có 1 cặp cạnh không bằng nhau thì tam giác đó không phải là tam giác cân. |
|
|
Bài 2: Cho tam giác ABC cân tại A, có . Tính các góc còn lại của tam giác đó.
Bài 3: Số tam giác cân ở hình sau là:
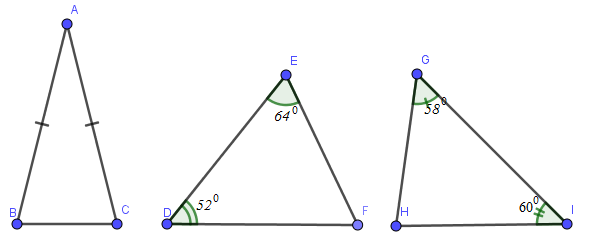
A. 0
B. 1
C. 2
D. 3
Bài 4: Cho ∆ABC cân tại A. Lấy điểm E và F lần lượt thuộc các cạnh AB, AC sao cho BE = CF. Chứng minh AEF là tam giác cân.
Bài 5: Vẽ tam giác đều ABC có AB = AC = BC = 6cm
Bài 6: Tìm các tam giác cân trên hình vẽ sau:
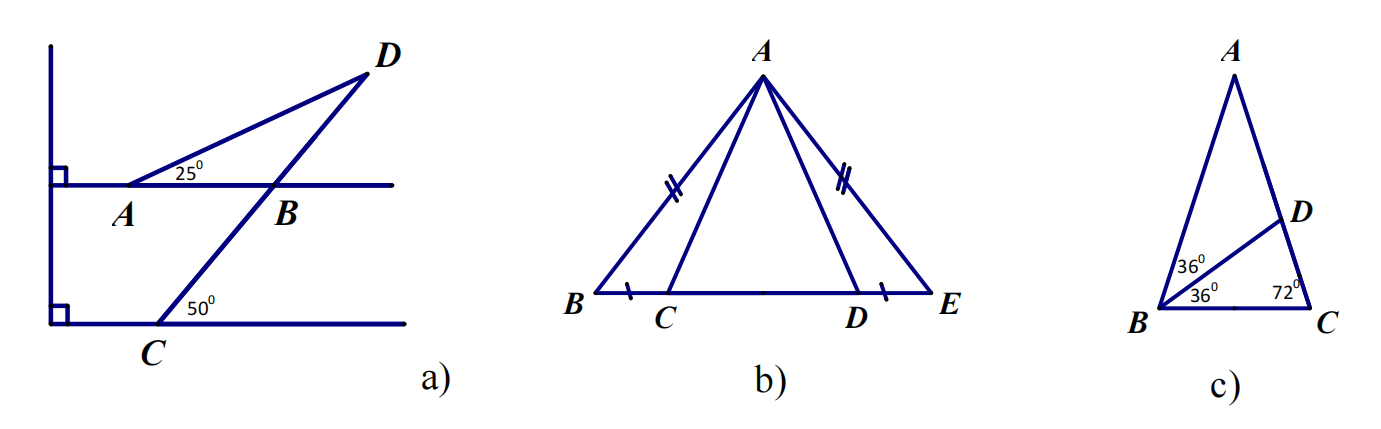
Bài 7: Hai đường cao BE và CF của tam giác ABC cắt nhau tại O. Biết OC = AB.
a) Chứng minh .
b) Tính góc ACB.
Bài 8: Tìm số đo x trên mỗi hình sau:
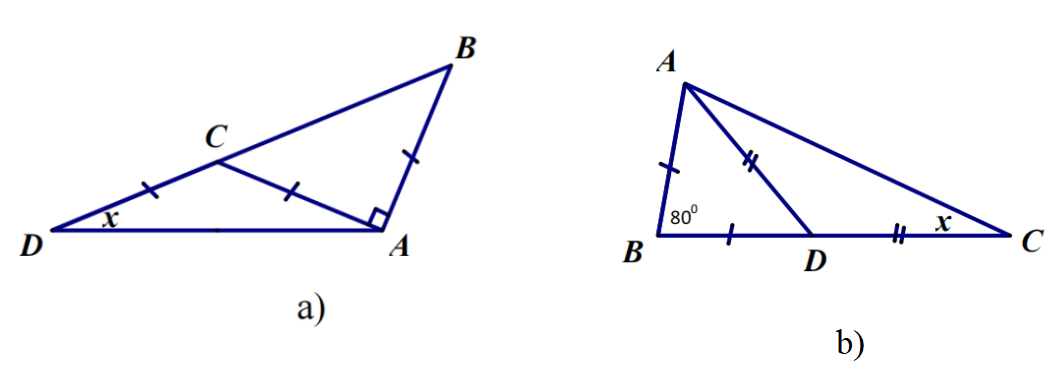
Bài 9: Cho cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK. Chứng minh và là các tam giác cân.
Bài 10: Cho điểm M thuộc đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC và BMD. Gọi E, F theo thứ tự là trung điểm của AD, CB. Chứng minh: MEF là tam giác đều.
3. Bài tập tự luyện
Bài 1. Trong các đáp án dưới đây đáp án nào sai?
A. Tam giác đều có ba góc bằng nhau và mỗi góc bằng 60°;
B. Tam giác đều là tam giác có ba cạnh bằng nhau;
C. Tam giác cân là tam giác đều;
D. Tam giác đều là tam giác cân đặc biệt.
Bài 2. Chọn đáp án đúng trong các đáp án sau, biết Tam giác ABC cân tại A, biết rằng số đo là 50o , vậy số đo các góc còn lại của tam giác ABC đã cho là:
A.
B.
C.
D.
Bài 3. Cho tam giác ABC cân, biết góc . Tính số đo của các góc còn lại của tam giác đó.
Bài 4. Cho tam giác ABC cân ở A. Trên cạnh BC lấy D, E sao cho BD = CE. Chứng minh tam giác ADE là tam giác cân.
Bài 5. Cho tam giác ABC có .
a) Chứng minh tam giác ABC cân.
b) Đường thẳng song song với BC cắt tia đối của tia AB ở D, cắt tia đối của tia AC ở E. Chứng minh tam giác ADE cân.
B. Lý thuyết Tam giác cân
Tam giác cân là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy.
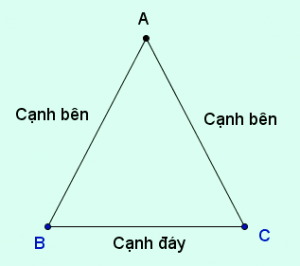
Ở hình trên, tam giác ABC có AB = AC suy ra tam giác ABC cân.
Có AB và AC là hai cạnh bên nên tam giác ABC cân tại đỉnh A.
2. Tính chất tam giác cân
Tam giác cân có 4 tính chất sau đây:
Tính chất 1: Trong một tam giác cân hai góc ở đáy bằng nhau.
Chứng minh:
| Giả thiết | Tam giác ABC cân tại A, AB = AC |
| Kết luận |
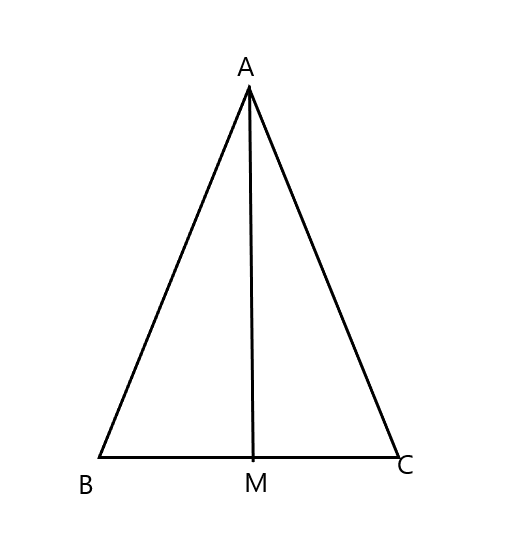
Trong tam giác cân ABC, gọi AM là tia phân giác của góc
Khi đó ta có
Xét tam giác ABM và tam giác ACM có:
AB = AC (gt)
(cmt)
AM chung
Suy ta ΔABM = ΔACM (c.g.c) (đpcm)
Tính chất 2: Một tam giác có hai góc bằng nhau thì là tam giác cân.
Chứng minh
| Giả thiết | Tam giác ABC, |
| Kết luận | Tam giác ABC cân tại A |
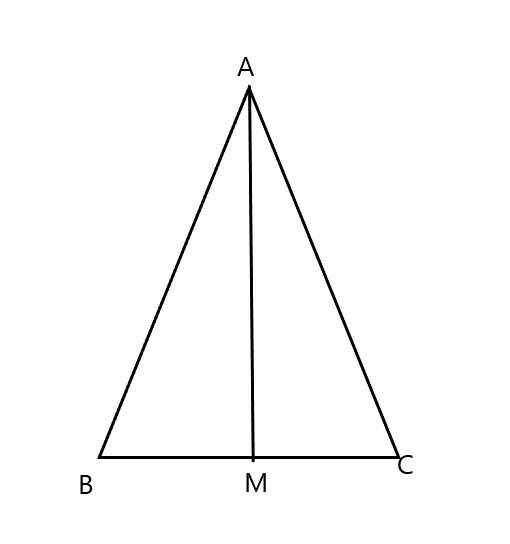
Trong tam giác ABC, gọi AM là tia phân giác của
Tam giác ABM có (tổng 3 góc trong một tam giác)
Tam giác ACM có (tổng 3 góc trong một tam giác)
Mà lại có
nên
Xét tam giác ABM và tam giác ACM có:
Suy ra ΔABM = ΔACM (g - g - g) nên AB = AC (cạnh tương ứng bằng nhau)
Xét tam giác ABC có AB = AC, suy ra tam giác ABC cân tại A (định nghĩa)
Tính chất 3: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường cao của tam giác đó.
Tính chất 4: Trong một tam giác, nếu có một đường trung tuyến đồng thời là đường trung trực thì tam giác là tam giác cân.
Trong tam giác cân có 2 dấu hiệu nhận biết đó là:
Dấu hiệu 1: Nếu một tam giác có hai cạnh bên bằng nhau thì tam giác đó là tam giác cân.
Dấu hiệu 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.
- Công thức tính diện tích tam giác cân: S = (a x h)/ 2
Trong đó:
– Cách 1: Chứng minh tam giác đó có hai cạnh bằng nhau.
– Cách 2: Chứng minh tam giác đó có hai góc bằng nhau.
Ví dụ 1: Trong tam giác ABC có Δ ABD = Δ ACD . Chứng minh tam giác ABC cân.
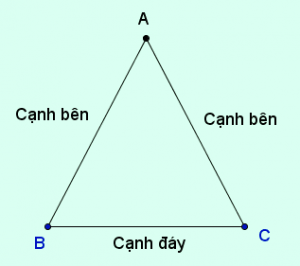
+ Chứng minh theo cách 1:
Theo bài ra, ta có:
Δ ABD = Δ ACD
=> AB = AC
=> Tam giác ABC cân tại A
+ Chứng minh theo cách 2:
Theo bài ra, ta có:
∆ ABD = ∆ ACD
=> Góc B = C
=> Tam giác ABC cân tại A
Ví dụ 2:
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE
a) So sánh góc ABD và ACE
b) Gọi I là giao điểm của BD và CE. ΔIBC là tam giác gì ? Vì sao ?
Gợi ý đáp án
a) Tam giác ABC cân tại A (giả thiết)
Xét ΔABD và ΔACE có:
AB = AC (giả thiết)
chung
AD = AE (giả thiết)
⇒ ΔABD = ΔACE (cạnh - góc - cạnh)
⇒ (cặp góc tương ứng)
b) ΔIBC có:
⇒ ΔIBC cân tại I
Ví dụ 3: Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
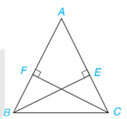
Gợi ý đáp án:
Do tam giác ABC cân tại A nên: (tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
BC chung
(cạnh huyền – góc nhọn)
=>BE=CF (2 cạnh tương ứng).
Ví dụ 4
Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Gợi ý đáp án:
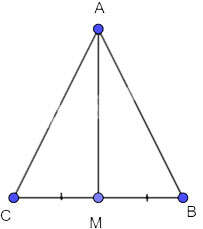
Xét 2 tam giác AMC và AMB có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
(2 góc tương ứng)
là phân giác của góc BAC
Mặt khác:(2 góc tương ứng) mà
(2 góc kề bù)
Nên: .
Vậy AM vuông góc với BC.
Ví dụ 5
Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
Gợi ý đáp án:
a)
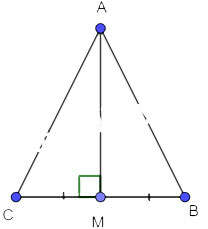
Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=> AM=BM (2 cạnh tương ứng)
=> Tam giác ABM cân tại A
b)
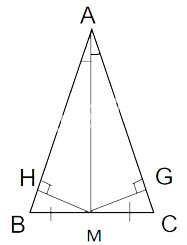
Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGC có:
AM chung
(cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM(gt)
MH=MG(cmt)
(cạnh huyền – cạnh góc vuông)
(2 góc tương ứng)
=>Tam giác ABC cân tại A.
Ví dụ 6
Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45°;
c) Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
Gợi ý đáp án:
a) Do tổng ba góc trong 1 tam giác bằng 180 độ nên tam giác không thể có 2 góc vuông
=>Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau
=> Tam giác vuông cân thì cân tại đỉnh góc vuông.
b) Giả sử hai góc nhọn trong tam giác vuông là x, ta có:
Vậy tam giác vuông cân có hai góc nhọn bằng 45°.
c) Gọi góc còn lại của tam giác vuông có 1 góc nhọn bằng 45° là x, ta có:
Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
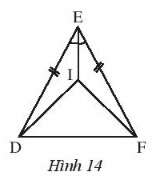
Ví dụ 7Cho hình 14, biết ED = EF và EI là tia phân giác của.
Chứng minh rằng:
a.
b. Tam giác DIF cân.
Gợi ý đáp án:
a. Xét và
có:
EI chung
DE = EF.
b. Vì (chứng minh trên)
Tam giác DIF cân tại I.
Cho tam giác ABC cân tại A có
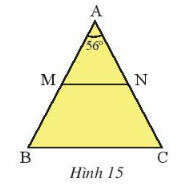
a. Tính .
b. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh tam giác AMN cân.
c. Chứng minh rằng MN // BC.
Gợi ý đáp án:
a. Vì tam giác ABC cân tại A
b. Vì M, N lần lượt là trung điểm của AB, AC nên
mà AB = AC ( vì cân)
Tam giác AMN cân tại A.
c. Xét cân tại A có:
Xét cân tại A có:
Mà 2 góc này ở vị trí đồng vị
.
C. Các dạng bài tập cơ bản
Dạng 1: Cách vẽ tam giác cân, vuông cân, tam giác đều
1. Phương pháp giải:
Dựa vào các cách vẽ tam giác đã học và định nghĩa các tam giác cân, vuông cân, đều.
2. Ví dụ minh họa:
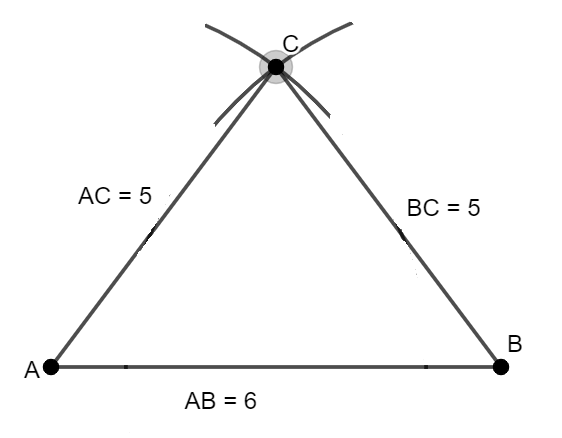
Ví dụ 1: Vẽ tam giác ABC cân tại C có AB = 6 cm, AC = BC = 5cm.
Giải: (Vẽ tương tự như cách vẽ tam giác thường biết độ dài ba cạnh)
Cách vẽ:
- Vẽ đoạn thẳng AB = 6cm.
- Vẽ cung tròn tâm A bán kính 5cm.
- Vẽ cung tròn tâm B bán kính 5cm.
- Hai cung tròn này cắt nhau tại C.
- Nối CA, CB ta được tam giác ABC cần vẽ.
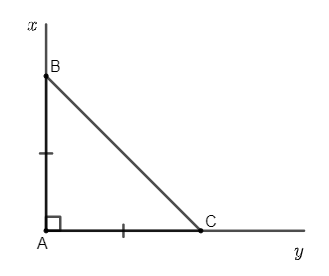
Ví dụ 2: Vẽ tam giác ABC vuông cân tại A.
Giải:
- Vẽ góc vuông xAy
- Trên tia Ax lấy điểm B, trên tia Ay lấy điểm C sao cho AB = AC
- Nối B với C
- Khi đó ta được tam giác ABC vuông cân tại A.
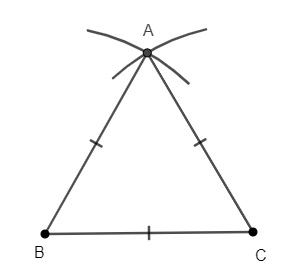
Ví dụ 3: Vẽ tam giác đều ABC có cạnh bằng 4 cm.
Giải:
- Vẽ đoạn thẳng BC = 4 cm
- Vẽ cung tròn tâm B bán kính 4 cm.
- Vẽ cung tròn tâm C bán kính 4 cm.
- Hai cung tròn này cắt nhau tại A.
- Nối AB, AC ta được tam giác ABC cần vẽ.
Dạng 2: Nhận biết một tam giác là tam giác cân, vuông cân, đều
1. Phương pháp giải:
Những dấu hiệu nhận biết các tam giác cân, vuông cân, đều:
*Tam giác cân:
- Tam giác cân là tam giác có hai cạnh bằng nhau (theo định nghĩa).
- Tam giác có hai góc bằng nhau là tam giác cân.
*Tam giác vuông cân:
- Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau (theo định nghĩa).
- Tam giác vuông có một góc nhọn bằng 45o là tam giác vuông cân.
*Tam giác đều:
- Tam giác đều là tam giác có ba cạnh bằng nhau (theo định nghĩa).
- Tam giác có ba góc bằng nhau là tam giác đều.
- Tam giác cân có một góc bằng 60° là tam giác đều.
2. Ví dụ minh họa:
Ví dụ 4: Tìm các tam giác cân, vuông cân, đều trên hình vẽ sau:
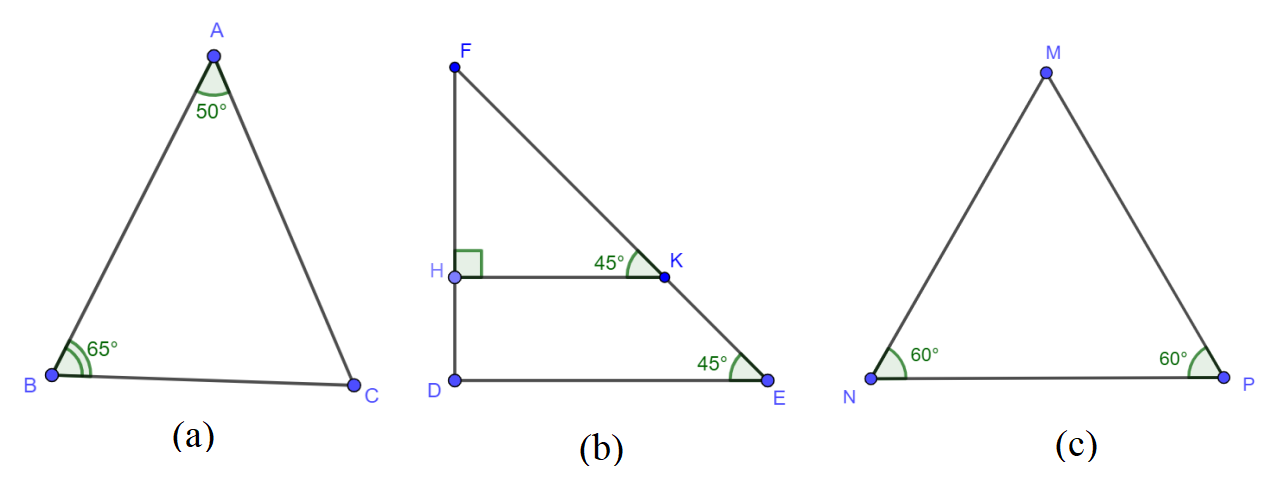
Giải:
(a) Áp dụng định lý góc ngoài trong tam giác ABC có:
có
Do đó cân tại A.
(b) Ta có, vuông tại H có
Nên là tam giác vuông cân tại H (1)
Vì
Mà hai góc này ở vị trí so le trong nên HK // DE
Vì , HK // DE
(Tính chất từ vuông góc đến song song)
Ta có, vuông tại D có
Nên là tam giác vuông cân tại D (2)
Từ (1) và (2) suy ra , là tam giác vuông cân.
(c) Áp dụng định lý tổng ba góc trong tam giác MNP có:
Ta có, có
Do đó là tam giác đều.
Dạng 3: Sử dụng định nghĩa, tính chất tam giác cân, vuông cân, đều để suy ra các đoạn thẳng, các góc bằng nhau
1. Phương pháp giải: Dựa vào định nghĩa và tính chất của tam giác cân, vuông cân, đều.
2. Ví dụ minh họa:
Ví dụ 5: Cho tam giác ABC cân tại A (BC < AB). Trên cạnh AB lấy D sao cho CD = CB.
a) Chứng minh: .
b) Trên tia đối của tia CA lấy E sao cho CE = AD. Chứng minh BE = BA.
Giải:
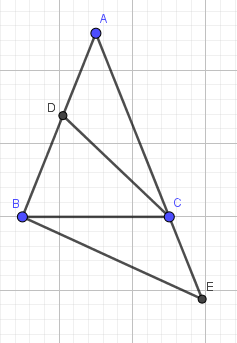
|
GT |
Cho , AB = AC (BC < AB) CD = CB (D CE là tia đối của tia CA: CE = AD |
|
KL |
a) b) BE = BA |
a) cân tại A nên
Vì cân tại C (do CD = CB) nên
Từ (1) và (2) suy ra
b) Ta có:
Mà (câu a)
Do đó:
Xét và có:
CE = AD (gt)
(cmt)
CD = CB (gt)
Do đó:
(hai cạnh tương ứng)
Mà AC = AB (do tam giác ABC cân tại A)
Vậy BE = AB (đpcm).
Dạng 4: Tính độ dài đoạn thẳng, tính số đo góc
1. Phương pháp giải:
Dựa vào định lý tổng ba góc của một tam giác và mối quan hệ giữa các cạnh, các góc trong tam giác đó.
2. Ví dụ minh họa:
Ví dụ 6: Cho tam giác ABC cân tại A và tam giác đều BCD (D và A nằm khác phía đối với BC). Tính số đo góc BDA.
Giải:
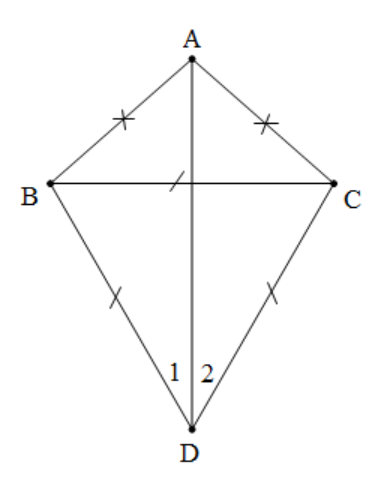
|
GT |
(D và A nằm khác phía đối với BC) |
|
KL |
|
Xét và có:
AB = AC ( cân)
BD = CD ( đều)
Cạnh AD chung
Do đó:
(hai góc tương ứng)
Mặt khác, đều nên
Vậy .